[学习笔记]多项式
FFT
前言
关于多项式乘法,朴素时间复杂度是 \(O(n^2)\) 的,我们考虑优化
我们发现,如果将多项式转为点值表示法后,相乘是 \(O(n)\) 的
于是我们将问题转化为了如何实现系数表示法与点值表示法间的互相转化
我们发现转化之间的复杂度也是 \(O(n^2)\) 的(秦九韶算法 & Lagrange插值)
所以我们考虑优化
优化--系数 \(\rightarrow\) 点值
前置知识
高中数学(复数)
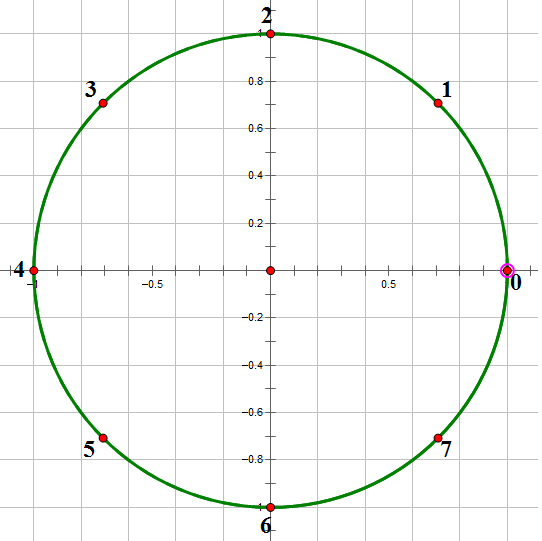
首先介绍一下单位根:
在复平面上画一个以(0,0)为圆心的单位圆,将该圆n等分
规定(1,0)为第零个等分点,逆时针标号,就得到了第0n-1个等分点,也就是第0n-1
个n次单位根,记做\(\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}\)
如八次单位根:(\(\omega_n^0,\omega_n^1,\cdots,\omega_n^7\)的标号为\(1,2,\cdots,7\))
然后是几个性质与证明
-
\(\omega_n^k=e^\frac{2\pi ik}{n}\)
根据欧拉公式 \(e^{i\theta}=cos\theta+i*sin\theta\) 可得
-
\(\omega_{dn}^{dk}=\omega_n^k\)
\(\omega_{dn}^{dk}=e^\frac{2\pi idk}{dn}=e^\frac{2\pi ik}{n}=\omega_n^k\)
-
设 \(\omega_n^k=a+bi\) ,则 \(\omega_n^{-k}=a-bi\)
将 \(\omega_n^k=e^\frac{2\pi ik}{n}\) 带入即可证明
-
\(\omega_n^{k+\frac n2}=-\omega_n^k\)
\(\omega_n^{k+\frac n2}=\omega_n^k*\omega_n^\frac n2=-\omega_n^k\)
DFT
嗯,终于到正文了
DFT主要的思想是在求一部分值的时候求出来另外一部分,分治进行
比如我们现在要把多项式 \(A(x)=\displaystyle\sum_{i=0}^na_ix^i\) 在
\(x_1,x_2,\cdots,x_n\) 处的取值求出
我们考虑将 A 的系数按照下标的奇偶性分类,即
\(\displaystyle A_0(x)=a_0+a_2x^1+a_4x^2+\cdots, A_1(x)=a_1+a_3x^1+a_5x^2+\cdots\)
所以 \(A(x)=A_0(x^2)+x*A_1(x^2)\)
我们考虑分别将 \(\omega_n^k\) 与 \(\omega_n^{k+\frac n2}\) 带入
就可得:
\(\begin{cases}A(\omega_n^k)&=&A_0(\omega_n^{2k})+\omega_n^kA_1(\omega_n^k)\\A(\omega_n^{
k+\frac n2})&=&A_0(\omega_n^{2k})-\omega_n^kA_1(\omega_n^{2k})\end{cases}\)
我们发现 \(A_1\) 项只有常数项不同,所以我们可以仅递归计算每一个 k 的
\(A_0(\omega_n^k),A_1(\omega_n^k)\) ,并用这两项计算出 \(A(\omega_n^k)\) 与
\(A(\omega_n^{k+\frac n2})\)
这样我们就将问题规模缩减了一半
所以时间复杂度是 \(T(n)=2T(\dfrac n2)+O(n)=O(n\log n)\) 的
优化--点值 \(\rightarrow\) 系数
前置知识
-
前面所有
-
矩阵
IDFT
现在我们可以用 DFT 将系数表示为点值,那么我们还需要用同样优秀的复杂度变回去
这就需要 IDFT 了
首先在介绍一个单位根的性质: \(\displaystyle\dfrac1n\sum_{i=0}^{n- 1}\omega_n^{v*i}=[v\%n==0]\)
证明:
你发现 \(\omega_n^{v*i}=\omega_n^{v*(i-1)}*\omega_n^v\)
所以 \({\omega_n^{v*i}}\) 是个等比数列
-
\(v\%n=0\)
\(\displaystyle\sum_{i=0}^{n-1}\omega_n^{v*i}=\sum_{i=0}^{n-1} 1^i=n\)
-
\(v\%n\not=0\)
根据等比数列求和公式,\(\displaystyle\sum_{i=0}^{n-1}\omega_n^{v*i}=\dfrac{1-\omega_n^{n*v}}{1-\omega_n^v}=\dfrac{1-1^v}{1-\omega_n^v}=0\)
证毕
然后来推下式子(单位根反演登场):
假设我们要求 \(c=a*b\):
\(\displaystyle{\begin{aligned}c_i=&\sum_{j=0}^ia_j\times b_{i-j}\\c_i=&\sum_{p=0}\sum_{q=0}a_p\times b_q[(p+q)\%n=0]\\nc_i=&\sum_{p=0}\sum_{q=0}a_p\times b_q\sum_{j=0}\omega_n^{(p+q-i)j}\\nc_i=&\sum_{j=0}\omega_n^{(-i)j}(\sum_{p=0}\omega_n^{pj}a_p)(\sum_{q=0}\omega_n^{qj}b_q)\end{aligned}}\)
我们设 \(f_a(j)=\sum_{i=0}\omega_n^{ij}a_i\ ,\ f_a^{-1}(j)=\sum_{i=0}\omega_n^{(-i)j}a_i\)
则
\(\displaystyle{\begin{aligned}nc_i=&\sum_{j=0}\omega_n^{(-i)j}f_a(j)f_b(j)\\nc_i=&\sum_{j=0}\omega_n^{(-i)j}f_c(j)\\nc_i=&f_{f_c}^{-1}(i)\end{aligned}}\)
而我们发现, \(f_a(j)\) 就是多项式 \(a\) 在 \(\omega_n^j\) 处的点值,也就是说
\(f_a\) 就是 a 在 DFT 后的结果
所以 \(f_a^{-1}\) 就是我们的 IDFT
所以我们发现 IDFT 的过程其实和 DFT 的过程极为相似,但有两点不同
-
带入的值从 \(\omega_n^j\) 变为 \(\omega_n^{-j}\)
-
在最后要将所有的 \(f_{f_c}^{-1}(i)\) 除以 n 才是真正的 \(c_i\)
算法到这里就结束啦!
小优化
我们发现在递归时,我们会浪费很多时间
考虑我们递归的原因,是为了将系数奇偶分类,偶在前,奇在后
那么如果我们提前模拟将系数全部分好类,再用 for 循环代替递归,就可以节省很多时间复杂度
有一个性质:最后的序列其实就是原序列二进制反转了一下
如图:

考虑我们在第 i 次分组时,参照的是二进制第 i 位的奇偶,确定的是位置的二进制第 (len-i+1) 位(也就是 0 向左,1 向右),刚好奇偶性相同
所以就有了上面的性质
现在我们可以 \(O(n)\) 的完成奇偶分类,所以现在我们可以通过非递归快速实现了
\(\mathcal{Talk\ is\ cheap,show\ you\ the\ Code:}\)
const double PI=acos(-1.0);
struct Complex{//复数结构体
double x,y;
Complex(double _x=0.0,double _y=0.0){x=_x;y=_y;}
Complex operator - (const Complex &b)const{return Complex(x-b.x,y-b.y);}
Complex operator + (const Complex &b)const{return Complex(x+b.x,y+b.y);}
Complex operator * (const Complex &b)const{return Complex(x*b.x-y*b.y,x*b.y+y*b.x);}
}x1[N],x2[N];
inline void change(Complex y[],int len){//二进制反转
int i,j,k;
for(i=1,j=len/2;i<len-1;i++){
if(i<j) swap(y[i],y[j]);
k=len/2;
while(j>=k) j=j-k;k=k/2;//模拟减法的进位
j+=k;//进位
}
}
inline void FFT(Complex y[],int len,int on){//on 在 1 时是 DFT,-1 时是IDFT
change(y,len);
for(int h=1;h<=len;h<<=1){//模拟递归
Complex wn(cos(2*PI/h),sin(on*2*PI/h));//注意在递归时每次自变量会平方
for(int j=0;j<len;j+=h){
Complex w(1,0);
for(int k=j;k<j+h/2;k++){
Complex u=y[k];
Complex t=w*y[k+h/2];
y[k]=u+t;y[k+h/2]=u-t;
w=w*wn;
}
}
}
if(on==-1){
for(int i=0;i<len;i++) y[i].x/=len;
}
}
int str1[N],str2[N],sum[N];
signed main(){
int len1=read()+1,len2=read()+1,len=1;
for(int i=0;i<len1;i++) str1[i]=read();
for(int i=0;i<len2;i++) str2[i]=read();
while(len<=(len1+len2)) len<<=1;//注意我在递归进行时,每次lim会减半,中点两侧的值都需要计算。所以我把lim变为2的整次幂,方便递归与计算
for(int i=0;i<len1;i++) x1[i]=Complex(str1[i],0);
for(int i=0;i<len2;i++) x2[i]=Complex(str2[i],0);
FFT(x1,len,1);FFT(x2,len,1);
for(int i=0;i<len;i++) x1[i]=x1[i]*x2[i];
FFT(x1,len,-1);
for(int i=0;i<len;i++) sum[i]=(int)(x1[i].x+0.5);
len=len1+len2-1;
// while(sum[len]==0&&len>0) len--;
for(int i=0;i<len;i++) cout<<sum[i]<<" ";
cout<<"\n";
}
NTT
在某些时候,我们需要求模 p 意义下的卷积
前置知识
-
阶
如果 \(\gcd(a,p)=1\),那么对于方程 \(a^r\equiv1\pmod p\) 来说,根据欧拉定理 \(a^{\varphi(p)}\equiv1\pmod p\),一定存在解 \(r|\varphi(p)\)
最小的 r 称为 a 关于 p 的阶,记作 \(ord_p(a)\)
求阶只能从小到大枚举
-
原根
在模 p 意义下的 0~p-1 次幂各不相同,取遍 [0,p-1],也就是说 \(ord_p(g)=\varphi(p)\) (p为质数)
关于原根的几个性质:
-
注意到所有的素数都有原根
-
当正整数 p 有原根时,原根的个数为 \(\varphi(\varphi(p))\)
-
令 p 的原根是 g,那么 \(g,g^2,\cdots,g^{\varphi(p)}\) 构成了模 p 简化剩余系
-
实现
先求出 p 的原根 g,方法如下
从小到大枚举 \(d\in [2,p-1]\),令 \(a_i\) 为 \(\varphi(p)\) 的素因子,若 \(d^{\frac{\varphi(p)}{a_i}}\equiv1\pmod p\) 都不成立,那么 d 就是模 p 的一个原根
这种方法的证明:
假设对于 \(d^{\frac{\varphi(p)}{a_i}}\equiv1\pmod p\) 均不成立,但存在 \(k<\varphi(p)\),使得 \(dk\equiv1\pmod p\)
令 \(q=\gcd(k,\varphi(p))\),那么 q<p 并且 x 一定整除 \(\dfrac{\varphi(p)}{a_i}\) 中的一个,不妨设它整除 \(\dfrac{\varphi(p)}{a_i}\)
考虑等式 \(kn+\varphi(p)m=q\),容易发现一定存在正整数解
由于 \(d^q\equiv d^{kn+φ(p)m}≡1\pmod p\),而 \(q|\dfrac{\varphi(p)}{a_i}\),与假设矛盾
得证
在求出原根后,可以发现,\(g^\frac{p-1}n\) 与 \(w_n\) 的性质类似
所以我们可以用 \(g^\frac{p-1}n\) 来代替 \(w_n\)
和FFT几乎相同
PS:这种方法只在 \(p=a*2^k+1\) 的情况下才成立
关于任意模数 NTT:不会写
三模数 NTT
首先挑选 3 个 \(a*2^k+1\) 形式的模数,进行3次 NTT,求出3组答案
然后将每一个数用中国剩余定理合并即可
inline void NTT(int y[],int len,int on){
Change(y,len);
for(int h=1,mul,u,t;h<=len;h<<=1){
if(on==1) mul=ksm(G,(mod-1)/h);
else mul=ksm(Ginv,(mod-1)/h);
for(int j=0,w;j<len;j+=h){
w=1;
for(int k=j;k<j+(h>>1);k++){
u=y[k];t=(w*y[k+(h>>1)])%mod;
y[k]=(u+t)%mod;y[k+(h>>1)]=(u-t+mod)%mod;
w=(w*mul)%mod;
}
}
}
if(on==-1){
int mul=ksm(len,mod-2);
for(int i=0;i<len;i++) y[i]=(y[i]*mul)%mod;
}
}
另外附一张 long long 以内的 NTT 模数原根表(其中 \(g\) 是 \(p=r\times2^k+1\) 的原根):
| p | r | k | g |
|---|---|---|---|
| 3 | 1 | 1 | 2 |
| 5 | 1 | 2 | 2 |
| 17 | 1 | 4 | 3 |
| 97 | 3 | 5 | 5 |
| 193 | 3 | 6 | 5 |
| 257 | 1 | 8 | 3 |
| 7681 | 15 | 9 | 17 |
| 12289 | 3 | 12 | 11 |
| 40961 | 5 | 13 | 3 |
| 65537 | 1 | 16 | 3 |
| 786433 | 3 | 18 | 10 |
| 5767169 | 11 | 19 | 3 |
| 7340033 | 7 | 20 | 3 |
| 23068673 | 11 | 21 | 3 |
| 104857601 | 25 | 22 | 3 |
| 167772161 | 5 | 25 | 3 |
| 469762049 | 7 | 26 | 3 |
| 1004535809 | 479 | 21 | 3 |
| 2013265921 | 15 | 27 | 31 |
| 2281701377 | 17 | 27 | 3 |
| 3221225473 | 3 | 30 | 5 |
| 75161927681 | 35 | 31 | 3 |
| 77309411329 | 9 | 33 | 7 |
| 206158430209 | 3 | 36 | 22 |
| 2061584302081 | 15 | 37 | 7 |
| 2748779069441 | 5 | 39 | 3 |
| 6597069766657 | 3 | 41 | 5 |
| 39582418599937 | 9 | 42 | 5 |
| 79164837199873 | 9 | 43 | 5 |
| 263882790666241 | 15 | 44 | 7 |
| 1231453023109121 | 35 | 45 | 3 |
| 1337006139375617 | 19 | 46 | 3 |
| 3799912185593857 | 27 | 47 | 5 |
| 4222124650659841 | 15 | 48 | 19 |
| 7881299347898369 | 7 | 50 | 6 |
| 31525197391593473 | 7 | 52 | 3 |
| 180143985094819841 | 5 | 55 | 6 |
| 1945555039024054273 | 27 | 56 | 5 |
| 4179340454199820289 | 29 | 57 | 3 |
多项式求逆
主要思想是递归处理,每次减半
首先我们在 \(\mod x^{n}\) 处的逆元可以费马小定理直接求
现在假设我们现在求出来了 \(F*G\equiv1\pmod {x^{\lceil\frac n2\rceil}}\) , 要
求 \(F*G'\equiv 0\pmod {x^n}\)
那么
\(\begin{aligned}G'&\equiv G&&\pmod {x^{\lceil\frac n2\rceil}}\\(G'-G)^2&\equiv0&&\pmod {x^n}\\F*(G'-G)^2&\equiv0&&\pmod {x^n}\\F*G'^2-2F*G*G'+F*G^2&\equiv0&&\pmod {x^n}\\G'-2G+F*G^2&\equiv0&&\pmod {x^n}\\G'&\equiv 2G-F*G^2&&\pmod {x^n}\end{aligned}\)
那么现在我们就可以 \(O(n\log n)\) 的时间递归求逆了
void INV(int x[],int inv[],int len){
if(len==1){inv[0]=ksm(x[0],mod-2);return ;}
INV(x,inv,(len+1)>>1);
int lim=1;
while(lim<(len<<1)) lim<<=1;
for(int i=0;i<len;i++) c[i]=x[i];
for(int i=len;i<lim;i++) c[i]=0;//一定要注意各种清空
NTT(c,lim,1);NTT(inv,lim,1);
for(int i=0;i<lim;i++) inv[i]=(inv[i]*((2-c[i]*inv[i]%mod)%mod+mod)%mod)%mod;
NTT(inv,lim,-1);
for(int i=len;i<lim;i++) inv[i]=0;//一定要注意各种清空
}
多项式求ln
前置知识:求导(高中数学)
假设我们现在有多项式 \(G\),需要求 \(LN\equiv ln(G)\pmod{x^n}\)
由于多项式的求导、求积可以以 \(O(n)\) 的时间复杂度方便的做到,所以考虑对等式
两侧同时求导
那么
\(\begin{aligned}LN&\equiv ln(G)&&\pmod{x^n}\\LN'&\equiv \dfrac{G'}{G}&&\pmod{x^n}\\\end{aligned}\)
对于\(\dfrac1{G}\),我们通过多项式求逆 \(O(n\log n)\) 解决
对于\(G'\),我们可以 \(O(n)\) 解决
相乘,再求积即可
void LN(int x[],int ln[],int len){
if(len==1){ln[0]=0;return ;}
INV(x,ln,len);
int lim=1;
while(lim<(len<<1)) lim<<=1;
for(int i=0;i<len-1;i++) d[i]=(x[i+1]*(i+1))%mod;
for(int i=len-1;i<lim;i++) d[i]=0;
NTT(ln,lim,1);NTT(d,lim,1);
for(int i=0;i<lim;i++) ln[i]=(ln[i]*d[i])%mod;
NTT(ln,lim,-1);
for(int i=lim-1;i>=0;i--) ln[i+1]=ln[i]*ksm(i+1,mod-2)%mod;
ln[0]=0;
}
多项式求exp
前置知识
-
泰勒展开
\(\displaystyle f(x)=\sum_{i=0}^{\infty}\dfrac{f^{(i)}(x_0)}{i!}(x-x_0)^i\) ,其中 \(x\rightarrow x_0\)
主要用于将一个函数表示为多项式形式
由于 \(x\rightarrow x_0\) ,所以 \(\dfrac{f^{(i)}(x_0)}{i!}(x-x_0)^i\rightarrow 0\)
因此有时可以将 f(x) 近似为 \(\displaystyle\sum_{i=0}^n\dfrac{f^{(i)}(x_0)}{i!}(x-x_0)^i\) -
牛顿迭代
给定一个多项式函数 F(X),求一个多项式 X 使得 \(F(X)\equiv0\pmod{x^n}\)
假设已经迭代得到 \(F( X_0)\equiv0\pmod{x^{\lceil\frac n2\rceil}}\),考虑将 \(F(X)\) 在 \(X_0\) 处展开,那么 \(\begin{aligned}\sum_{i=0}^n\dfrac{F^{(i)}(X_0)}{i!}(X-X_0)^i&\equiv0&&\pmod{x^n}\end{aligned}\)
发现当 i>1 时,有 \((X-X_0)^i\equiv0\pmod{x^n}\)
所以有
\(\begin{aligned}F(X_0)+F'(X_0)(X-X_0)&\equiv0&&\pmod{x^n}\\X&\equiv X_0-\dfrac{F(X_0)}{F'(X_0)}&&\pmod{x^n}\end{aligned}\)
假设我们现在有多项式 G,需要求 \(X\equiv e^G\pmod{x^n}\)
变形可得
\(\begin{aligned}ln(X)-G&\equiv0&&\pmod{x^n}\end{aligned}\)
设 \(F(X)=ln(X)-G\),代入牛顿迭代,得
\(\begin{aligned}X&\equiv X_0-\dfrac{ln(X_0)-G}{\dfrac{1}{X_0}}&&\pmod{x^n}\\X&\equiv X_0-ln(X_0)*X_0-GX_0&&\pmod{x^n}\end{aligned}\)
void EXP(int x[],int exp[],int len){
if(len==1){
exp[0]=1;return ;
}
EXP(x,exp,(len+1)>>1);
LN(exp,e,len);
int lim=1;
while(lim<(len<<1)) lim<<=1;
for(int i=0;i<len;i++) e[i]=((x[i]-e[i]+(i==0))%mod+mod)%mod;
for(int i=len;i<lim;i++) e[i]=0;
NTT(exp,lim,1);NTT(e,lim,1);
for(int i=0;i<lim;i++) exp[i]=(exp[i]*e[i])%mod;
NTT(exp,lim,-1);
for(int i=len;i<lim;i++) exp[i]=0;
for(int i=0;i<lim;i++) e[i]=0;
}
多项式快速幂
先求 ln,再数乘,最后 exp 即可
inline void KSM(int x[],int y,int ans[],int len){
int lim=1;
while(lim<(len<<1)) lim<<=1;
LN(x,ans,len);
for(int i=0;i<lim;i++){x[i]=(ans[i]*y)%mod;ans[i]=0;}
EXP(x,ans,len);
}
分治NTT
假设有一个形式为 \(f[i]=\displaystyle\sum_{j=1}^if[i-j]g[j]\)
它显然不是卷积,但是差别仅在于等号的右侧也出现了 f
处理方法类似 CDQ 分治
假设现在已经求出了 \(f(0)\) 到 \(f(\frac n2)\),要计算它们对未知部分 \(f(\frac n2+1)\) 到 \(f(n)\) 的贡献
发现一个已知的 f(x),对任意一个 f(i)(i>x) 的贡献都只有 f(x)g(i-x)
于是贡献函数 F 就长这样了:
\(F(x)=\sum_{i=1}^xf(i)g(x-i)\)
其中 f 只填充 \([l,mid]\) 的部分,因为其他地方的 f=0
g 只填充 \([1,r-l]\) 的部分,因为只算对于 \([mid,r]\) 的贡献
void CDQ(int l,int r){
if(l==r) return ;
int mid=(l+r)>>1;
CDQ(l,mid);
for(int i=0;i<r-l+1;i++) A[i]=B[i]=0;
for(int i=l;i<=mid;i++) A[i-l]=f[i];
for(int i=1;i<r-l+1;i++) B[i]=g[i];
NTT(A,r-l+1,1);NTT(B,r-l+1,1);
for(int i=0;i<r-l+1;i++) A[i]=(A[i]*B[i])%mod;
NTT(A,r-l+1,-1);
for(int i=mid+1;i<=r;i++) f[i]=(f[i]+A[i-l])%mod;
CDQ(mid+1,r);
}
signed main(){
while(lim<n) lim<<=1;//先扩展为2^x的形式,方便处理
CDQ(0,lim-1);
}


