Pyhton环境与基础训练
（一）、练习安装Python解释器
【实验截图】
下载完python，IDLE运行正常
（二）、练习搭建Python+Eclipse+pydev编程环境
【实验截图】
在Eclipse 中安装pydev插件
安装完成后，打开首选项，出现PyDev
开始配置pydev解释器
（三）、练习安装Python扩展库
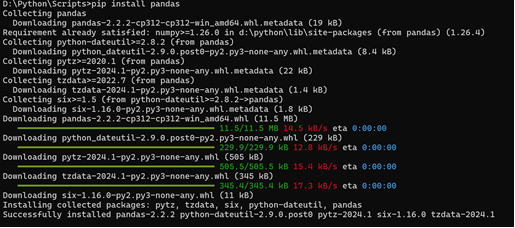
（四）、【Python0002】排列组合序列
【题目描述】
用户输入整数n（1<=n<=26）和整数m（m<=n），然后输入n个不同的字母，请编写程序输出在这n个字母中选择m个字母的所有排列序列和组合序列。
【源代码程序】
import itertools
num=input().split(" ")
num1=int(num[1])
arr = input().split(" ")
print(arr)
a = list(itertools.combinations(arr,num1))
b = list(itertools.permutations(arr,num1))
print("Permutation:" )
for i in b:
for j in i:
print(j,end=" ")
print()
print("Combination:" )
for i in a:
for j in i:
print(j,end=" ")
print()
【运行测试】
（五）、【Python0003】蒙特·卡罗法计算圆周率
【题目描述】
蒙特·卡罗方法是一种通过概率来得到问题近似解的方法，在很多领域都有重要的应用，其中就包括圆周率近似值的计问题。假设有一块边长为2的正方形木板，上面画一个单位圆，然后随意往木板上扔飞镖，落点坐标(x,y)必然在木板上（更多的时候是落在单位圆内），如果扔的次数足够多，那么落在单位圆内的次数除以总次数再乘以4，这个数字会无限逼近圆周率的值。这就是蒙特·卡罗发明的用于计算圆周率近似值的方法。编写程序，模拟蒙特·卡罗计算圆周率近似值的方法，输入掷飞镖次数，然后输出圆周率近似值。
【源代码程序】
import random
#使用扩展库 random
num=int(input())
ok=0
for i in range(1,num+1):
x=random.uniform(-1,1)#到-1到1的随机数
y=random.uniform(-1,1)
if(x*x+y*y<=1):
ok+=1
print(ok/num*4)
【运行测试】
（六）、【Python0004】验证6174猜想
【题目描述】
1955年，卡普耶卡(D.R.Kaprekar)对4位数字进行了研究，发现一个规律：对任意各位数字不相同的4位数，使用各位数字能组成的最大数减去能组成的最小数，对得到的差重复这个操作，最终会得到6174这个数字，并且这个操作最多不会超过7次。请编写程序验证这个猜想。
【源代码程序】
def Min_Number(a):
a=str(a)
arr=[]
for i in range(0,4):
arr.append(a[i])
arr.sort()
return int(''.join(arr))
def Max_Number(a):
a=str(a)
arr = []
for i in range(0, 4):
arr.append(a[i])
arr.sort(reverse=True)
return int(''.join(arr))
a=input()
while (int(a)!=6174):
a=Max_Number(a)-Min_Number(a)
print(a,end=" ")
【运行测试】
（七）、【Python0005】模拟页面调度LRU算法
【题目描述】
所谓LRU算法，是指在发生缺页并且没有空闲主存块时，把最近最少使用的页面换出主存块，腾出地方来调入新页面。
问题描述：一进程获得n个主存块的使用权，对于给定的进程访问页面次序，问当采用LRU算法时，输出发生的缺页次数。
【源代码程序】
def LRU(pages, maxNum,n):
temp = []
times = 0
for page in lst:
num = len(temp)
if num < n:
times += 1
temp.append(page)
elif num == n: #要访问的新页面已在主存块中
if page in temp: #处理“主存块”，把最新访问的页面交换到列表尾部
pos = temp.index(page)
temp = temp[:pos] + temp[pos+1:] + [page]
else: #把最早访问的页面踢掉，调入新页面
temp.pop(0)
temp.append(page)
times += 1
return times
n=int(input())
lst=tuple(input().split(" "))
print(LRU(lst, 3,n))
【运行测试】
（八）、【Python0006】爬楼梯
【题目描述】
假设一段楼梯共n(n>1)个台阶，小朋友一步最多能上3个台阶，那么小朋友上这段楼梯一共有多少种方法。
【源代码程序】
def climb(num):
if num==1:
return 1
if num==2:
return 2
if num==3:
return 4
else:
sum=climb(num-1)+climb(num-2)+climb(num-3)
return sum
print(climb(int(input())))
【运行测试】
（九）、【Python0007】杨辉三角形
【题目描述】
输出n（0<n）行杨辉三角形，n由用户输入。
【源代码程序】
n = int(input("请输入要打印的杨辉三角的行数: "))
# 初始化杨辉三角的第一行
triangle = [[1]]
# 循环生成杨辉三角
for i in range(1, n):
# 初始化当前行的第一个元素为1
row = [1]
# 循环生成当前行的中间元素
for j in range(1, i):
# 当前元素等于上一行中前一个元素和同一位置元素的和
element = triangle[i - 1][j - 1] + triangle[i - 1][j]
# 将当前元素加入当前行
row.append(element)
# 将当前行的最后一个元素设为1
row.append(1)
# 将当前行加入杨辉三角
triangle.append(row)
# 循环输出杨辉三角
for i in range(n):
# 计算当前行前面需要填充的空格数量
spaces = ' ' * (n - i)
# 用join函数将当前行中的数字转为字符串，并用空格连接
# 然后再在前面添加空格，输出当前行
print(spaces + ' '.join(map(str, triangle[i])))
【运行测试】
（十）、【Python0008】筛法求素数
【题目描述】
用户输入整数n和m（1<n<m<1000），应用筛法求[n,m]范围内的所有素数。
【源代码程序】
def sieve(n, m):
"""
输入两个正整数n和m，返回[n,m]范围内的所有素数的列表
"""
# 初始化一个长度为m-n+1的列表，用于标记数值是否为素数
is_prime = [True] * (m - n + 1)
# 如果n为1，则将1标记为合数
if n == 1:
is_prime[0] = False
# 从2开始，将所有能被2整除的数标记为合数
for i in range(2, int(m ** 0.5) + 1):
for j in range(max(i ** 2, (n + i - 1) // i * i), m + 1, i):
if j >= n and is_prime[j - n]:
is_prime[j - n] = False
# 将所有未被标记为合数的数加入素数列表
primes = [i + n for i in range(m - n + 1) if is_prime[i]]
return primes
# 输入n和m
n, m = map(int, input("请输入n和m(1 < n < m < 1000):").split())
if not 1 < n < m < 1000:
print("输入有误，请重新输入")
n, m = map(int, input("请输入n和m(1 < n < m < 1000):").split())
else:
print("该范围内的所有素数为：", end='')
print(sieve(n, m))
【运行测试】
（十一）、【Python0009】查找鞍点
【题目描述】
对于给定5X5的整数矩阵，设计算法查找出所有的鞍点的信息（包括鞍点的值和行、列坐标，坐标从1开始）。
提示：鞍点的特点：列上最小，行上最大。
【源代码程序】
matrix = []
matrix2 = []
matrix3 = []
for i in range(5):
a = input()
a1 = a.split(" ") # a1中的元素都是字符串，需要转换
for i in a1[::]:
if i == '':
a1.remove(i) # 去掉空元素
a1 = [int(x) for x in a1] # 将其中的元素转为int类型，方便排序
matrix.append(a1) # 插入到一个新列表
for i in range(0, 5):
matrix2 = []
for j in range(0, 5):
matrix2.append(matrix[j][i])
matrix3.append(matrix2) # 将每一列收集起来组合成新的列表
for i in range(0, 5):
for j in range(0, 5):
if matrix[i][j] == max(matrix[i]): # 判断是否为该行最大值
if matrix[i][j] == min(matrix3[j]): # 判断是否为该列最小值
print([i + 1, j + 1, matrix[i][j]], end="")
【运行测试】
（十二）、【Python0010】正整数的因子展开式
【题目描述】
编写程序，输出一个给定正整数x（x>1）的质因子展开式。
【源代码程序】
num = int(input())
newnum = num
text = ""
counter = 2
while counter * counter <= newnum:
if newnum % counter == 0: # 判断是否能够整除2
text = text + str(counter) # 将质因子组合起来
newnum = int(newnum / counter)
else:
counter += 1
if newnum != 1: # 如果结果不为1，就加上目前的newnum质因子
text = text + str(newnum)
if text == "" + str(newnum): # 判断质因子就是其本身
text = str(newnum)
print(str(num) + "=" + text)
【运行测试】
（十三）、【Python0011】牛顿迭代法
【题目描述】
编写程序，使用牛顿迭代法求方程在x附近的一个实根。
【源代码程序】
num = input()
n1 = num.split(" ")
n = []
for i in n1[::]:
if i == '':
n1.remove(i)
for i in n1:
n.append(float(i))
def f(x):
return n[0] * pow(x, 3) + n[1] * pow(x, 2) + n[2] * pow(x, 1) + n[3]
def fd(x):
return 3 * n[0] * pow(x, 2) + 2 * n[1] * pow(x, 1) + n[2]
def newtonMethod(assum):
x = assum
a = f(x)
b = fd(x)
if f(x) == 0.0:
print(round(x, 2))
return x
else:
next = x - a / b
# print('next x = ' + str(next)) # 输出下一条切线的值
if a - f(next) < 1e-6:
print(round(next, 2)) # 设置跳出条件，同时输出满足f(x) = 0 的x的值
else:
return newtonMethod(next) # 递归
newtonMethod(n[4])
