最短路径算法

Dijk1stra算法

图基础知识

• 图
• 图基础操作
• 图的遍历

Dijkstra基础知识

• Dijkstra 算法从指定的节点（源节点）出发，寻找它与图中所有其它节点之间的最短路径。
• Dijkstra 算法会记录当前已知的最短路径，并在寻找到更短的路径时更新。
• 一旦找到源节点与其他节点之间的最短路径，那个节点会被标记为“已访问”并添加到路径中。
• 重复寻找过程，直到图中所有节点都已经添加到路径中。这样，就可以得到从源节点出发访问所有其他节点的最短路径方案。

Dijkstra 只能用在权重为正的图中，因为计算过程中需要将边的权重相加来寻找最短路径。

算法示例

图文详解 Dijkstra 最短路径算法

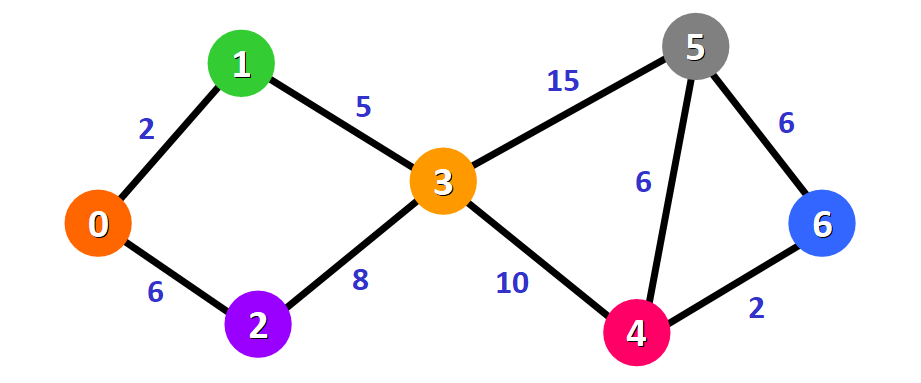
// 邻接矩阵数组：w[a][b] = c 代表从 a 到 b 有权重为 c 的边
// int[][] w = new int[N][N];
// dist[x] = y 代表从「源点/起点」到 x 的最短距离为 y
// int[] dist = new int[N];
// 记录哪些点已经被更新过
// boolean[] vis = new boolean[N];

void dijkstra() {
    // 起始先将所有的点标记为「未更新」和「距离为正无穷」
    Arrays.fill(vis, false);
    Arrays.fill(dist, INF);
    // 只有起点最短距离为 0
    dist[k] = 0;
    // 迭代 n 次
    for (int p = 1; p <= n; p++) {
        // 每次找到「最短距离最小」且「未被更新」的点 t
        int t = -1;
        for (int i = 1; i <= n; i++) {
            if (!vis[i] && (t == -1 || dist[i] < dist[t])) t = i;
        }
        // 标记点 t 为已更新
        vis[t] = true;
        // 用点 t 的「最小距离」更新其他点
        for (int i = 1; i <= n; i++) {
            dist[i] = Math.min(dist[i], dist[t] + w[t][i]);
        }
    }
}

• 时间复杂度：O(n^2)，空间复杂度：O(n^2)

Floyd算法

• 核心思想是，在两个顶点之间插入一个或一个以上的中转点，比较经过与不经过中转点的距离哪个更短

void floyd() {
    // floyd 基本流程为三层循环：
    // 枚举中转点 - 枚举起点 - 枚举终点 - 松弛操作        
    for (int p = 1; p <= n; p++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                w[i][j] = Math.min(w[i][j], w[i][p] + w[p][j]);
            }
        }
    }
}

• 时间复杂度：O(n^3) ，空间复杂度：O(n^2)

Leetcode

743. 网络延迟时间

有 n 个网络节点，标记为 1 到 n

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1

• 1 <= k <= n <= 100
• 1 <= times.length <= 6000
• times[i].length == 3
• 1 <= ui, vi <= n
• ui != vi
• 0 <= wi <= 100
• 所有 (ui, vi) 对都 互不相同（即，不含重复边）

class Solution {
    int N = 110, M = 6010;
    // 邻接矩阵数组：w[a][b] = c 代表从 a 到 b 有权重为 c 的边
    int[][] w = new int[N][N];
    // dist[x] = y 代表从「源点/起点」到 x 的最短距离为 y
    int[] dist = new int[N];
    // 记录哪些点已经被更新过
    boolean[] vis = new boolean[N];
    int INF = 0x3f3f3f3f;
    int n, k;
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; k = _k;
        // 初始化邻接矩阵
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                w[i][j] = w[j][i] = i == j ? 0 : INF;
            }
        }
        // 存图
        for (int[] t : ts) {
            int u = t[0], v = t[1], c = t[2];
            w[u][v] = c;
        }
        // 最短路
        dijkstra();
        // 遍历答案
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            ans = Math.max(ans, dist[i]);
        }
        return ans > INF / 2 ? -1 : ans;
    }
    void dijkstra() {
        // 起始先将所有的点标记为「未更新」和「距离为正无穷」
        Arrays.fill(vis, false);
        Arrays.fill(dist, INF);
        // 只有起点最短距离为 0
        dist[k] = 0;
        // 迭代 n 次
        for (int p = 1; p <= n; p++) {
            // 每次找到「最短距离最小」且「未被更新」的点 t
            int t = -1;
            for (int i = 1; i <= n; i++) {
                if (!vis[i] && (t == -1 || dist[i] < dist[t])) t = i;
            }
            // 标记点 t 为已更新
            vis[t] = true;
            // 用点 t 的「最小距离」更新其他点
            for (int i = 1; i <= n; i++) {
                dist[i] = Math.min(dist[i], dist[t] + w[t][i]);
            }
        }
    }
}

作者：宫水三叶
链接：https://leetcode.cn/problems/network-delay-time/solutions/910056/gong-shui-san-xie-yi-ti-wu-jie-wu-chong-oghpz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。