Statistics : Data Distribution
1、Normal distribution

In probability theory, the normal (or Gaussian or Gauss or Laplace–Gauss) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
The normal distribution is
useful because of the central limit theorem. In its most general form, under
some conditions (which include finite variance), it states that averages of
samples of observations of random variables independently drawn from
independent distributions converge in distribution to the normal, that is, they
become normally distributed when the number of observations is sufficiently
large. Physical quantities that are expected to be the sum of many independent
processes (such as measurement errors) often have distributions that are nearly
normal. Moreover, many results and methods (such as propagation of uncertainty
and least squares parameter fitting) can be derived analytically in explicit
form when the relevant variables are normally distributed.
The normal distribution is
sometimes informally called the bell curve. However, many other distributions
are bell-shaped (such as the Cauchy, Student's t-, and logistic distributions).
link:https://en.wikipedia.org/wiki/Normal_distribution
https://www.mathsisfun.com/data/standard-normal-distribution.html
2、Poisson Distribution
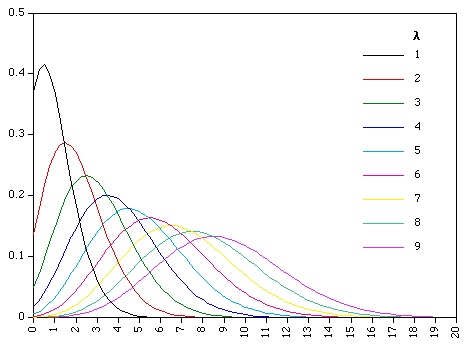
In
probability theory and statistics, the Poisson distribution (French
pronunciation: ; in English often rendered /ˈpwɑːsɒn/), named after French
mathematician Siméon Denis Poisson, is a discrete probability distribution that
expresses the probability of a given number of events occurring in a fixed
interval of time or space if these events occur with a known constant rate and
independently of the time since the last event. The Poisson distribution can
also be used for the number of events in other specified intervals such as
distance, area or volume.
For instance, an
individual keeping track of the amount of mail they receive each day may notice
that they receive an average number of 4 letters per day. If receiving any
particular piece of mail does not affect the arrival times of future pieces of
mail, i.e., if pieces of mail from a wide range of sources arrive independently
of one another, then a reasonable assumption is that the number of pieces of
mail received in a day obeys a Poisson distribution. Other examples that may
follow a Poisson distribution include the number of phone calls received by a
call center per hour and the number of decay events per second from a
radioactive source.
link:https://en.wikipedia.org/wiki/Poisson_distribution
https://www.umass.edu/wsp/resources/poisson/
3、Chi-squared distribution

In
probability theory and statistics, the chi-square distribution (also
chi-squared or χ2-distribution) with k degrees of freedom is the distribution
of a sum of the squares of k independent standard normal random variables. The
chi-square distribution is a special case of the gamma distribution and is one
of the most widely used probability distributions in inferential statistics,
notably in hypothesis testing or in construction of confidence intervals. When
it is being distinguished from the more general noncentral chi-square distribution,
this distribution is sometimes called the central chi-square distribution.
The chi-square
distribution is used in the common chi-square tests for goodness of fit of an
observed distribution to a theoretical one, the independence of two criteria of
classification of qualitative data, and in confidence interval estimation for a
population standard deviation of a normal distribution from a sample standard
deviation. Many other statistical tests also use this distribution, such as
Friedman's analysis of variance by ranks.
link:https://en.wikipedia.org/wiki/Chi-squared_distribution
http://mathworld.wolfram.com/Chi-SquaredDistribution.html
https://www.itl.nist.gov/div898/handbook/eda/section3/eda3666.html
4、Beta distribution
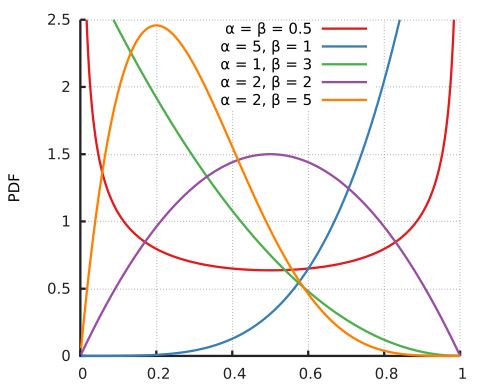
In
probability theory and statistics, the beta distribution is a family of
continuous probability distributions defined on the interval parametrized by two positive shape parameters,
denoted by α and β, that appear as exponents of the random variable and control
the shape of the distribution. It is a special case of the Dirichlet
distribution.
The beta distribution has
been applied to model the behavior of random variables limited to intervals of
finite length in a wide variety of disciplines.
In Bayesian inference, the
beta distribution is the conjugate prior probability distribution for the
Bernoulli, binomial, negative binomial and geometric distributions. For
example, the beta distribution can be used in Bayesian analysis to describe
initial knowledge concerning probability of success such as the probability
that a space vehicle will successfully complete a specified mission. The beta
distribution is a suitable model for the random behavior of percentages and proportions.
The usual formulation of
the beta distribution is also known as the beta distribution of the first kind,
whereas beta distribution of the second kind is an alternative name for the
beta prime distribution.
link:https://en.wikipedia.org/wiki/Beta_distribution



