独树一帜的字符串匹配算法——RK算法
参加了雅虎2015校招，笔试成绩还不错，谁知初面第一题就被问了个字符串匹配，要求不能使用KMP，但要和KMP一样优，当时瞬间就呵呵了。后经过面试官的一再提示，也还是没有成功在面试现场写得。现将该算法记录如下，思想绝对是字符串匹配中独树一帜的
字符串匹配
存在长度为n的字符数组S[0...n-1]，长度为m的字符数组P[0...m-1]，是否存在i，使得SiSi+1...Si+m-1等于P0P1...Pm-1，若存在，则匹配成功，若不存在则匹配失败。
RK算法思想
假设我们有某个hash函数可以将字符串转换为一个整数，则hash结果不同的字符串肯定不同，但hash结果相同的字符串则很有可能相同（存在小概率不同的可能）。
算法每次从S中取长度为m的子串，将其hash结果与P的hash结果进行比较，若相等，则有可能匹配成功，若不相等，则继续从S中选新的子串进行比较。
假设进行下面的匹配：
| S0 | S1 | ... | Si-m+1 | Si-m+2 | ... | Si-1 | Si | Si+1 | ... | Sn-1 |
| P0 | P1 | Pm-2 | Pm-1 |
|
情况一、hash(Si-m+1...Si) == hash(P0...Pm-1)，此时Si-m+1...Si与P0...Pm-1有可能匹配成功。只需要逐字符对比就可以判断是否真的匹配成功，若匹配成功，则返回匹配成功点的下标i-m+1，若不成功，则继续取S的子串Si-m+2...Si+1进行hash
情况二、hash(Si-m+1...Si) != hash(P0...Pm-1)，此时Si-m+1...Si与P0...Pm-1不可能匹配成功，所以继续取S的子串Si-m+2...Si+1进行hash
可以看出，不论情况一还是情况二，都涉及一个共同的步骤，就是继续取S的子串Si-m+2...Si+1进行hash。如果每次都重新求hash结果的话，复杂度为O(m)，整体复杂度为O(mn)。如果可以利用上一个子串的hash结果hash(Si-m+1...Si)，在O(1)的时间内求出hash(Si-m+2...Si+1)，则可以将整体复杂度降低到线性时间
至此，问题的关键转换为如何根据hash(Si-m+1...Si)，在O(1)的时间内求出hash(Si-m+2...Si+1)
设计hash函数为：hash(Si-m+1...Si) = Si-m+1*xm-1 + Si-m+2*xm-2 + ... + Si-1*x + Si
则 hash(Si-m+2...Si+1) = Si-m+2*xm-1 + Si-m+3*xm-2 + ... + Si*x + Si+1
= (hash(Si-m+1...Si) - Si-m+1*xm-1) * x + Si+1
hash结果过大怎么办？对某个大素数取余数即可（经典方法），称其为HASHSIZE
所以，hash函数更新为：hash(Si-m+1...Si) = (Si-m+1*xm-1 + Si-m+2*xm-2 + ... + Si-1*x + Si) % HASHSIZE
则 hash(Si-m+2...Si+1) = (Si-m+2*xm-1 + Si-m+3*xm-2 + ... + Si*x + Si+1) % HASHSIZE
= ((hash(Si-m+1...Si) - Si-m+1*xm-1) * x + Si+1) % HASHSIZE
设计算法时需要注意的几点：
1、可提前计算出hash(P0...Pm-1)和xm-1并保存
2、char c 的取值范围为0~255，计算hash结果时会自动类型提升为int，为避免符号位扩展，使用 (unsigned int)c & 0x000000FF
3、hash(Si-m+1...Si) - Si-m+1*xm-1 的结果可能为负数，需先加上 Si-m+1*HASHSIZE 并最后 % HASHSIZE 来保证结果非负
具体代码如下：
1 #define UNSIGNED(x) ((unsigned int)x & 0x000000FF) 2 #define HASHSIZE 10000019 3 4 int hashMatch(char* s, char* p) { 5 int n = strlen(s); 6 int m = strlen(p); 7 if (m > n || m == 0 || n == 0) 8 return -1; 9 // sv为S子串的hash结果，pv为字符串p的hash结果，base为x的m-1次方 10 unsigned int sv = UNSIGNED(s[0]), pv = UNSIGNED(p[0]), base = 1; 11 int i, j; 12 // 初始化 sv, pv, base 13 for (i = 1; i < m; i++) { 14 pv = (pv * 10 + UNSIGNED(p[i])) % HASHSIZE; 15 sv = (sv * 10 + UNSIGNED(s[i])) % HASHSIZE; 16 base = (base * 10) % HASHSIZE; 17 } 18 i = m - 1; 19 do { 20 // 情况一、hash结果相等 21 if (sv == pv) { 22 for (j = 0; j < m && s[i - m + 1 + j] == p[j]; j++) 23 ; 24 if (j == m) 25 return i - m + 1; 26 } 27 i++; 28 if (i >= n) 29 break; 30 // O(1)时间更新S子串的hash结果 31 sv = (sv + UNSIGNED(s[i - m]) * (HASHSIZE - base)) % HASHSIZE; 32 sv = (sv * 10 + UNSIGNED(s[i])) % HASHSIZE; 33 } while (i < n); 34 35 return -1; 36 }
时间复杂度分析：循环复杂度O(n)，hash结果相等时的逐字符匹配复杂度为O(m)，整体时间复杂度为O(m+n)。空间复杂度为O(1)
运行时间PK
随机生成10亿字节（1024*1024*1023）的字符串保存到文件num.txt中，读出到字符串S中，P长度为1024*10字节，分别使用RK算法和KMP算法进行实验
从文件num.txt中读取字符串到S中所需时间为：
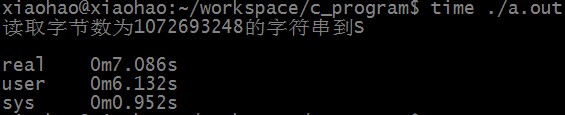
匹配成功时，RK算法匹配所需时间为：
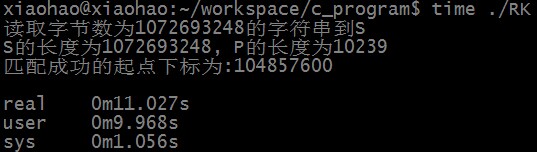
匹配成功时，KMP算法匹配所需时间为：
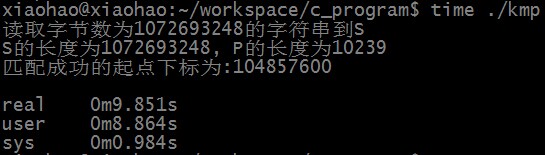
匹配不成功时，RK算法匹配所需时间为：
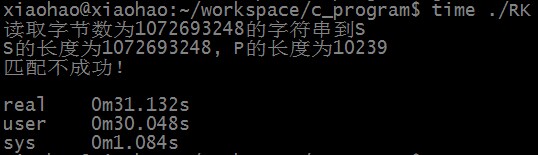
匹配不成功时，KMP算法匹配所需时间为：
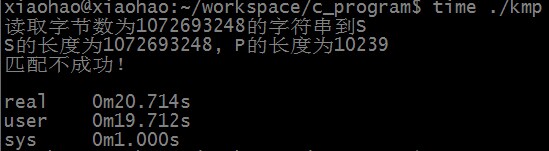
可以看出，RK算法和KMP算法均可以在线性时间内完成匹配，RK算法时间稍慢的原因主要有两点，一是数学取模运算，二是hash结果相同不一定完全匹配，需要再逐字符进行对比。统计hash结果相等但字符串不一定匹配的情况发现，匹配不成功时有105次hash结果相等但字符串不匹配的情况。S中长度为10239的子串个数大约为10亿，所以hash结果相等但不匹配的概率大约为一千万分之一（刚好约等于1/HASHSIZE），所以时间复杂度精确值应为O(n) + O(m*n/HASHSIZE)。
算法优化
在上面的测试中RK算法还是慢于KMP的，优化从两点出发：一是用其他运算代替取模运算，二是降低hash冲突。
先解决降低冲突的问题，在之前的代码中，我们使用了x=10，假设存在char值为2,20,200的三个字符a,b,c，可以发现a*1000，b*100，c*10的hash结果是相同的，也就是发生了冲突，所以取大于等于256的数做x则可以避免这种冲突。另外HASHSIZE的大小也会决定冲突发生的概率，HASHSIZE最大可以多大呢？对于unsigned int来说，总共有2^32次方个，所以可以取HASHSIZE为2^32次方。而计算机对于大于等于2^32次方的数会自动舍弃高位，其刚好等价于对2^32次方取模，即对HASHSIZE取模，所以便可以从代码中去掉取模运算。
优化后的代码如下（代码中d即上文中的x）：
1 #define UNSIGNED(x) ((unsigned char)x) 2 #define d 257 3 4 int hashMatch(char* s, char* p) { 5 int n = strlen(s); 6 int m = strlen(p); 7 if (m > n || m == 0 || n == 0) 8 return -1; 9 // sv为s子串的hash结果，pv为p的hash结果，base为d的m-1次方 10 unsigned int sv = UNSIGNED(s[0]), pv = UNSIGNED(p[0]), base = 1; 11 int i, j; 12 int count = 0; 13 // 初始化sv, pv, base 14 for (i = 1; i < m; i++) { 15 pv = pv * d + UNSIGNED(p[i]); 16 sv = sv * d + UNSIGNED(s[i]); 17 base = base * d; 18 } 19 i = m - 1; 20 do { 21 // 情况一，hash结果相等 22 if (!(sv ^ pv)) { 23 for (j = 0; j < m && s[i - m + 1 + j] == p[j]; j++) 24 ; 25 if (j == m) 26 return i - m + 1; 27 } 28 i++; 29 if (i >= n) 30 break; 31 // O(1)时间内更新sv, sv + UNSIGNED(s[i - m]) * (~base + 1)等价于sv - UNSIGNED(s[i - m]) * base 32 sv = (sv + UNSIGNED(s[i - m]) * (~base + 1)) * d + UNSIGNED(s[i]); 33 } while (i < n); 34 35 return -1; 36 }
匹配成功时，优化后RK算法匹配所需时间为：
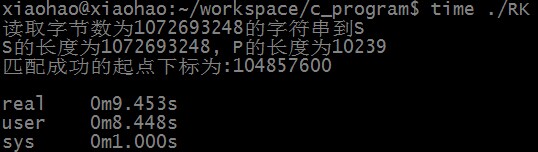
匹配不成功时，优化后RK算法匹配所需时间为：
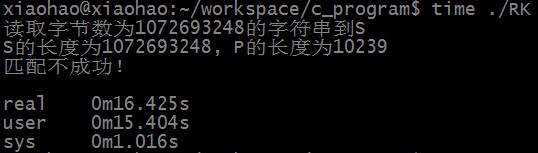
可以看出，优化后的RK算法已经在时间上优于KMP了。而且大小为2^32次方的HASHSIZE也保证了S的10亿个子串基本不会发生冲突。
