矩阵计数

ps:花了很久才看懂别人的暴力写法。不考虑有黑点的矩形,以 ( i,j )为右下角高度为1, 2,3, ······,i 的矩形分别都有 j 个。

当有黑点时,就要考虑枚举的高度是否是合法,比如说高度为2的矩形,但高度为1的矩形中有黑点,那么高度为2的矩形就一定不会是 j 个。
const int N = 100005; int n, m, k, cas, up[105]; bool sp[N][105]; int main() { cas = 1; BEGIN() { mem(sp, 0); mem(up, 0); sc(n), sc(m), sc(k); Rep(i, 1, k) { int a, b; sc(a), sc(b); sp[a][b] = 1; } LL ans = 0; Rep(i, 1, n) { Rep(j, 1, m) if (sp[i][j]) up[j] = i; Rep(j, 1, m) { int h = 0; for (int k = j; k; --k) { h = max(h, up[k]); ans += (i - h); } } } printf("Case #%d: %lld\n", cas++, ans); } return 0; }
ps:单调栈优化并维护前缀和(既存在递推关系)
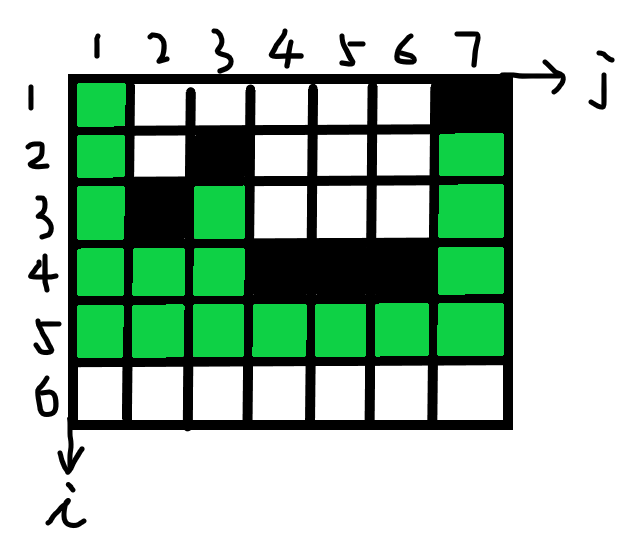
枚举到第 5 行,维护一个单调非严格递增的栈,假设已经算出了以(5,j)为右下角的矩形个数,怎么求(5,j + 1)为右下角的矩形个数呢?设 j + 1 列的高度(从当前位置开始向上走直到遇到第一个黑色位置或者边界的距离)为h,如果 h >= S.top(),那么新增的矩形个数就是d,既sum(j + 1) = sum(j) + d;如果 h < S.top(),那么新增的个数是在栈中比h大的元素个数乘以h。因为以h为高的矩形是可以向左扩展的。
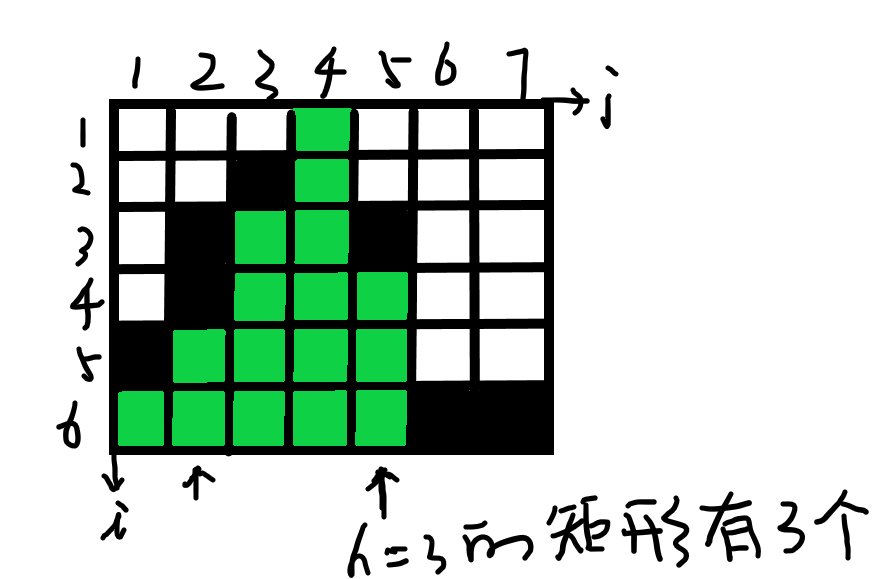
看图:sum( j = 5 ) = sum( j = 2) + 3 * h.(以(6,5)为右下角高度为h的矩形有三个)
注意:①搞清楚递推关系。②弹出多少个数就要压入多少个数。
const int N = 100005; int n, m, k, cas, up[105], S[105]; bool sp[N][105]; int main() { cas = 1; BEGIN() { mem(sp, 0); mem(up, 0); sc(n), sc(m), sc(k); Rep(i, 1, k) { int a, b; sc(a), sc(b); sp[a][b] = 1; } LL ans = 0; Rep(i, 1, n) { LL sum = 0; int top = 0; Rep(j, 1, m) { if (sp[i][j]) up[j] = i; int d = i - up[j]; if (!d) { top = 0; sum = 0; } else { int cnt = 1; while(top && S[top - 1] > d) { sum -= S[top - 1]; // 因为是维护的前缀和,S.top() > d 的位置的贡献是无用的,得减去。这里不太好理解 top --; cnt ++; } Rep(k, 1, cnt) { sum += d; S[top++] = d; // 弹出多少个数就压入多少个数(一切都是为了前缀和) } } ans += sum; /* 错误得写法,没有正确得维护前缀和 if (sp[i][j]) { up[j] = i; top = 0; sum = 0; } int d = i - up[j]; int cnt = 1; while(top && S[top - 1] >= d) { sum -= S[top - 1]; top--; cnt++; } S[top++] = d; Rep(j, 1, cnt) sum += d; ans += sum; */ } } printf("Case #%d: %lld\n", cas++, ans); } return 0; }
数据范围:1 <= n <= 1e9,1 <= m <= 1e9,1 <= k <= 5000
ps:显然不能用上面的方法。 k 只有5000个,所以:
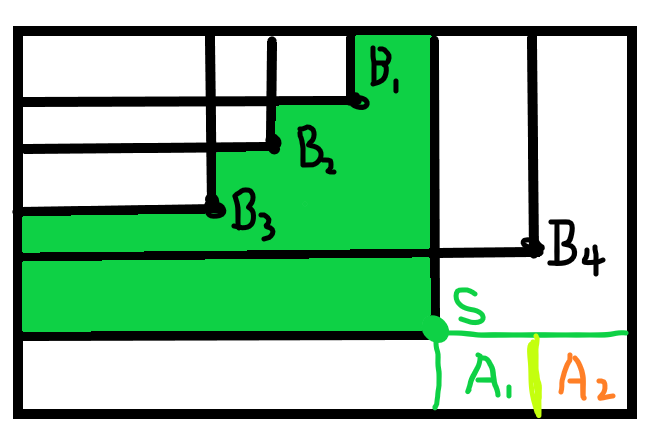
点S(x,y),以(1,1)为左上角,(x,y)为右下角的矩形叫SP,和以 (x,y)为左上角,(n,m)为右下角的矩形叫SQ,假设 点P∈SP,点Q∈SQ,那么以P点为左上角,Q点为右下角形成的矩形一定包括点S。讨论矩形SP,并计算包含第 i 个点(点S)的矩形个数:记 F ( 矩形X)= cnt(矩形X包含点的个数),首先点集{1 ~ ( i - 1)}可以分为两部分,一部分点在SP内,另一部分不在SP内:{B1,B2,B3},{B4}。仔细观察SQ矩形内的点在SP内那部分的点会产生贡献,
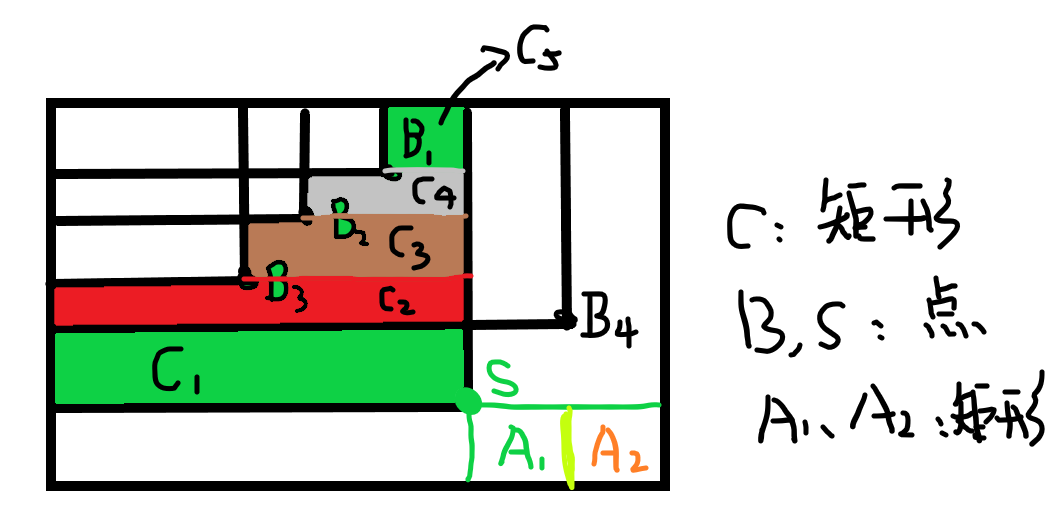
那么包含点S的矩形个数 ans = F( A1 + A2 ) * F( C1) + F( A1 ) * F( C2 ) + F( A1 ) * F( C3 ) + F( A1 ) * F( C4 ) + F( A1 ) * F( C5 )。既SQ内的点(作为矩形的右下角)只会和有颜色那部分的点(作为矩形的左上角)形成的矩形才是去重后包含S点矩形的个数。且不在SP内的点集{B4}会限制SQ矩形的宽度(矩形A2内的点的贡献在点B4就已经计算过)。
const int mod = 1000000007; P p[5005]; int n, m, C; bool cmp(P x, P y) { if (x.first == y.first) return x.second < y.second; return x.first < y.first; } int main() { sc(n), sc(m), sc(C); Rep(i, 1, C) sc(p[i].first), sc(p[i].second); sort(p + 1, p + C + 1, cmp); LL ans = 0; Rep(i, 1, C) { int l = 0, r = m + 1; for (int j = i - 1; ~j; --j) { ans += 1ll * (p[i].second - l) * (r - p[i].second) % mod * 1ll * (p[j + 1].first - p[j].first) % mod * (n - p[i].first + 1) % mod; ans %= mod; if (p[j].second > p[i].second) r = min(r, p[j].second); if (p[j].second < p[i].second) l = max(l, p[j].second); } } LL res = ((1ll * n * (n + 1) / 2) % mod) * ((1ll * (m + 1) * m / 2) % mod) % mod; cout << (res - ans + mod) % mod << endl; return 0; }
如果看懂了dp的做法,就能去做 51Nod 1291了。orzzzzz!


