Kth number -hdu2665

归并树，划分树，主席树都能做。

https://www.bilibili.com/video/av4619406/?p=2 资源，对主席树的理解还差了一点，不是很明白它是怎么更新每个节点左儿子和右儿子编号的。

主席树：函数式线段树，步骤：① hash ② 建树 ③ 询问；

（1）

建议学主席树的朋友看完我浅陋的总结后，移步到我提供的资源，里面的up主语言规范一点。它是多颗线段树何合在一起的。多颗线段树？对区间 [ 1 , i ]（ i 取 1 ， 2 ， 3  ， 4 ，··· ， n ）都建立线段树，所以有n颗。对于这n颗线段树要明白两个问题！！！① 它们都是一个模样。② 线段树的节点都涵盖了哪些元素：区间编号、这个区间包含了多少个数。然后下一步再思考它们是怎么合的？

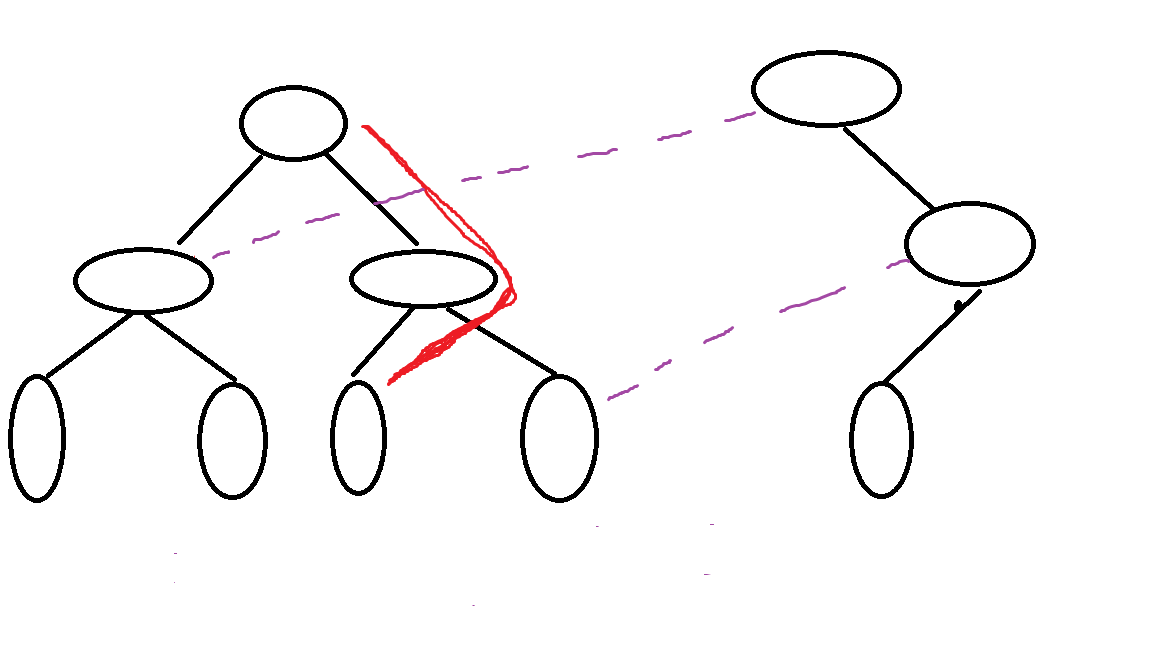
加进去一个数只会影响一条链，所以为了避免空间的浪费，需要把新的节点连上没有变化的儿子节点，如图中紫色的线，这一点体现在代码中就是 T [ ++cnt ] = T [ pre ]，新的节点复制了原来的节点，同时继承了原节点的儿子编号，而这个节点要修改左儿子的编号或者右儿子的编号怎么办？引用，如果不明白就从1开始模拟两三个数的更新过程就明白了。-------------------如有错误请指正，感谢！还有一个问题没说，这n颗线段树满足加减性质的，因为每颗线段树相当于一个前缀和。详细证明我也不会，^_^！！！！

（2）

https://blog.finaltheory.me/algorithm/Chairman-Tree.html#content-heading  资源二  主席树的结构弄清楚后，该理解前缀和的意义了，不仅从字面上，还要理解它在结构上是怎么体现的。root [ r ] - root [ l - 1 ]得到的是相当于只插入了原序列中[l, r]元素的一颗记录了区间数字个数的线段树。

#pragma warning(disable:4996)
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long 
#define mem(arr,in) memset(arr,in,sizeof(arr))
using namespace std;

const int maxn = 1e5 + 5;

int n, m, cnt, kase;
int root[maxn], a[maxn];

struct node { int l, r, sum; } T[maxn * 20];

vector<int> v;
int getid(int x) { return lower_bound(v.begin(), v.end(), x) - v.begin() + 1; }
    
void Update(int l, int r, int &rt, int pre, int pos) {
    T[++cnt] = T[pre], T[cnt].sum++, rt = cnt;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (mid >= pos) Update(l, mid, T[rt].l, T[pre].l, pos);
    else Update(mid + 1, r, T[rt].r, T[pre].r, pos);
}

int Query(int l, int r, int x, int y, int k) {
    if (l == r) return l;
    int mid = (l + r) >> 1;
    int sum = T[T[y].l].sum - T[T[x].l].sum;
    if (sum >= k) return Query(l, mid, T[x].l, T[y].l, k);
    else return Query(mid + 1, r, T[x].r, T[y].r, k - sum);
}

int main()
{    
    scanf("%d", &kase);
    while (kase--) {
        v.clear(); cnt = 0;

        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++) scanf("%d", &a[i]), v.push_back(a[i]);

        sort(v.begin(), v.end());
        v.erase(unique(v.begin(), v.end()), v.end());

        for (int i = 1; i <= n; i++) Update(1, n, root[i], root[i - 1], getid(a[i]));
        for (int i = 1; i <= m; i++) {
            int x, y, k;
            scanf("%d%d%d", &x, &y, &k);
            printf("%d\n", v[Query(1, n, root[x - 1], root[y], k) - 1]);
        }
    }
    return 0;
}