Educational Codeforces Round 40 (Rated for Div. 2)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A. Diagonal Walking

Mikhail walks on a 2D plane. He can go either up or right. You are given a sequence of Mikhail's moves. He thinks that this sequence is too long and he wants to make it as short as possible.

In the given sequence moving up is described by character U and moving right is described by character R. Mikhail can replace any pair of consecutive moves RU or UR with a diagonal move (described as character D). After that, he can go on and do some other replacements, until there is no pair of consecutive moves RU or UR left.

Your problem is to print the minimum possible length of the sequence of moves after the replacements.

Input

The first line of the input contains one integer n (1 ≤ n ≤ 100) — the length of the sequence. The second line contains the sequence consisting of n characters U and R.

Output

Print the minimum possible length of the sequence of moves after all replacements are done.

Examples

Input

Copy

5
RUURU

Output

3

Input

Copy

17
UUURRRRRUUURURUUU

Output

13

Note

In the first test the shortened sequence of moves may be DUD (its length is 3).

In the second test the shortened sequence of moves can be UUDRRRDUDDUUU (its length is 13).

题解：以R为点优先消去左边的U。

#pragma warning(disable:4996)
#include<map>
#include<queue>
#include<string>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int INF = 1e9 + 7;
const int maxn = 1005;

int main()
{
    int n;
    string s;
    while (cin >> n >> s) {
        int t = 0;
        bool use[105];
        memset(use, 0, sizeof(use));
        for (int i = 0; i < n; i++) {
            if (s[i] == 'R') {
                if (i == 0) {
                    if (s[i + 1] == 'U') { use[i + 1] = 1; t++; }
                    continue;
                }
                if (s[i - 1] == 'U' && !use[i - 1]) { use[i - 1] = 1; t++; }
                else if (s[i + 1] == 'U' && !use[i + 1]) { use[i + 1] = 1; t++; }
            }
        }
        cout << n - t << endl;
    }
    return 0;
}

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B. String Typing

You are given a string s consisting of n lowercase Latin letters. You have to type this string using your keyboard.

Initially, you have an empty string. Until you type the whole string, you may perform the following operation:

• add a character to the end of the string.

Besides, at most once you may perform one additional operation: copy the string and append it to itself.

For example, if you have to type string abcabca, you can type it in 7 operations if you type all the characters one by one. However, you can type it in 5 operations if you type the string abc first and then copy it and type the last character.

If you have to type string aaaaaaaaa, the best option is to type 4 characters one by one, then copy the string, and then type the remaining character.

Print the minimum number of operations you need to type the given string.

Input

The first line of the input containing only one integer number n (1 ≤ n ≤ 100) — the length of the string you have to type. The second line containing the string s consisting of n lowercase Latin letters.

Output

Print one integer number — the minimum number of operations you need to type the given string.

Examples

Input

Copy

7
abcabca

Output

5

Input

Copy

8
abcdefgh

Output

8

Note

The first test described in the problem statement.

In the second test you can only type all the characters one by one

题解：读懂题意，copy操作只能用一次，且是复制前面的所有字符。脑部了n重题意，花了一个多小时。

#pragma warning(disable:4996)
#include<map>
#include<queue>
#include<string>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int INF = 1e9 + 7;
const int maxn = 1005;

string s;
int n;

int Find(int x) {
    string a;
    for (int i = 0; i < x; i++) a += s[i];


    bool flag = true;
    int t = 0;
    for (int i = x; i < n; i++) {
        if (s[i] != a[t++]) flag = false;
        if (t == a.size() || !flag) break;
    }

    if (t != a.size() || !flag) return 0;
    else return x;
}

int main()
{
    while (cin >> n >> s) {
        int ans = 0;
        for (int i = 1; i < n; i++) ans = max(ans, Find(i));
        if (!ans) cout << n << endl;
        else cout << n - ans + 1 << endl;
    }
    return 0;
}

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　C. Matrix Walk

There is a matrix A of size x × y filled with integers. For every 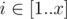, 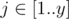A_i, j = y(i - 1) + j. Obviously, every integer from [1..xy] occurs exactly once in this matrix.

You have traversed some path in this matrix. Your path can be described as a sequence of visited cells a₁, a₂, ..., a_n denoting that you started in the cell containing the number a₁, then moved to the cell with the number a₂, and so on.

From the cell located in i-th line and j-th column (we denote this cell as (i, j)) you can move into one of the following cells:

1. (i + 1, j) — only if i < x;
2. (i, j + 1) — only if j < y;
3. (i - 1, j) — only if i > 1;
4. (i, j - 1) — only if j > 1.

Notice that making a move requires you to go to an adjacent cell. It is not allowed to stay in the same cell. You don't know x and y exactly, but you have to find any possible values for these numbers such that you could start in the cell containing the integer a₁, then move to the cell containing a₂ (in one step), then move to the cell containing a₃ (also in one step) and so on. Can you choose x and y so that they don't contradict with your sequence of moves?

Input

The first line contains one integer number n (1 ≤ n ≤ 200000) — the number of cells you visited on your path (if some cell is visited twice, then it's listed twice).

The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹) — the integers in the cells on your path.

Output

If all possible values of x and y such that 1 ≤ x, y ≤ 10⁹ contradict with the information about your path, print NO.

Otherwise, print YES in the first line, and in the second line print the values x and y such that your path was possible with such number of lines and columns in the matrix. Remember that they must be positive integers not exceeding 10⁹.

Examples

Input

Copy

8
1 2 3 6 9 8 5 2

Output

Note

The matrix and the path on it in the first test looks like this:

3 3

Input

Copy

6
1 2 1 2 5 3

Output

NO

题解：注意几种特殊情况。（1）存在原地踏步（2）因为每步只能移向相邻的格子，所以相邻差（i 与 i+1)只能是1和y（3）判断越界

#pragma warning(disable:4996)
#include<map>
#include<queue>
#include<string>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int INF = 1e4 + 7;
const int maxn = 200005;

int n;
int a[maxn];

int main()
{
    while (cin >> n) {
        int y = -1, mam = 0;
        for (int i = 1; i <= n; i++) {
            cin >> a[i]; mam = max(mam, a[i]);
        }
        /*判断否只在一行上移动*/
        bool flag = true;
        for (int i = 2; i <= n; i++) {
            int k = abs(a[i] - a[i - 1]);
            if (k == 1) continue;
            if (k == 0) { flag = false; break; }
            y = k;
        }
        if (flag && y == -1) { printf("YES\n%d %d\n", maxn, mam); continue; }
        /*判断是否有多个y值*/
        for (int i = 2; i <= n; i++) {
            int k = abs(a[i] - a[i - 1]);
            if (k != 1 && k != y) { flag = false; break; }
        }
        /*判断越界*/
        for (int i = 1; i < n; i++) {
            if (a[i] % y == 1) {
                if (a[i + 1] - a[i] != 1 && a[i + 1] - a[i] != y && a[i] - a[i + 1] != y) {
                    flag = false;
                    break;
                }
            }
            if (a[i] % y == 0) {
                if (a[i] - a[i + 1] != 1 && a[i + 1] - a[i] != y && a[i] - a[i + 1] != y) {
                    flag = false;
                    break;
                }
            }
        }
        
        if (!flag) printf("NO\n");
        else printf("YES\n%d %d\n", mam, y);
    }
    return 0;
}

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D. Fight Against Traffic

Little town Nsk consists of n junctions connected by m bidirectional roads. Each road connects two distinct junctions and no two roads connect the same pair of junctions. It is possible to get from any junction to any other junction by these roads. The distance between two junctions is equal to the minimum possible number of roads on a path between them.

In order to improve the transportation system, the city council asks mayor to build one new road. The problem is that the mayor has just bought a wonderful new car and he really enjoys a ride from his home, located near junction s to work located near junction t. Thus, he wants to build a new road in such a way that the distance between these two junctions won't decrease.

You are assigned a task to compute the number of pairs of junctions that are not connected by the road, such that if the new road between these two junctions is built the distance between s and t won't decrease.

Input

The firt line of the input contains integers n, m, s and t (2 ≤ n ≤ 1000, 1 ≤ m ≤ 1000, 1 ≤ s, t ≤ n, s ≠ t) — the number of junctions and the number of roads in Nsk, as well as the indices of junctions where mayors home and work are located respectively. The i-th of the following m lines contains two integers u_i and v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i), meaning that this road connects junctions u_i and v_i directly. It is guaranteed that there is a path between any two junctions and no two roads connect the same pair of junctions.

Output

Print one integer — the number of pairs of junctions not connected by a direct road, such that building a road between these two junctions won't decrease the distance between junctions s and t.

Examples

Input

Copy

5 4 1 5
1 2
2 3
3 4
4 5

Output

0

Input

Copy

5 4 3 5
1 2
2 3
3 4
4 5

Output

5

Input

Copy

5 6 1 5
1 2
1 3
1 4
4 5
3 5
2 5

题解：枚举所有可能加的边。然后判断过这条边的最短路是不是比s-t的最短路长就行了。

感受：fuckkkkkkk。那条边可以顺着走也可以逆着走，比如说( i , j )，可以是 i 到 j，也可以是 j 到 i。wa了4次。。。

#pragma warning(disable:4996)
#include<map>
#include<queue>
#include<string>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int INF = 1e9 + 7;
const int maxm = 1005;

struct node {
    int to, next, va;
}e[4*maxm];

int n, m, s, t, tot;
int head[maxm], d[maxm], use[maxm], mmp[maxm][maxm];

void Inite() {
    tot = 0;
    memset(mmp, 0, sizeof(mmp));
    memset(head, -1, sizeof(head));
}

void addedge(int u, int v) {
    e[tot].to = v;
    e[tot].va = 1;
    e[tot].next = head[u];
    head[u] = tot++;
}

void DJS(int sta) {
    memset(use, 0, sizeof(use));
    for (int i = 1; i <= n; i++) d[i] = INF;

    d[sta] = 0;
    while (true) {
        int v = -1;
        for (int i = 1; i <= n; i++) if (!use[i] && (v == -1 || d[i] < d[v])) v = i;
        if (v == -1) break;
        use[v] = 1;
        for (int i = head[v]; i != -1; i = e[i].next) {
            int u = e[i].to;
            d[u] = min(d[u], d[v] + e[i].va);
        }
    }
}

int main()
{
    while (scanf("%d%d%d%d", &n, &m, &s, &t) != EOF) {
        Inite();
        for (int i = 1; i <= m; i++) {
            int u, v;
            scanf("%d%d", &u, &v);
            addedge(u, v);
            addedge(v, u);
            mmp[u][v] = 1;
            mmp[v][u] = 1;
        }
        int a[maxm], b[maxm];

        DJS(s);
        for (int i = 1; i <= n; i++) a[i] = d[i];
    
        DJS(t);
        for (int i = 1; i <= n; i++) b[i] = d[i];
    

        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = i + 1; j <= n; j++) {
                if (!mmp[i][j] && a[i] + 1 + b[j] >= a[t] && a[j] + 1 + b[i] >= a[t]) cnt++;
            }
        }
        printf("%d\n", cnt);
    }
    return 0;
}

 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　E. Water Taps

Consider a system of n water taps all pouring water into the same container. The i-th water tap can be set to deliver any amount of water from 0 to a_i ml per second (this amount may be a real number). The water delivered by i-th tap has temperature t_i.

If for every 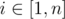you set i-th tap to deliver exactly x_i ml of water per second, then the resulting temperature of water will be 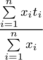(if 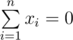, then to avoid division by zero we state that the resulting water temperature is 0).

You have to set all the water taps in such a way that the resulting temperature is exactly T. What is the maximum amount of water you may get per second if its temperature has to be T?

Input

The first line contains two integers n and T (1 ≤ n ≤ 200000, 1 ≤ T ≤ 10⁶) — the number of water taps and the desired temperature of water, respectively.

The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁶) where a_i is the maximum amount of water i-th tap can deliver per second.

The third line contains n integers t₁, t₂, ..., t_n (1 ≤ t_i ≤ 10⁶) — the temperature of water each tap delivers.

Output

Print the maximum possible amount of water with temperature exactly T you can get per second (if it is impossible to obtain water with such temperature, then the answer is considered to be 0).

Your answer is considered correct if its absolute or relative error doesn't exceed 10^- 6.

题解：竟然是贪心。对式子化简得：

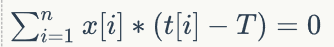
记所有正项的和为sum1，所有负项的和为sum2（代入的是 a[i]）。sum1+sum2=0;如果sum1>sum2，说明负的可以全部加上，然后排序。sum1<sum2同理。

感受：少乘了个1LL，wa到怀疑人生，贪心体现在相同的项，t[i]越小x[i]越大，所以会用上排序。

#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int maxn = 2e5 + 5;

struct node { int a, t; } p[maxn], q[maxn];

bool cmp1(node a, node b) { return a.t < b.t; }
bool cmp2(node a, node b) { return a.t > b.t; }

int n, T;
int a[maxn], t[maxn];

int main()
{
    while (scanf("%d%d", &n, &T) != EOF) {

        int cnt1 = 0, cnt2 = 0;
        double sum1 = 0, sum2 = 0;
        ll tot1 = 0, tot2 = 0;
        double ans = 0;
    
        for (int i = 1; i <= n; i++) scanf("%d", a + i);
        for (int i = 1; i <= n; i++) scanf("%d", t + i);

        for (int i = 1; i <= n; i++) {
            if (t[i] >= T) {
                tot1 += a[i];
                sum1 += 1LL*(t[i] - T)*a[i];
                p[cnt1].a = a[i];
                p[cnt1].t = t[i];
                cnt1++;
            }
            else {
                tot2 += a[i];
                sum2 += 1LL*(T - t[i])*a[i];
                q[cnt2].a = a[i];
                q[cnt2].t = t[i];
                cnt2++;
            }
        }

        sort(p, p + cnt1, cmp1);
        sort(q, q + cnt2, cmp2);

        if (sum1 >= sum2) {
            ans = tot2;
            double temp = 0;
            for (int i = 0; i < cnt1; i++) {
                double k = 1.0*p[i].a*(p[i].t - T);
                if (temp + k <= sum2) {
                    temp += k;
                    ans += p[i].a;
                }
                else {
                    ans += (sum2 - temp) / (p[i].t - T);
                    break;
                }
            }
            printf("%.8lf\n", ans);
        }
        else {
            ans = tot1;
            double temp = 0;
            for (int i = 0; i < cnt2; i++) {
                double k = 1.0*q[i].a*(T - q[i].t);
                if (temp + k <= sum1) {
                    temp += k;
                    ans += q[i].a;
                }
                else {
                    ans += (sum1 - temp) / (T - q[i].t);
                    break;
                }
            }
            printf("%.8lf\n", ans);
        }

    }
    return 0;
}

 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　F. Runner's Problem

You are running through a rectangular field. This field can be represented as a matrix with 3 rows and m columns. (i, j) denotes a cell belonging to i-th row and j-th column.

You start in (2, 1) and have to end your path in (2, m). From the cell (i, j) you may advance to:

• (i - 1, j + 1) — only if i > 1,
• (i, j + 1), or
• (i + 1, j + 1) — only if i < 3.

However, there are n obstacles blocking your path. k-th obstacle is denoted by three integers a_k, l_k and r_k, and it forbids entering any cell (a_k, j) such that l_k ≤ j ≤ r_k.

You have to calculate the number of different paths from (2, 1) to (2, m), and print it modulo 10⁹ + 7.

感受：c++没学好啊。。。看大神的代码都很费力，还好明白了坐标离散和矩阵的快速幂，总算学到了一些知识和技巧。照着网上巨佬的代码手抄了一份。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

template <class T>
struct matrix {
    vector< vector<T> > a;
    int n, m;
    matrix(int n = 1, int m = 1) :n(n), m(m) {
        assert(n > 0 && m > 0);
        a = vector< vector<T> >(n);
        for (int i = 0; i < n; i++) a[i] = vector<T>(m);
    }
    matrix& operator << (const string& s) {
        stringstream ss(s);
        T x;
        for (int i = 0; i < n*m && ss >> x; i++) a[i / m][i%m] = x;
    }
    T& operator()(int x, int y) { return a[x][y]; }
    matrix modmul(matrix &b, T mod)const {
        assert(m == b.n);
        matrix<T> res(n, b.m);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < b.m; j++) {
                for (int k = 0; k < m; k++) {
                    T tmp = a[i][k] * b.a[k][j] % mod;
                    res.a[i][j] = (res.a[i][j] + tmp) % mod;
                }
            }
        }
        return res;
    }
    matrix modpow(T e, T mod)const {
        assert(n == m);
        matrix<T> a = *this, res(n, n);
        for (int i = 0; i < n; i++) res.a[i][i] = 1;
        for (; e > 0; e >>= 1) {
            if (e & 1) res = res.modmul(a, mod);
            a = a.modmul(a, mod);
        }
        return res;
    }
    inline void set(int r, int c, string s, T x = 0) {
        assert(!(r < 0 && c < 0) && !(r >= 0 && c >= 0));
        stringstream ss(s);
        for (int i = 0; ((c < 0 && i < m) || (c >= 0 && i < n)) && ss >> x; i++) c < 0 ? a[r][i] = x : a[i][c] = x;
    }
};

const int maxn = 1e4 + 4;
const int mod = 1e9 + 7;

typedef matrix<ll> mat;

map<ll, int> mp;

int n, nn;
int a[maxn], s[4][4 * maxn];
ll m, b[4*maxn], l[maxn], r[maxn];

int main()
{    
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i] >> l[i] >> r[i];
        b[i] = l[i] - 1;
        b[n + i] = l[i];
        b[2 * n + i] = r[i];
        b[3 * n + i] = r[i] + 1;
    }

    b[4 * n + 1] = 1;
    b[4 * n + 2] = m;

    sort(b + 1, b + 4 * n + 3);
    nn = unique(b + 1, b + 4 * n + 3) - b - 1;

    for (int i = 1; i <= nn; i++) mp[b[i]] = i;
    for (int i = 1; i <= n; i++) {
        int id = a[i];
        int lb = mp[l[i]];
        int rb = mp[r[i]];
        s[id][lb]++;
        s[id][rb + 1]--;
    }
    for (int i = 1; i <= 3; i++) {
        for (int j = 1; j <= nn; j++) s[i][j] += s[i][j - 1];
    }

    mat A(3, 3), ans(3, 1);
    A << "1 1 0 1 1 1 0 1 1";
    ans << "0 1 0";
    for (int i = 2; i <= nn; i++) {
        mat B = A;
        for (int j = 1; j <= 3; j++) {
            if (s[j][i] > 0) B.set(j - 1, -1, "0 0 0");
            if (s[j][i - 1] > 0) B.set(-1, j - 1, "0 0 0");
        }
        ans = B.modpow(b[i] - b[i - 1], mod).modmul(ans, mod);
    }
    cout << ans(1, 0) << endl;

    return 0;
}