Fast Bit Calculations LightOJ - 1032

A bit is a binary digit, taking a logical value of either 1 or 0 (also referred to as "true" or "false" respectively). And every decimal number has a binary representation which is actually a series of bits. If a bit of a number is 1 and its next bit is also 1 then we can say that the number has a 1 adjacent bit. And you have to find out how many times this scenario occurs for all numbers up to N.

Examples:

      Number         Binary          Adjacent Bits

         12                    1100                        1

         15                    1111                        3

         27                    11011                      2

Input

Input starts with an integer T (≤ 10000), denoting the number of test cases.

Each case contains an integer N (0 ≤ N < 231).

Output

For each test case, print the case number and the summation of all adjacent bits from 0 to N.

Sample Input

7

0

6

15

20

21

22

2147483647

Sample Output

Case 1: 0

Case 2: 2

Case 3: 12

Case 4: 13

Case 5: 13

Case 6: 14

Case 7: 16106127360

详解：http://www.cnblogs.com/jianglangcaijin/archive/2012/10/10/2719029.html

好厉害，能这样找递推公式!!!!!!

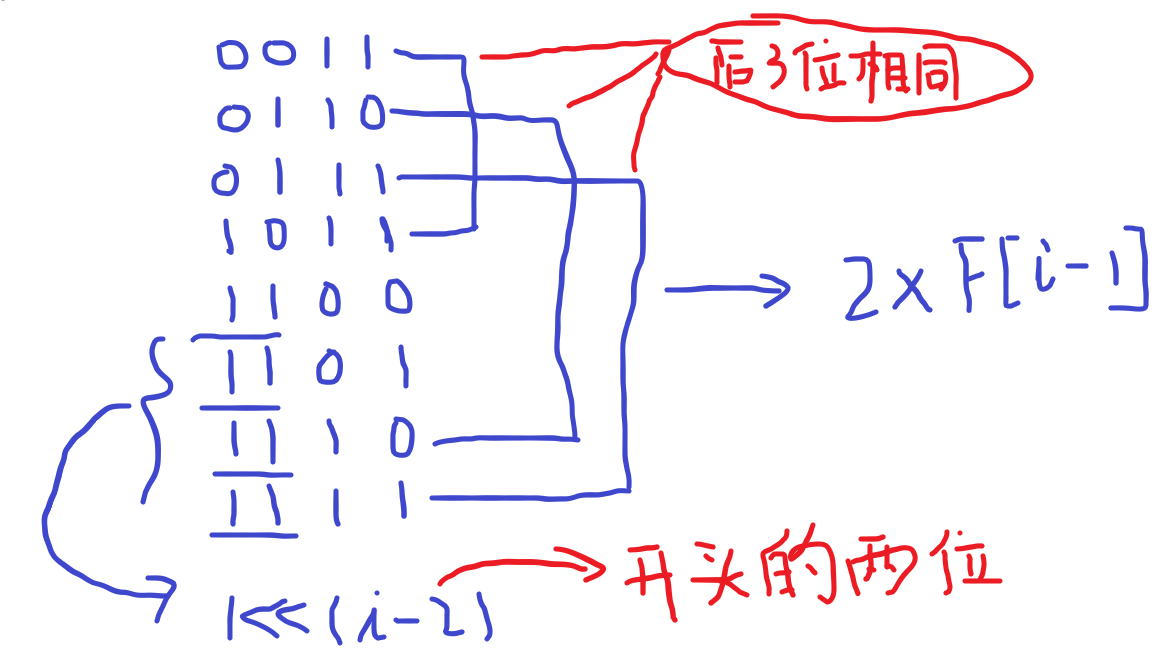
F[ i ]表示[ 0，(2^i)-1 ]这个区间上的数字的adjacent bits之和。

 

 

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 typedef long long ll;
 7 
 8 int n;
 9 ll F[40];
10 
11 void Inite(){
12     F[1]=0;F[2]=1;
13     for(int i=3;i<=31;i++) F[i]=F[i-1]*2+(1<<(i-2));
14 }
15 
16 ll Solve(int x){
17     ll ans=0;
18     for(int i=31;i>=0;i--){
19         if(x&(1<<i)){
20             x=x-(1<<i);
21             ans=ans+F[i]+max(0,x-(1<<(i-1))+1);
22         }
23     }
24     return ans;
25 }
26 
27 int main()
28 {   Inite();
29     
30     int kase;
31     cin>>kase;
32     for(int t=1;t<=kase;t++){
33         cin>>n;
34         printf("Case %d: %lld\n",t,Solve(n));
35     }
36     return 0;
37 }

 DP模式：

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 typedef long long ll;
 7 
 8 int n,num[40];
 9 ll dp[40][40][2];
10 
11 ll DFS(int pos,int sum,int pre,bool F){
12     if(pos==-1) return sum;
13     if(!F&&dp[pos][sum][pre]!=-1) return dp[pos][sum][pre];
14     
15     
16     int maxv=F?num[pos]:1;
17     ll ans=0;
18     for(int i=0;i<=maxv;i++){
19         if(pre&&i) ans=ans+DFS(pos-1,sum+1,i,F&&i==maxv);
20         else ans=ans+DFS(pos-1,sum,i,F&&i==maxv);
21     }
22     
23     if(!F) dp[pos][sum][pre]=ans;
24     return ans;
25 }
26 
27 ll Solve(int temp){
28     memset(dp,-1,sizeof(dp));
29     int cnt=0;
30     while(temp){
31         num[cnt++]=temp%2;
32         temp/=2;
33     }
34     return DFS(cnt-1,0,0,true);
35 }
36 
37 int main()
38 {   int kase;
39     cin>>kase;
40     for(int t=1;t<=kase;t++){ cin>>n; printf("Case %d: %lld\n",t,Solve(n)); }
41     return 0;
42 }

 

posted @ 2017-09-10 15:35  天之道，利而不害  阅读(215)  评论(0)  编辑  收藏  举报