傅里叶变换在多项式乘法中的应用（一）

\(A(x) = a_0 + a_1 x + a_2 x^2 + ··· + a_{n-1} x^{n-1}\)

求多项式的点值表达式

为了得到\(A(x)\)的点值表达式，选择一些比较特殊的\(x:=w_n^k\)，\(k \in \{0,1,2,···,n-1\}\)代入。

已知\(e^{i\theta} = cos \theta + i sin \theta\)

记 \(w_n^k = e^{i*(\frac{2\pi}{n}*k)} = cos(\frac{2\pi}{n}*k) + i sin(\frac{2\pi}{n}*k)\)，则\(w_n^{-k}\)表示\(w_n^k\)的共轭复数。

从向量角度看，\(w_n^k\)和复平面中与实轴正向夹角为\(\frac{2\pi}{n}*k\)的单位向量一一对应。

根据上面那个表达式可推得：

• \(w_{mn}^{mk} = w_n^k\)
• \(w_n^{k + \frac{n}{2}} = w_n^{-k}\)

先将\(A(x)\)按照\(x\)的阶的奇偶性分成两组，既：

\[\begin{aligned} A(x) &= (a_0 + a_2 x^2 + ··· + a_{n-2} x^{n-2}) + (a_1 x^1 + a_3 x^3 + ··· + a_{n-1} x^{n-1}) \\ &=(a_0 + a_2 x^2 + ··· + a_{n-2} x^{n-2}) + x(a_1 + a_3 x^2 + ··· + a_{n-1} x^{n-2}) \end{aligned} \]

令

\[A_1(x) = a_0 + a_2 x + ··· + a_{n-2} x^{\frac{n-2}{2}} \\ A_2(x) = a_1 + a_3 x + ··· + a_{n-1} x^{\frac{n-2}{2}} \]

则

\[A(x) = A_1(x^2) + xA_2(x^2) \]

当\(x = w_n^k\)，\(k \in \{0,1,2,···,\frac{n}{2} - 1\}\)，有

\[\begin{aligned} A(w_n^k) &= A_1((w_n^k)^2) + w_n^k*A_2((w_n^k)^2) \\ &= A_1(w_n^{2k}) + w_n^k * A_2(w_n^{2k}) \\ &= A_1(w_{\frac{n}{2}}^k) + w_n^k * A_2(w_{\frac{n}{2}}^k) \end{aligned} \]

当\(x = w_n^{k + \frac{n}{2}}\)，\(k \in \{0,1,2,···,\frac{n}{2} - 1\}\)，有

\[\begin{aligned} A(w_n^{k + \frac{n}{2}}) &= A_1((w_n^{k + \frac{n}{2}})^2) + w_n^{k + \frac{n}{2}} * A_2((w_n^{k + \frac{n}{2}})^2) \\ &= A_1(w_n^{2k + n}) + w_n^{k + \frac{n}{2}} * A_2(w_n^{2k + n}) \\ &= A_1(w_n^{2k + n}) - w_n^k * A_2(w_n^{2k + n}) \\ &= A_1(w_n^{2k}) - w_n^k * A_2(w_n^{2k}) \\ &= A_1(w_{\frac{n}{2}}^k) - w_n^k * A_2(w_{\frac{n}{2}}^k) \end{aligned} \]

如果已知\(A_1(x)\)和\(A_2(x)\)在\(x = w_{\frac{n}{2}}^k\)，\(k \in \{0,1,2,···,\frac{n}{2} - 1\}\)处的值，那么就可以在\(O(n)\)的时间内求得\(A(x)\)的点值表达式：\(((w_n^0,A(w_n^0)),(w_n^1,A(w_n^1)),···,(w_n^{n-1},A(w_n^{n-1})))\)。

求解\(A_1(x)\)和\(A_2(x)\)在\(x = w_{\frac{n}{2}}^k\)，\(k \in \{0,1,2,···,\frac{n}{2} - 1\}\)处的值与求解\(A(x)\)在\(x = w_n^k\)，\(k \in \{0,1,2,···, n-1\}\)处的值的过程是一样的，只是规模减少了一半，运用递归分析法可概括得：

\[\begin{aligned} T(n) &= 2T(\frac{n}{2}) + O(n) \\ &=O(nlg(n)) \end{aligned} \]

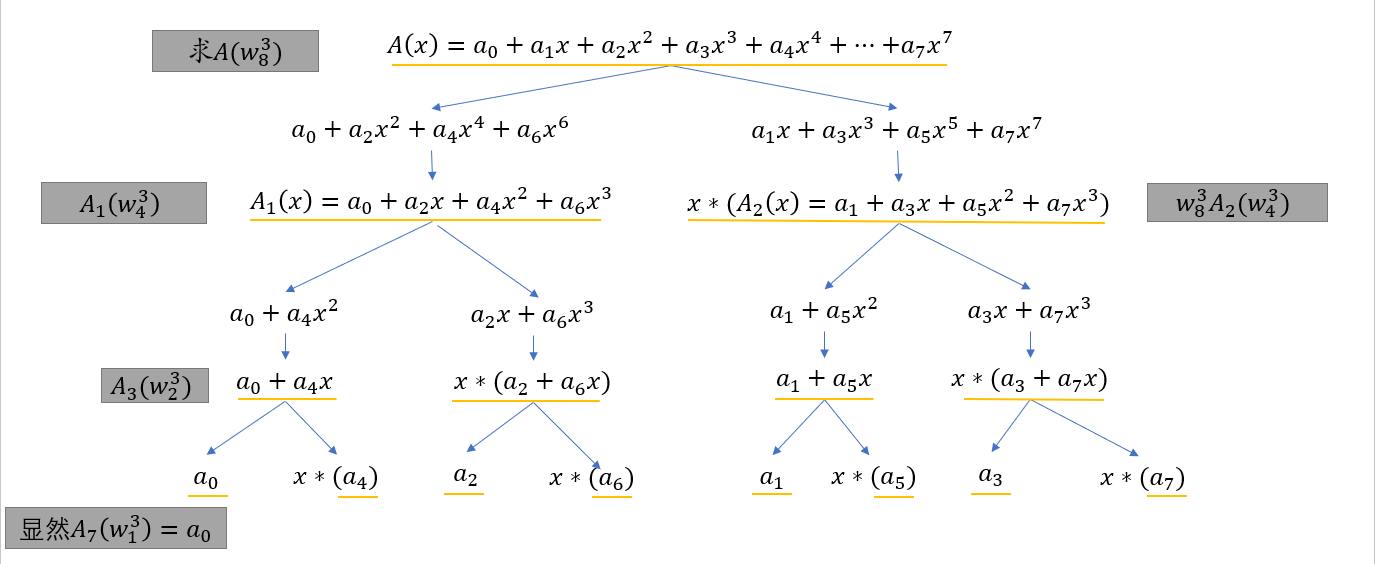
拿个多项式模拟一下上述表达式蕴含的递归过程，如图：

code

struct complex_number {
    double a, b;
    complex_number() { a = 0, b = 0; }
    complex_number(double a, double b): a(a), b(b) {}

    complex_number operator + (const complex_number& o) const {
        return complex_number(a + o.a, b + o.b);
    } 
    complex_number operator - (const complex_number& o) const {
        return complex_number(a - o.a, b - o.b);
    }
    complex_number operator * (const complex_number& o) const {
        return complex_number(a * o.a - b * o.b, a * o.b + b * o.a);
    }
    complex_number complex_conjugate() {
        return complex_number(a, -b);
    }
};

const int maxn = 100005;

complex_number cn[maxn];

complex_number w(int n, int k) {
    return complex_number(cos(2 * atan(1) * 4.0 * k / n), sin(2 * atan(1) * 4.0 * k / n));
}

void DFT(complex_number* A, int n) {
    if (n == 1) return;

    const int m = n >> 1;
    static complex_number buf[maxn];   

    for (int i = 0; i < m; i++) {
        buf[i] = A[i << 1];
        buf[i + m] = A[i << 1 | 1];
    }

    memcpy(A, buf, sizeof(complex_number) * n);

    complex_number *A1 = A, *A2 = A + m;

    DFT(A1, m);
    DFT(A2, m);

    for (int i = 0; i < m; i++) {
        complex_number temp = w(n, i);
        buf[i] = A1[i] + temp * A2[i];
        buf[i + m] = A1[i] - temp * A2[i];
    }

    memcpy(A, buf, sizeof(complex_number) * n);
}

---

点值表达式 \(\rightarrow\) 系数表达式 [ Inverse Discrete Fourier Transform ]

假设 \(d_k = A(w_n^k) = \sum_{i=0}^{n-1}a_i (w_n^k)^i\)，\(k \in \{0,1,2,···, n-1\}\)，构造如下多项式：

\[F(x) = d_0 + d_1 x^1 + d_2 x^2 + ··· + d_{n-1} x^{n-1} \]

假设 \(c_k = F(w_n^{-k}) = \sum_{i = 0}^{n-1}d_i(w_n^{-k})^i\)，\(k \in \{0,1,2,···,n-1\}\)，展开\(d_i\)得：

\[\begin{aligned} c_k &= \sum_{i=0}^{n-1}[\sum_{j=0}^{n-1}a_j(w_n^i)^j] *(w_n^{-k})^i \\ &= \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(w_n^i)^j(w_n^{-k})^i \\ &= \sum_{j=0}^{n-1}\sum_{i=0}^{n-1}a_j(w_n^i)^j(w_n^{-k})^i & 交换求和顺序 \\ &= \sum_{j=0}^{n-1}a_j[\sum_{i=0}^{n-1}(w_n^i)^j(w_n^{-k})^i] \\ &= \sum_{j=0}^{n-1}a_j[\sum_{i=0}^{n-1}(w_n^{i})^{j-k}] \\ &= \{\sum_{j=0,j\neq k}^{n-1}a_j[\sum_{i=0}^{n-1}(w_n^{i})^{j-k}]\} + \{a_k[\sum_{i=0}^{n-1}(w_n^{i})^{0}]\} \\ &= \{\sum_{j=0,j\neq k}^{n-1}a_j[\sum_{i=0}^{n-1}(w_n^{i})^{j-k}]\} +n*a_k \end{aligned} \]

当\(j \neq k\)时，令\(j - k = \theta\)，有：

\[\begin{aligned} \{\sum_{j=0,j\neq k}^{n-1}a_j[\sum_{i=0}^{n-1}(w_n^{i})^{\theta}]\} &= \sum_{j=0,j\neq k}^{n-1}a_j(w_n^0 + w_n^{\theta} + w_n^{2\theta}+···+ w_n^{(n-1)\theta}) \\ &= \sum_{j=0,j\neq k}^{n-1}a_j(\frac{w_n^0(1-(w_n^{\theta})^n)}{1-w_n^{\theta}}) & 等比公式 \\ &= \sum_{j=0,j\neq k}^{n-1}a_j(\frac{1-(w_n^n)^{\theta}}{1-w_n^{\theta}}) \\ &= \sum_{j=0,j\neq k}^{n-1}a_j(\frac{1-(1)^{\theta}}{1-w_n^{\theta}}) \\ &= \sum_{j=0,j\neq k}^{n-1}a_j(\frac{0}{1-w_n^{\theta}}) \\ &= 0 \end{aligned} \]

故

\[\begin{aligned} c_k &= n * a_k \\ a_k &= \frac{c_k}{n} \end{aligned} \]

所以只要求得了\(F(x)\)的点值表达式：\(((w_n^0, c_1), (w_n^{-1}, c_2), ···, (w_n^{-(n-1)},c_{n-1}))\)，那么就可以在\(O(n)\)的时间内求得\(F(x)\)的系数表达式：\((a_0, a_1, a_2, ···, a_{n-1})\)。

参考

• 一小时学会快速傅里叶变换（Fast Fourier Transform） - 白空谷的文章 - 知乎
  https://zhuanlan.zhihu.com/p/31584464