B+树实现
B+树实现
节点特征
典型的B+树节点如图所示,有 \(n - 1\) 个键值,\(n\) 个指针,且如果 \(i < j\),有 \(K_i < K_j\)。

B+树中的节点分为两类:内部节点和叶子节点,区别在于叶子节点的指针指向实际存在的记录,且\(P_n\)指向相邻的叶子节点,既叶子节点组成了一个单链表。显然,单链表方便了记录的顺序查找。
具体实现:
class node {
private:
int cnt, key[MAX];
NODE_TYPE m_type;
public:
node();
virtual ~node();
void Error(int lind);
int Size();
int cnt_increase();
int cnt_decrease();
void set_key(int id, int x);
int get_key(int id);
void set_type(NODE_TYPE te);
NODE_TYPE Type();
int pos(int k); // 查找第一个大于或等于 K 的位置
int get_middle_key(); // 节点分裂的时候需要将中间位置的键值向上插到父节点中
};
class Internal_node: public node {
private:
node* pointer[MAX];
public:
Internal_node();
~Internal_node();
void set_pointer(int id, node* p);
node* get_pointer(int id);
/*
假设 k 插入的位置是 i
p 插入的位置是j
一定满足:j = i + 1
*/
void Insert(int k, node* p);
Internal_node* split();
void Merge(Internal_node* brother_node, int x);
void Delete(int pos);
void right_shift_one_position();
void left_shift_one_position();
void borrow_from_left_brother(Internal_node* left_brother, int x);
void borrow_from_right_brother(Internal_node* right_brother, int x);
};
class Leaf_node: public node{
private:
int value[MAX];
Leaf_node* next;
public:
Leaf_node();
~Leaf_node();
void set_value(int id, int x);
int get_value(int id);
void set_next(Leaf_node* np);
Leaf_node* get_next();
void Insert(int k, int va);
Leaf_node* Split();
void Merge(Leaf_node* brother_node);
void Delete(int pos);
void right_shift_one_position();
void left_shift_one_position();
void borrow_from_left_brother(Leaf_node* left_brother);
void borrow_from_right_brother(Leaf_node* right_brother);
}
插入功能
根据B+树的定义,叶子节点的指针才指向实际存储的记录。插入一个键值对,需要先遍历到对应的叶子节点。如果该叶子节点已经满了,插入键值后,叶子节点分裂为两个节点。如果该叶子节点没满,插入键值后返回。显然,这个过程是递归的,叶子节点分裂可能会导致它的父节点分裂(因为上传了一个键值),父节点分裂可能会导致父节点的父节点分裂,直到分裂到根节点。
具体实现:每个节点遵守相同的顺序,先插入键值,再分裂。
笔者的写法是:当前节点插入键值,递归到其父节点时才判断当前节点是否过满。过满则分裂当前节点。显然,这样写需要单独判断根节点是否过满。
void Bplus_tree:: m_insert(node* cur, int k, int v) {
if (cur->Type() == LEAF) {
((Leaf_node*)cur)->Insert(k, v);
return;
}
else {
int pos = cur->Pos(k);
node* next_pointer = ((Internal_node*)cur)->get_pointer(pos);
m_insert(next_pointer, k, v);
if (next_pointer->Size() > MAX_KEY_NUMBER) {
int up_key = next_pointer->get_middle_key();
node* new_node = nullptr;
if (next_pointer->Type() == LEAF) {
new_node = ((Leaf_node*)next_pointer)->Split();
((Leaf_node*)new_node)->set_next(((Leaf_node*)next_pointer)->get_next());
((Leaf_node*)next_pointer)->set_next(((Leaf_node*)new_node));
}
else {
node* new_node = ((Internal_node*)next_pointer)->Split();
}
((Internal_node*)cur)->Insert(up_key, new_node);
}
}
}
删除功能
同样,删除一个键值对也需要遍历到叶子节点。删除该键值对后,如果叶子节点非半满,则向左兄弟或者右兄弟借一个键值,如果借不到,则与左兄弟或者右兄弟合并,并下拉父节点中对应的键值(叶子节点的合并不需要下拉键值)。如果能借到,则调整键值和指针(叶子节点和内部节点的调整过程不同)。显然这个过程也是递归的,节点的合并可能会导致根节点的消失。
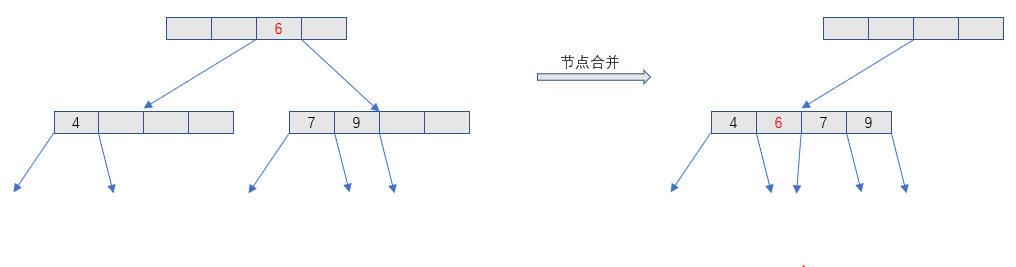
如果删除的键值在内部节点(非叶子节点)出现过,则删除过程稍微复杂一点。记删除的键值为\(K\),含有\(K\)的内部节点为\(u\),\(K\)在节点\(u\)中的下标为\(i\),则\(P_{i + 1}\)指向的节点为\(v\)。记以\(v\)为根的子树中的最小键值为\(v_{min}\)。当递归回到\(u\)节点时,先用\(v_{min}\)替换掉\(K\),再执行原来的删除过程。
void Bplus_tree:: m_delete(node* cur, int k, int v) {
if (cur->Type() == LEAF) {
int pos = cur->Pos(k);
if (((Leaf_node*)cur)->get_value(pos) == v) {
((Leaf_node*)cur)->Delete(pos);
return;
}
}
else {
int pos = cur->Pos(k), flag = 0, replace_key = -2;
if (cur->get_key(pos) == k) flag = 1;
node* next_pointer = ((Internal_node*)cur)->get_pointer(pos + flag);
m_delete(next_pointer, k, v);
if (next_pointer->Size() * 2 < MAX_KEY_NUMBER) {
node* left_brother = ((pos + flag) == 0 ? nullptr : ((Internal_node*)cur)->get_pointer(pos + flag - 1));
node* right_brother = ((pos + flag) == cur->Size() ? nullptr : ((Internal_node*)cur)->get_pointer(pos + flag + 1));
if (left_brother->Size() * 2 > MAX_KEY_NUMBER) {
int n = left_brother->Size();
int down_key = cur->get_key(pos + flag - 1);
cur->set_key(pos + flag - 1, left_brother->get_key(n - 1));
/*
首先判断节点类型,不同节点类型执行的操作稍微不同
然后判断要删除的键是不是在内部节点出现过
*/
if (left_brother->Type() == LEAF) {
((Leaf_node*)next_pointer)->borrow_from_left_brother(((Leaf_node*)left_brother));
}
else {
if (flag) {
replace_key = m_find_replaceOfkey(cur, k);
if (replace_key == -1) cur->Error(__LINE__);
((Internal_node*)next_pointer)->borrow_from_left_brother(((Internal_node*)left_brother), replace_key);
}
else {
((Internal_node*)next_pointer)->borrow_from_left_brother(((Internal_node*)left_brother), down_key);
}
}
}
else if (right_brother->Size() * 2 > MAX_KEY_NUMBER) {
int down_key = cur->get_key(pos + flag);
if (right_brother->Type() == LEAF) {
cur->set_key(pos + flag, right_brother->get_key(1));
((Leaf_node*)next_pointer)->borrow_from_right_brother(((Leaf_node*)right_brother));
if (flag) {
cur->set_key(pos, next_pointer->get_key(0));
}
}
else {
if (flag) {
replace_key = m_find_replaceOfkey(cur, k);
if (replace_key == -1) cur->Error(__LINE__);
cur->set_key(pos + flag, right_brother->get_key(0));
((Internal_node*)next_pointer)->borrow_from_right_brother(((Internal_node*)right_brother), down_key);
cur->set_key(pos, replace_key);
}
else {
cur->set_key(pos, right_brother->get_key(0));
((Internal_node*)next_pointer)->borrow_from_right_brother(((Internal_node*)right_brother), down_key);
}
}
}
else if (left_brother != nullptr) {
if (left_brother->Type() == LEAF) {
((Leaf_node*)left_brother)->set_next(((Leaf_node*)next_pointer)->get_next());
((Leaf_node*)left_brother)->Merge(((Leaf_node*)next_pointer));
}
else {
if (flag) {
replace_key = m_find_replaceOfkey(cur, k);
((Internal_node*)left_brother)->Merge(((Internal_node*)next_pointer), replace_key);
}
else {
int down_key = cur->get_key(pos - 1);
((Internal_node*)left_brother)->Merge(((Internal_node*)next_pointer), down_key);
}
}
((Internal_node*)cur)->Delete(pos + flag - 1);
}
else if (right_brother != nullptr) {
if (next_pointer->Type() == LEAF) {
((Leaf_node*)next_pointer)->set_next(((Leaf_node*)right_brother)->get_next());
((Leaf_node*)next_pointer)->Merge(((Leaf_node*)right_brother));
}
else {
if (flag) {
replace_key = m_find_replaceOfkey(cur, k);
((Internal_node*)next_pointer)->Merge(((Internal_node*)right_brother), replace_key);
}
else {
int down_key = cur->get_key(pos);
((Internal_node*)next_pointer)->Merge(((Internal_node*)right_brother), down_key);
}
}
((Internal_node*)cur)->Delete(pos);
}
else {
cur->Error(__LINE__);
return;
}
}
else {
if (flag) {
replace_key = m_find_replaceOfkey(cur, k);
cur->set_key(pos, replace_key);
}
}
}
}


