HDU 3068

题意

给一个字符串\(s\)，求最长回文子串

题解

马拉车算法的模板题。
首先，预处理字符串\(s\)，在每个字符的左边和右边都插上一个特殊符号，比如#，目的是保证字符串的长度为奇数。举例来说，abc \(\rightarrow\) #a#b#c#，abcd \(\rightarrow\) #a#b#c#d#。同时为了保证\(while\)循环不超边界，需要在处理后的字符串的头尾加上不相同的特殊字符。举例来说，#a#b#c# \(\rightarrow\) @#a#b#c#$。（如果声明的是全局变量，则末尾不用插特殊字符，因为在声明的时候，已经被初始化：0）
然后，令\(id:=\) 先前已经找到的所有回文串中边界最远的回文串 的中心，\(mx:=\)先前已经找到的所有回文串中边界最远的回文串 的边界。分类讨论：

• \(i <= mx\)，\(p[i] = min(mx - i + 1, p[2 * id - i])\)。因为\(i\)关于\(id\)的对称点\(j\)（\(j = 2 * id - i\)）的回文串的长度已经知道，所以\(p[i] = p[j]\)可能成立。如果\(i + p[i] - 1 > mx\)，那么超过\(mx\)的那部分字符串可能不是以\(i\)为中心的回文串的一部分。这就是为啥这儿要取\(min\)
• \(i > mx\)，就用最朴素的方法，找\(i\)为中心的最长回文串

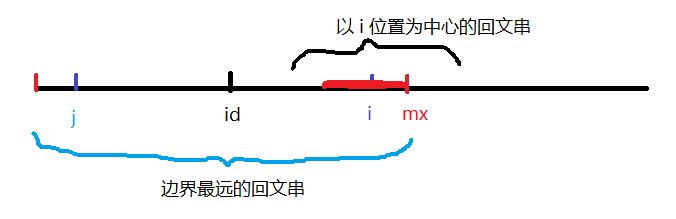
最后，在更新\(p[i]\)的过程中记录最大\(p[i] - 1\)就行

int p[MAXN * 2];
char ma[MAXN * 2];

int Mana(char* s, int n) {
    
    int m = 1;
    // inite string s
    ma[0] = '@';
    for (int i = 0; i < n; ++i) {
        ma[m++] = '#';
        ma[m++] = s[i];
    }
    ma[m] = '#';

    //printf("%s\n", ma);

    int id = 0, mx = 0, ans = 0;
    for (int i = 0; i < m; ++i) {
        if (i < mx) p[i] = min(mx - i + 1, p[2 * id - i]);
        else p[i] = 1;
        while(ma[i - p[i]] == ma[i + p[i]]) p[i]++;
        if (i + p[i] - 1 > mx) {
            id = i;
            mx = i + p[i] - 1;
            ans = max(ans, p[i] - 1);
        }
    }

    return ans;
}