《Neural Network and Deep Learning》_chapter4

《Neural Network and Deep Learning》_chapter4: A visual proof that neural nets can compute any function文章总结(前三章翻译在百度云里)

链接：http://neuralnetworksanddeeplearning.com/chap4.html；

Michael Nielsen的《Neural Network and Deep Learning》教程中的第四章主要是证明神经网络可以用来表示任何一种函数映射

 现在对这篇文章进行一下梳理：作者首先提出了两点注意：

（1）神经网络并不是给出函数映射的一个准确的结果，而是一个近似值；

（2）神经网络表示的一种连续函数映射，无法实现非连续的函数映射。

然后作者开始证明神经网络的这种性质的普遍性，

（一）单输入/单输出的情况着手开始证明：

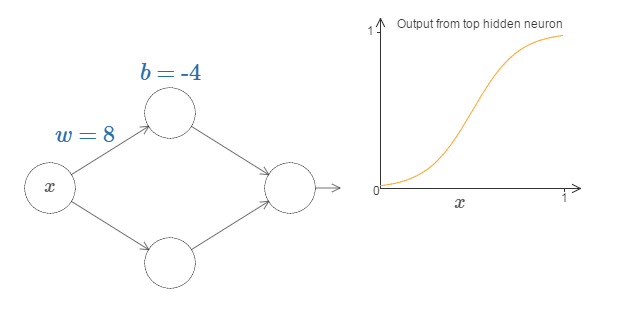
上图，权值是8，阈值是-4，激活函数为sigmoid函数。隐藏层的输出近似为右图，当我们令权值w足够大时，隐藏层神经元的输出近似为阶跃函数，如下：

上图中，阶跃位置s=-b/w,现证明如下：

设阶跃位置是A点，则

并且我们有如下结论：改变阈值使输出曲线平移，改变权值会使图像陡峭/平滑；

之所以我们在这里要使隐藏层神经元的输出近似为阶跃函数，是因为这样神经元的输出不是0就是1，这样再传到输出层计算误差小，更加拟合期望的函数映射，而如果是S型曲线，则计算误差大，难以拟合期望的输出曲线（这里是我自己的理解，欢迎讨论）

上图中，阶跃位置分别为s1=0.4,s2=0.6,阶跃函数的最终值分别为0.6和1.2,所以最终的输出曲线如右图，这里改变s1和s2的位置即改变了神经元们被激活的顺序，这样也就改变了输出的形状；

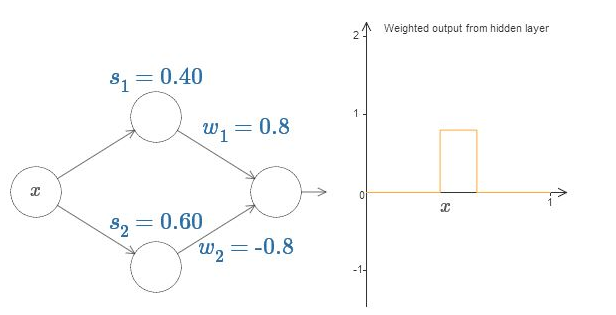
上图中令w1=-w2=0.8,输出即为高为0.8的bump 函数（肿块函数），从0.4到0.6；

上图中的输出还可以用下图的"if-then-else"来解释：

即x>阶跃位置，则输出为1，反之为0；

增加隐藏层神经元的数目，就可以n个这样的bump函数来近似我们想要的函数映射，如下：

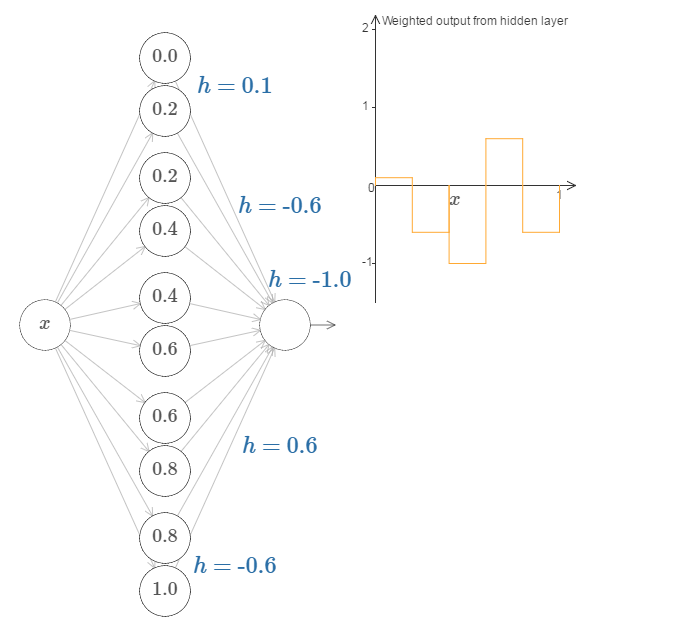
类似于微积分的原理。。。。

我们的目的就是设计这样一种神经网络使实际输出与期望的函数映射之间的平均误差最小化；

我们可以使用上面的方法实现任何一种[0,1]到[0,1]的映射（我觉得应该不限于[0,1]到[0,1]的映射）；

 （二）对于多输入时普遍性的证明：

先从两个输入时的情况着手：

上图中连接x的权值足够大，连接y的权值为0，隐藏层神经元的阶跃位置为0.5，上图中的曲线只会在x方向上进行移动（隐藏层神经元上方的x表示移动的方向为x方向）；类似地，令连接y的权值足够大，连接x的权值为0，则输出曲线只会在Y方向上移动；

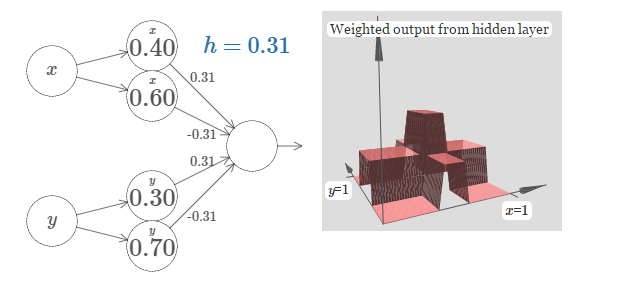
上图中，plateau(平台)的高为h,中心tower(塔)的高为2h(h+h)，我们需要实现下面这种tower function:

再参考之前的"if-then-else"法则我们有：

这里令threshold为3h/2，则plateau的值变为0，中心tower的值变为1.从而可获得tower function.而实际操作时我们可以这样做：

加入阈值b和sigmoid激活函数：

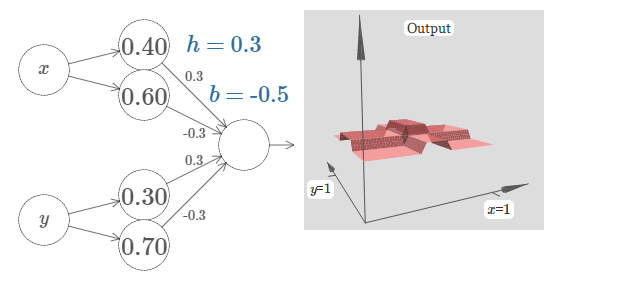
想要获得tower函数，我们一般令h足够大，b为（-m+0.5）h(经验值)，其中m是输入变量的个数：

后面的Problem这里只证明(a),另外两题略；

证明神经网络的普遍性之后，作者关于sigmoid函数又做了一些额外说明：

（1）线性激活函数无法实现上面的普遍性，因为它无法实现阶跃函数那样的形状；

（2）作者在这儿提到了Failure Windows一概念，即下图中的绿色部分：

我们的目的就是令Failure Windows尽可能的小，一种方法就是用M个σ^-1°f(x)/M函数进行叠加，M越大，Failure Windows就会变得更狭窄。