从boosting角度理解softmax
转载的这篇文章来自峰神知乎上的文章，链接如下：
Softmax理解之二分类与多分类 - 王峰的文章 - 知乎 https://zhuanlan.zhihu.com/p/45368976
本文首先分析了softmax的性质，然后得出了softmax可以看成 "多个二分类器加权结合" 的方法，具体内容如下：
本篇为Softmax理解的第二篇文章，没看过第一篇的请点击传送门：从最优化的角度看待Softmax损失函数 。
在SVM时代，因为SVM是一个二分类器，如果我们要进行多分类，就需要使用1 vs 1或者1 vs all的技巧来训练。其中1 vs 1需要寻找两两组合的 个分界面；而1 vs all需要训练
个分类器，寻找的是某个类别与其他所有类别之间的分界面。具体的情况可以看看这篇博客：支持向量机SVM整理 - CSDN博客 。
神经网络时代用得最多的是Softmax交叉熵损失函数，它是从逻辑回归这个二分类器上演化出来的，具体是如何演化的可以看看这个教程：http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92。注意这里提到了因为Softmax操作是有冗余的，所以在二分类情况下Softmax交叉熵损失等价于逻辑回归。但实际上Softmax是给每个类别都分配了权重向量，而逻辑回归和SVM都是只有一个向量来表示这两个类别之间的分界面。如果我们强行还要使用Softmax进行二分类，那么根据公式（假设当前样本的类别为1）
，
其中 ，可以推导出
得到的梯度永远是反向且幅度是相等的。这两个类别之间的分界面就是
。
Softmax交叉熵损失函数的核心在于Softmax操作，它将样本在 个类别的分数
转化成了一组概率值
：
这一组概率具备概率的各种性质，这篇文章主要用到两个性质：
1、非负性： ；
2、正则性： 。
Softmax交叉熵损失函数关于分数 的导数如下：
这个导数的含义是：对于目标分数 ，其梯度为负数
，其他的非目标分数得到的梯度恰好为其对应的概率值
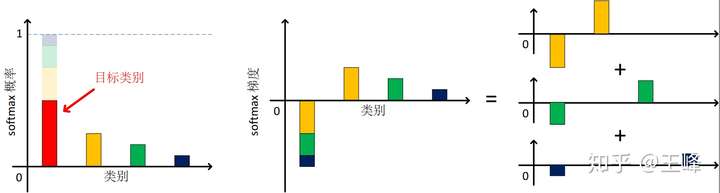
。我将Softmax的概率和梯度的关系画在了题图中，从这张图上可以总结出以下性质：
1、Softmax交叉熵损失对分数的梯度之和为0，即 ；
2、Softmax交叉熵损失对各个分数的梯度绝对值之和为2倍的对目标分数梯度绝对值之和，即 ；
3、Softmax交叉熵损失对非目标分数的梯度之和等于对目标分数梯度的绝对值,即 ；
其中第1条性质说明回传的正负梯度之间是平衡的，第2条性质说明回传梯度的总幅度是受限的，这两条性质保证了Softmax loss不会出现上一篇文章提到的Hinge loss那样的非目标分数得到的梯度过多的情况。
这里的第3条性质比较重要，我把它画在了题图的右图上，根据这条性质，对目标分数 的梯度可以被分解为
份，每一份与对应的非目标分数
的梯度都可以组成一对正负梯度，这对梯度反向且幅度相等，刚好符合我们前面分析的二分类器的性质。因此，对于每一个类别，Softmax实际上是训练了
个二分类器的线性组合，而这
个二分类器的权重恰好等于非目标概率
。
这与SVM的1 vs 1方式比较类似，区别在于SVM训练的是分界面而不是类别向量，所以SVM需要训练 个分界面，但Softmax只需要训练
个类向量即可。这些类别的分界面可以由
来求得，仍然可以得到类似的
个分界面。所以Softmax是比SVM 1 vs 1更省空间也更省计算量的多分类器。最关键的是，Softmax的多个分类器是同时训练的，因此其效率远远超过了需要训练多次的SVM。
另一个区别在于权重的分配，Softmax的各个二分类器之间的权重分配遵循了“较难的二分类器给予较大权重”的原则，其中难易的准则是由当前样本的分类情况来决定的，如果某个非目标分数较高则认为当前样本对于这个类别的区分能力较差，要着重优化这个非目标分数。而且Softmax概率是经过了指数函数的，因此较难的二分类器可以获得远超已经分得比较好的分类器的权重。
总结一下，Softmax交叉熵损失函数在进行多分类时可以理解为是在训练多个二分类器的组合，只不过因为Softmax训练的是类别向量而不是分界面，所以其训练效率得到了很大的提升。Softmax交叉熵损失函数的多条优良的性质以及它在多个二分类器之间的权重分配方式有助于我们设计其他的损失函数，同时也能启发一下多个损失函数之间加权方式的研究，毕竟Softmax看似是多分类，实际上是有着巧妙设计的权重的多个二分类器，那么其他的多损失函数说不定也能利用一下类似的权重分配方式呢？
