RNN梯度消失&爆炸原因解析与LSTM&GRU的对其改善
一、关于RNN的梯度消失&爆炸问题
1. 关于RNN结构
循环神经网络RNN（Recurrent Neural Network）是用于处理序列数据的一种神经网络，已经在自然语言处理中被广泛应用。下图为经典RNN结构：
2. 关于RNN前向传播
RNN前向传导公式：
其中: St : t 时刻的隐含层状态值
Ot : t 时刻的输出值
① 是隐含层计算公式，U是输入x的权重矩阵，W是时刻t-1的状态值
St-1作为输入的权重矩阵，Φ是激活函数。
② 是输出层计算公式，V是输出层的权重矩阵，f是激活函数。
损失函数（loss function）采用交叉熵
（ Ot 是t时刻预测输出， 
是 t 时刻正确的输出）
那么对于一次训练任务中，损失函数：
， T 是序列总长度。
假设初始状态St为0，t=3 有三段时间序列时，由 ① 带入②可得到
t1、t2、t3 各个状态和输出
3. 关于RNN反向传播
BPTT（back-propagation through time）算法是针对循层的训练算法，它的基本原理和BP算法一样。其算法本质还是梯度下降法，那么该算法的关键就是计算各个参数的梯度，对于RNN来说参数有 U、W、V。
反向传播
可以简写成：
观察③④⑤式，可知，对于 V 求偏导不存在依赖问题；但是对于 W、U 求偏导的时候，由于时间序列长度，存在长期依赖的情况。主要原因可由 t=1、2、3 的情况观察得 , St会随着时间序列向前传播，同时St是 U、W 的函数。
前面得出的求偏导公式⑥，取其中累乘的部分出来，其中激活函数 Φ 通常是：tanh 则
由上图可知当激活函数是tanh函数时，tanh函数的导数最大值为1，又不可能一直都取1这种情况,而且这种情况很少出现，那么也就是说，大部分都是小于1的数在做累乘，若当t很大的时候，
趋向0，举个例子：0.850=0.00001427247也已经接近0了，这是RNN中梯度消失的原因。
但要注意：RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。
再看⑦部分：
tanh’，还需要网络参数 W ，如果参数 W 中的值太大，随着序列长度同样存在长期依赖的情况，那么产生问题就是梯度爆炸，而不是梯度消失了，在平时运用中，RNN比较深，使得梯度爆炸或者梯度消失问题会比较明显。
二、LSTM缓解梯度消失
至于怎么避免这种现象，让我在看看 梯度消失和爆炸的根本原因就是
这一坨，要消除这种情况就需要把这一坨在求偏导的过程中去掉，至于怎么去掉，一种办法就是使
另一种办法就是使
。其实这就是LSTM做的事情。
我们来看看LSTM的内部结构，包含了四个门层结构：
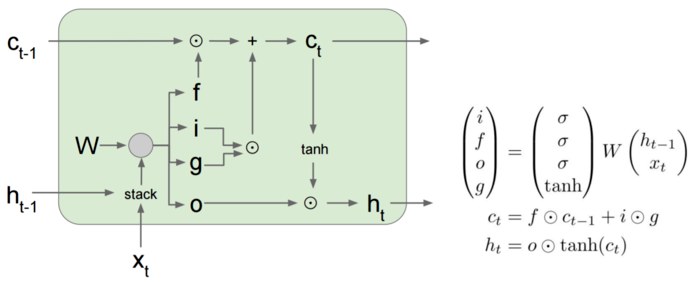引用自 Stanford CS231n slides
LSTM相信很多人看过这个：[译] 理解 LSTM 网络，但是我发现cs231n的公式更加简洁，把四个门层结构的权重参数合成一个W。
求导过程比较复杂，我们先看一下这一项：
和前面一样，我们来求一下 ，这里注意
，
和
都是
的复合函数：
后面的我们就不管了，展开求导太麻烦了，第一项是什么！大声告诉我！
是forget gate的输出值，1表示完全保留旧状态，0表示完全舍弃旧状态，那如果我们把
设置成1或者是接近于1，那
这一项就有妥妥的梯度了。
因此LSTM是靠着cell结构来保留梯度，forget gate控制了对过去信息的保留程度，如果gate选择保留旧状态，那么梯度就会接近于1，可以缓解梯度消失问题。这里说缓解，是因为LSTM只是在 到
这条路上解决梯度消失问题，而其他路依然存在梯度消失问题。
而且forget gate解决了RNN中的长期依赖问题，不管网络多深，也可以记住之前的信息。
另外，LSTM可以缓解梯度消失，但是梯度爆炸并不能解决，但实际上前面也讲过，梯度爆炸不是什么大问题（阈值裁剪）。
三、GRU缓解梯度消失
LSTM内部结构比较复杂，因此衍生了简化版GRU，把LSTM的input gate和forget gate整合成一个update gate，也是通过gate机制来控制梯度：
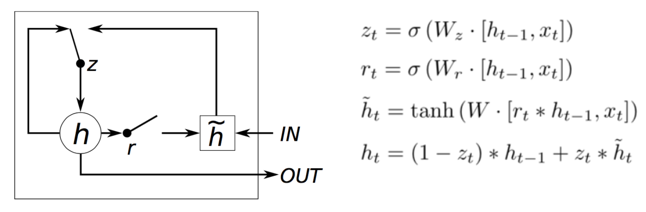
我们还是来求一下 ，我们可以得到：
，那一串省略号我们还是不管，我们依然可以通过控制
来控制梯度。
所以，我们现在可以看到，LSTM系列都是通过gate机制来缓解梯度消失问题的。
