Codeforces Round #793 D. Circular Spanning Tree(构造）

思路：首先讨论点的度数，整个点的度数应该都是偶数的（每条边贡献两度），那就意味这奇数点的个数是偶数

所以奇数点的个数是奇数的直接输出NO

接下来则讨论如何构造不存在交叉边的图

对于这样一个图

 

 要构造所有边都尽量不相邻的方法是

 

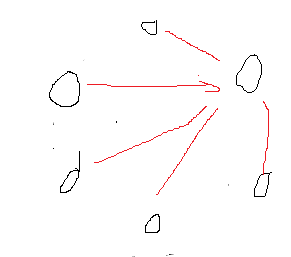
 即一个类似树的结构，我们很自然会想到构建一个树

为了保证偶数点的的度为偶数，我们可以将它们串联成一条链，链尾是奇数点（即叶子节点）

之后则是随机找一个偶数点作为树的顶点

链条个数取决于奇数点个数，所以保证顶点度数不会被改变

AC代码：

#pragma GCC optimize(2)
#pragma GCC optimize(1)
#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
const ull base=131;
#define MAX 1009
#define PI 3.141592653589793
using namespace std;
inline void solve(){
    int len;
    string op;
    cin>>len>>op;op=" "+op;
    int c=0;
    for(int i=1;i<=len;i++) if(op[i]=='1')c++;
    if(c%2||c<2){
        cout<<"No"<<"\n";return;
    }
    cout<<"Yes\n";
    vector<pair<int,int>> edge;//存边
    vector<int> lank[len+3];
    int beg=1;
    int num=1,time=0;
    for(;beg<=len;beg++) if(op[beg]=='1')break;//记录第一个1的位置
    while(1){
        while(1){
            lank[num].push_back(beg);
            if(beg<len) beg++;
            else beg=1;
            time++;
            if(op[beg]=='1'||time==len) break;
        }
        reverse(lank[num].begin(), lank[num].end());
        if(time==len) {
            break;
        }
        num++;
    }
    int txt=lank[num][0];
    for(int i=1;i<num;i++){
        edge.push_back({lank[i][0],txt});
    }
    for(int i=1;i<=num;i++){
        int si=lank[i].size();
        for(int j=0;j<si-1;j++){
            edge.push_back({lank[i][j],lank[i][j+1]});
        }
    }
    int all=edge.size();
    for(int i=0;i<all;i++) cout<<edge[i].first<<' '<<edge[i].second<<"\n";
   
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int sum;cin>>sum;
    while(sum--){
        solve();
    }
}