欧拉降幂

 

 

 

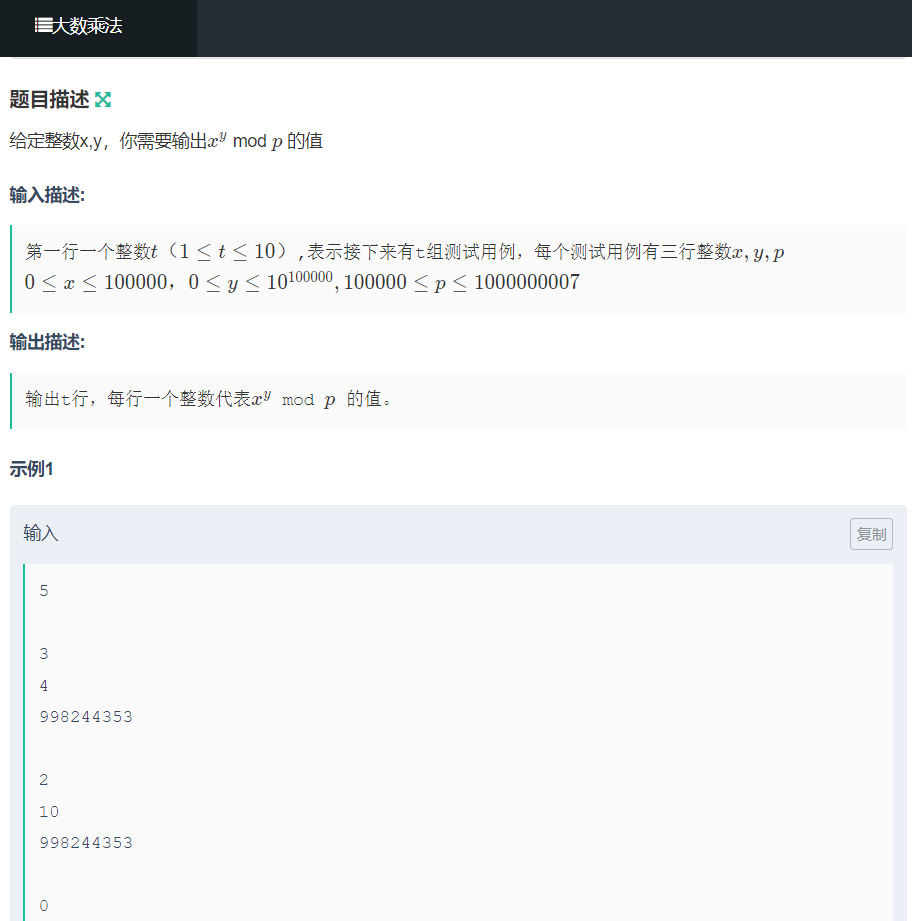
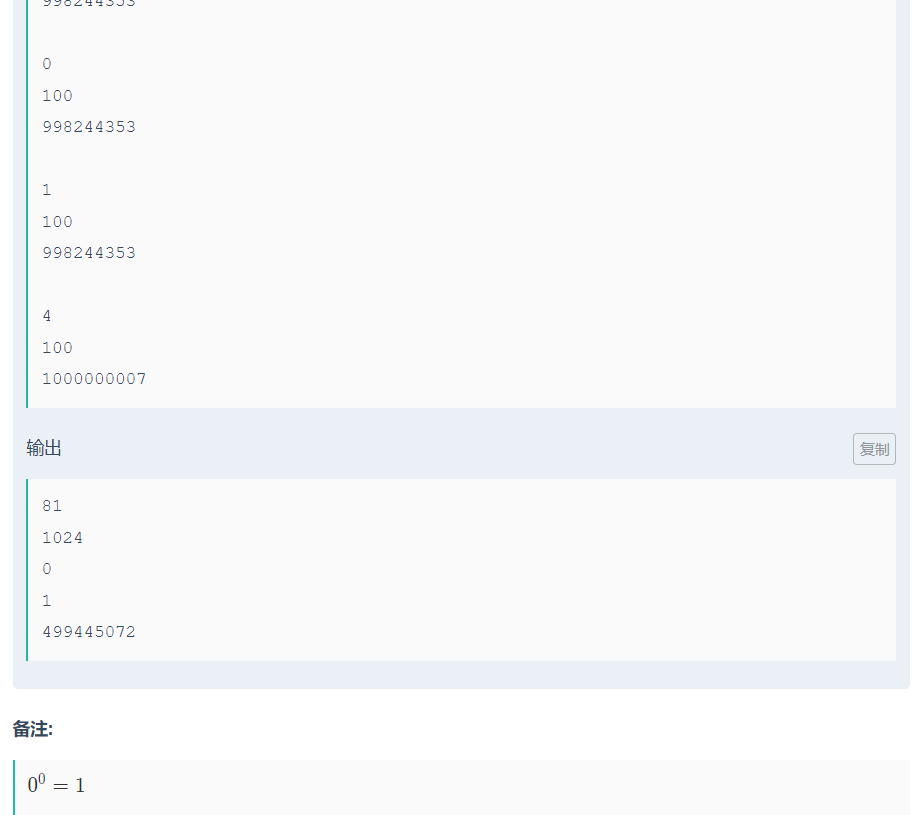
 对于b很大这种情况，请使用欧拉降幂

首先介绍一下欧拉函数（此处用到一些网络资料）

同余符号
含义
两个整数a，b，若它们除以整数m所得的余数相等，则称a，b对于模m同余
记作a≡b(mod m)
读作a同余于b模m，或读作a与b关于模m同余。
比如26≡14(mod 12)。

 

ll ol(ll n)
{
    int rea=n;
    for(int i=2;i*i<=n;i++)
    {
        if(n%i==0)
        {
            rea=rea-rea/i;
            while(n%i==0)
            n/=i;
        }
    }
    if(n>1)
      rea=rea-rea/n;
    return rea;
}
int main()
{
    ll a,b,c;
    cin>>a;
    cout<<ol(a)<<endl; 
} 

可得知该数范围内与这个数互质数的个数

欧拉降幂公式

 

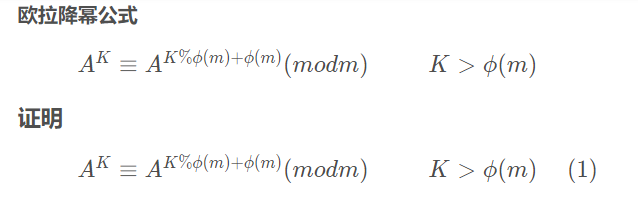
 由于我太弱这里不做证明

 

 上解题代码

 

#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<map>
#include<cmath>
typedef long long ll;
using namespace std;
bool note;
ll ol(ll n)
{
    ll rea=n;
    for(ll i=2;i*i<=n;i++)
    {
        if(n%i==0)
        {
            rea=rea*(i-1)/i;
            while(n%i==0)
            n/=i;
        }
    }
    if(n>1) rea=rea*(n-1)/n;
    return rea;
}
ll jc(string bb,ll mod)
{
    ll ans=0;
    for(ll i=0;i<bb.size();i++)
    {
        ans=ans*10+(bb[i]-'0');
        if(ans>=mod)
        {
            ans%=mod;note=1;
        }
    }
    return ans;
}
ll km(ll a,ll b,ll c)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=(res*a)%c;
        a=(a*a)%c;
        b>>=1;
    }
    return res;
}
int main()
{
    int sum;cin>>sum;
    while(sum--)
    {
       note=0;
       ll a,c;
       string b;
       cin>>a>>b>>c;
       ll cmod=ol(c);
       ll bb=jc(b,cmod);
       if(__gcd(a,c)!=1&&note) bb+=cmod;
       cout<<km(a,bb,c)<<endl;
    }
    return 0;
} 

等我啥时候懂了再来补降幂证明（