BUAA-OO-第一单元(表达式求导)总结
OO第一单元总结
一 . 程序的构建
1. 第一次作业
a.结构设计
第一次作业较为简单,由于可求导的式子限定为多项式,所以自己简单建立了单项式类和多项式类两个类。其中单项式类使用Biginteger存储指数和系数,实现了求导和toString方法,多项式类由Treemaps存储(系数,单项式)的键值对,并在构造器中过滤所有键为0的键值对,同样实现了求导和toString方法,具体的类图如下

b.性能的优化
- 重写
treeMap的sort方法(按系数从大到小排序,将第一项出现负号的单项式放在后面)eg:-1+2*x->2*x-1 x**2->x*x
c.程序结构及Metric分析
程序结构较为简单,而Metric分析结果不是很好(读取表达式时进行了相当复杂的特判),下面的表格给出了高于平均复杂度的方法的具体情况:
| Method | CogC(G) | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Expression.toString() | 10.0 | 2.0 | 7.0 | 8.0 |
| Power.toString() | 13.0 | 10.0 | 12.0 | 13.0 |
| Expression.Expression(String) | 36.0 | 1.0 | 28.0 | 28.0 |
| Average | 6.3 | 2.0 | 5.7 | 5.9 |
这里Expression的复杂性尤为突出,是由于自己在这里做了许多特判,对三个符号同时出现的情况直接暴力if else,缺少一个统一的规划。
下面给出每个类的代码行数统计(按行数倒序):
| Method | LOC | NLOD | RLOC |
|---|---|---|---|
| Expression.Expression(String) | 62.0 | 62.0 | 0.56 |
| Expression.toString() | 23.0 | 23.0 | 0.21 |
| Power.toString() | 23.0 | 23.0 | 0.43 |
| Power.derive() | 11.0 | 11.0 | 0.21 |
| Expression.derive() | 10.0 | 10.0 | 0.09 |
| PolyFactory.main(String[]) | 7.0 | 7.0 | 0.58 |
| Power.Power(BigInteger,BigInteger) | 5.0 | 5.0 | 0.09 |
| Expression.Expression(Map) | 3.0 | 3.0 | 0.02 |
| PolyFactory.PolyFactory(Map) | 3.0 | 3.0 | 0.25 |
| Power.getCoff() | 3.0 | 3.0 | 0.05 |
| Power.getPower() | 3.0 | 3.0 | 0.05 |
| Total | 153.0 | 153.0 | |
| Average | 13.91 | 13.91 | 0.21 |
2. 第二次作业
a.结构设计
这里自己已经考虑到了第三次作业可能出现的三角函数中出现嵌套的情况,所以按照指导书建立了二叉树,具体如下:

对于除BaseFactor之外的三个因子: SubFactor、 AddFactor 、MulFactor,均以factor类的实例作为左右节点,从而建立了以这三种因子为非叶子节点,以BaseFactor为叶子节点的二叉树。并在每个因子中实现了derive、toString方法,这种结构虽然能正确地求导,但优化起来实为困难(在优化中详述)。
而感觉这次作业另外一部分难点在于读取表达式生成表达式树,自己在不完全懂得递归下降的方法和不要求格式判断的情况下下选择了栈维护的表达式读取的方式,具体步骤如下:
前期准备:
1.建立存储因子的栈
2.建立存储计算符号的栈
3.为各种计算符号设置优先级(')'进行特判)
4.合并方法 : 符号栈pop出一个符号,因子栈pop出两个因子,根据符号确定运算关系合并两个因子,并将合并的结果压入因子栈中
读取表达式:
while(没读完) {
判断是否为因子,是则压入因子栈中,增加字符串指针, continue;
走到这已经是计算符号了)
-
为’)‘:一直
合并直到碰到右括号, pop右括号 -
其他:与符号栈顶的优先级进行比较,若大,则存入栈中,若小或相等,则进行
合并后再次比较
}
b.性能的优化
由于生成的表达式树难以化简(曾尝试设置去包装的方法降低树的深度,但由于太菜失败了),所以最后仅在toString方法中对 0, 常数进行了判断,并没有实现更进一步的优化。
c.程序结构及Metric分析
程序的结构较为清晰,但设置较不合理(如自己设置的Basefactor类中完全是空的,应该改为抽象类或者接口)缺少合理的接口类以进一步实现工厂模式和业务逻辑的分离。
而对于方法的复杂度分析,可以发现问题还在于读取字符串的部分,没有适宜地划分,导致出现长达58行的类方法,其实后来也发现bug全出在这些地方,下面的表格给出了高于平均复杂度的方法的具体情况:
| Method | CogC(G) | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| TrigF.derive() | 8.0 | 4.0 | 4.0 | 4.0 |
| DeriveFactory.methodProcess(String,Stack,Stack,int) | 12.0 | 1.0 | 13.0 | 13.0 |
| MulFactor.toString() | 15.0 | 7.0 | 8.0 | 16.0 |
| MulFactor.mergeMul(String,String) | 19.0 | 1.0 | 9.0 | 9.0 |
| DeriveFactory.read(String) | 23.0 | 3.0 | 13.0 | 13.0 |
| Average | 4.10 | 1.93 | 3.0 | 3.86 |
下面给出每个类的代码行数统计(按行数倒序):
| Method | LOC | NLOD | RLOC |
|---|---|---|---|
| DeriveFactory.read(String) | 48.0 | 48.0 | 0.37209302325581395 |
| MulFactor.mergeMul(String,String) | 48.0 | 48.0 | 0.32432432432432434 |
| MulFactor.toString() | 44.0 | 44.0 | 0.2972972972972973 |
| MulFactor.getString(String,String,String,String) | 32.0 | 32.0 | 0.21621621621621623 |
| AddFactor.toString() | 25.0 | 25.0 | 0.6097560975609756 |
| DeriveFactory.preProcess(String) | 25.0 | 25.0 | 0.1937984496124031 |
| SubFactor.toString() | 22.0 | 22.0 | 0.6111111111111112 |
| DeriveFactory.methodProcess(String,Stack,Stack,int) | 21.0 | 21.0 | 0.16279069767441862 |
| TrigF.derive() | 20.0 | 20.0 | 0.5263157894736842 |
| Power.toString() | 14.0 | 14.0 | 0.5384615384615384 |
| DeriveFactory.merge(Stack,Stack) | 12.0 | 12.0 | 0.09302325581395349 |
| TrigF.toString() | 10.0 | 10.0 | 0.2631578947368421 |
| Total | 394.0 | 394.0 | |
| Average | 13.586206896551724 | 13.586206896551724 | 0.1968031968031968 |
3. 第三次作业
a.结构设计
由于第二次作业构造的二叉表达式树难以进行化简,所以这里按照老师的提示设计了连加和连乘类,三角函数由于内部可以嵌套因子也进行了重构,总的类图如下

相对于第二次作业,这里减少了Basefactor这一形同虚设的类。
这次作业的另一个难点在于表达式的格式判定和读取。所以选择了递归下降的方法,在递归下降的过程中用栈维护表达式(栈的设置方法类似第二次作业)。而如果匹配失败,就throw异常并在main函数中输出WRONG FORMAT!(在这里自己对于sin中的项出现的不匹配情况由于忘了向外进一步throw Exception也出了bug)。
b.性能的优化
使用连加和连乘类本身可以很好地优化表达式(不准备实现拆括号级别的优化的情形下)(其实应该设计为TreeMap进行存储,并对equals方法重写为获得表达式的Hash值可能能更进一步实现合并同类项)。
c.程序结构及Metric分析
程序的结构与第二次结构差不多,由于实现了递归下降,将读取表达式的方法分散在各个子表达式的读取中,所以这部分代码的复杂度有了显著的下降,但ConMul中的toString方法和append方法中由于没有选择HashMap,导致在判断是否为同类项的步骤较为复杂,所以导致这部分代码的复杂度较高。下面的表格给出了高于平均复杂度的方法的具体情况:
| Method | CogC(G) | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| ConMul.append(Factor) | 9.0 | 1.0 | 5.0 | 5.0 |
| ExpFactory.itemCombine() | 11.0 | 1.0 | 6.0 | 7.0 |
| ExpFactory.isExp() | 14.0 | 2.0 | 8.0 | 10.0 |
| ConMul.toString() | 19.0 | 7.0 | 6.0 | 12.0 |
| Average | 3.51 | 1.81 | 2.62 | 3.24 |
下面给出每个类的代码行数统计(按行数倒序):
| Method | LOC | NLOD | RLOC |
|---|---|---|---|
| ConMul.toString() | 39.0 | 39.0 | 0.4482758620689655 |
| ExpFactory.itemCombine() | 32.0 | 32.0 | 0.1306122448979592 |
| ExpFactory.isExp() | 27.0 | 26.0 | 0.11020408163265306 |
| ExpFactory.readItem() | 26.0 | 26.0 | 0.10612244897959183 |
| ConAdd.toString() | 22.0 | 22.0 | 0.41509433962264153 |
| ConMul.append(Factor) | 22.0 | 22.0 | 0.25287356321839083 |
| ExpFactory.isTrig() | 22.0 | 22.0 | 0.08979591836734693 |
| Power.toString() | 19.0 | 19.0 | 0.5 |
| TrigF.toString() | 18.0 | 18.0 | 0.42857142857142855 |
| ExpFactory.inputMethod(String) | 16.0 | 16.0 | 0.0653061224489796 |
| ConMul.derive() | 15.0 | 15.0 | 0.1724137931034483 |
| ConAdd.append(Factor) | 14.0 | 14.0 | 0.2641509433962264 |
| ExpFactory.power() | 14.0 | 14.0 | 0.05714285714285714 |
| TrigF.derive() | 13.0 | 13.0 | 0.30952380952380953 |
| ExpFactory.readPower() | 12.0 | 12.0 | 0.04897959183673469 |
| ExpFactory.main(String[]) | 11.0 | 11.0 | 0.044897959183673466 |
| ExpFactory.getAr() | 10.0 | 10.0 | 0.04081632653061224 |
| ExpFactory.readLeft() | 10.0 | 10.0 | 0.04081632653061224 |
| ExpFactory.readRight() | 10.0 | 10.0 | 0.04081632653061224 |
| ExpFactory.getDigit() | 9.0 | 9.0 | 0.036734693877551024 |
| Power.derive() | 9.0 | 9.0 | 0.23684210526315788 |
| ExpFactory.isExpF() | 8.0 | 8.0 | 0.0326530612244898 |
| ConAdd.derive() | 7.0 | 7.0 | 0.1320754716981132 |
| ExpFactory.init() | 7.0 | 7.0 | 0.02857142857142857 |
| ConMul.ConMul() | 6.0 | 6.0 | 0.06896551724137931 |
| ConAdd.ConAdd() | 5.0 | 5.0 | 0.09433962264150944 |
| ExpFactory.readSpace() | 5.0 | 5.0 | 0.02040816326530612 |
| TrigF.TrigF(boolean,Factor,BigInteger) | 5.0 | 5.0 | 0.11904761904761904 |
| Cons.toString() | 4.0 | 4.0 | 0.3076923076923077 |
| ExpFactory.rank(Character,Character) | 4.0 | 4.0 | 0.0163265306122449 |
| Cons.Cons(BigInteger) | 3.0 | 3.0 | 0.23076923076923078 |
| Cons.derive() | 3.0 | 3.0 | 0.23076923076923078 |
| ExpFactory.isEnd() | 3.0 | 3.0 | 0.012244897959183673 |
| ExpFactory.isFactor() | 3.0 | 3.0 | 0.012244897959183673 |
| Factor.derive() | 3.0 | 3.0 | 0.6 |
| Power.Power(BigInteger) | 3.0 | 3.0 | 0.07894736842105263 |
| Power.getPower() | 3.0 | 3.0 | 0.07894736842105263 |
| Total | 442.0 | 441.0 | |
| Average | 11.945945945945946 | 11.91891891891892 | 0.0835222978080121 |
二三次作业类的耦合度分析
(由于第一次作业较为简单,就不加入分析了)。
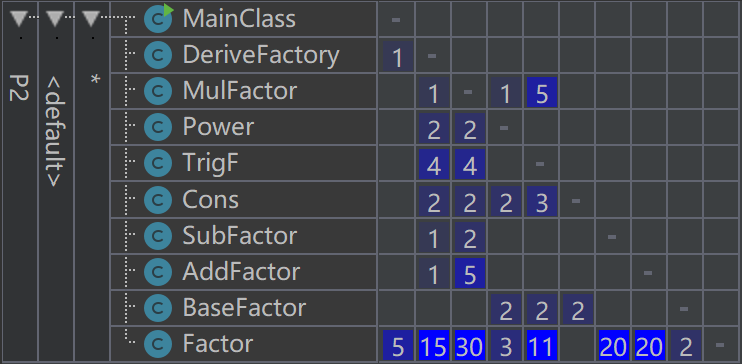
P2 依赖关系矩阵(DSM)(类似图的矩阵表示,节点的度数越大,耦合程度越高)
P3 依赖关系矩阵(DSM)
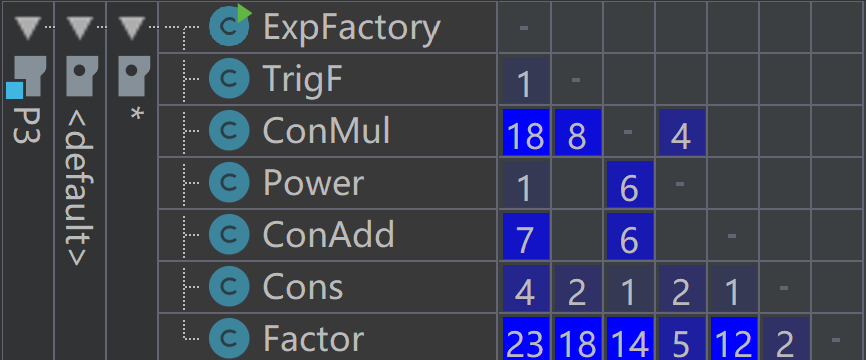
这里我们可以看到矩阵的非零元集中在下三角区域,意味着这种调用关系式是自顶向下的,而上三角部分出现了非零元素意味着较不该出现的两个类相互间的调用的存在。在这里我们看到,第三次作业相比第二次作业的优点在于减少了类的数目的情形下同时减少了总的类之间的耦合度。但第三次作业相对第二次作业也有一定的缺陷在于,ExpFactory作为工厂类,几乎与其他所有的类都有较高程度的耦合(P3的矩阵的第一列元素较大),这是不应该出现的,如需优化,应该在ExpFactory中设计与Factor类的抽象接口,并将调用相关类的部分集中在一个方法中而非分散在多个子方法中(其实这也是工厂类的基本要求),仅与Factor进行耦合而非与多个节点类进行耦合。这样才能做到解耦并提高程序的可扩展性。
二. 程序的bug
第一次作业
第一次作业较为简单,但由于自己对题目对表达式的递归定义没有了解透彻,对于三个连续的+-号出现时有不正确的处理。
第二次作业
第二次作业出现了较多的bug(导致自己连互测都没进, 现罗列如下:
-
读取表达式时,由于对优先级的理解不到位,导致栈top的计算符优先级较高时,在进行合并后直接将后面的计算符push进了栈中而没有重新判断此时栈顶的运算符优先级的高低。
-
优化时,由于优化过程中通过判断toString方法返回的子字符串有无±号来判断是否需要括号,但忘了考虑特殊情况,导致有些必须需要括号的地方删去了括号。
-
在对输入的初始处理时,忘了将"(+"转化为"(",导致在后面将这个+当做了一个运算符,进而导致出错。
第三次作业
第三次作业由于使用了递归下降的方法,没有出现上面那样稀奇古怪的错误(早点用递归下降就好了),但在强测中出现了一个bug:
由于自己的异常的throw理解不到位,导致在读取sin和cos中的表达式因子时,即使格式出错,也在递归层中的catch中被处理了而没有向最外层抛出,没有被最外层程序捕捉,从而没有被判定为格式错误。
三. bug的发现及解决
1.自己的bug
-
构造特殊的临界数据, 如" ", "1", "x",处于表达式定义的临界边缘处的数据(如"1---1*x")
-
构造较高嵌套程度的表达式,这样可以导致表达式被我们定义的结构高度包装,导致最后树具有较高的高度,可以判断出一下容易导致stackoverflow或rte的问题。这里就是这样测出了自己第二次作业出现的一个问题,类似fib的递归计算在计算较大数时重复递归子树,我构造的toString方法与之类似地重复调用了多次子树,导致最后超出运行时间。自己最后选择记忆的策略以避免重复递归调用
大致如下:@Override public String toString() { if (!this.expression.equals("null")) { return expression; } String left = this.left.toString(); String right = this.right.toString(); if (left.matches("[+-]?\\d+") && right.matches("[+-]?\\d+")) { expression = new BigInteger(left).subtract(new BigInteger(right)).toString(); return expression;这样就保证了toString方法经过一次调用就作为这个节点类的一个属性存储下来,在次被调用时将之间输出,避免指数复杂度的toStirng方法,从而顺利解决了问题
2.互测hack策略
自己没有构造自动测评的机器(太菜太懒),只使用python实现了简单的将8个人的程序批量打包并运行,根据我的手工输入给出结果的简单脚本。在第一次作业中,我主要通过阅读别人代码去寻找bug,并记得自己手工测试了几个三个符号同时出现的情况没有问题时,通过阅读其中一个同学的代码发现其三个符号的正确判断时由漏洞的,并找到了这一特殊情况并成功hack。第三次作业中,通过读同学的代码发现他们对于空白符的判断时,如果使用正则表达式的\s,则会出现不只匹配空格和制表符,还会匹配其他许多空白符的情形。也有同学对于空串的处理不正确,当然由于互测规则的更改,最后没有成功hack(但是也算找到了他人的问题)。
四. 重构经历总结
自己是每次作业都进行了完全的重构。第一次基本是面向过程的方法,用HashMap基本完成了任务。第二次重构基本按照要求构造了二叉表达式树,构造过程比较顺利。但在优化时遇到了巨大的困难,于是在这里又进行了一次重构改用HashMap存储一个因子的常数系数、幂函数指数、三角函数指数,并类似第一次作业进行求导计算,但最后还是交上了表达式树的版本并在toString方法中暴力串匹配以合并同类项;第三次作业本来可以建立在第二次作业的基础上而不需要重构的,但由于在toString方法中合并同类项的方法bug问题过多,所以选择了重构,并改用连加和连乘类。并在表达式的读取使用了递归下降的方法。
这里对于自己二三次作业架构的对比有更多的认识,希望在这里拿出来分享下(血的教训啊~)
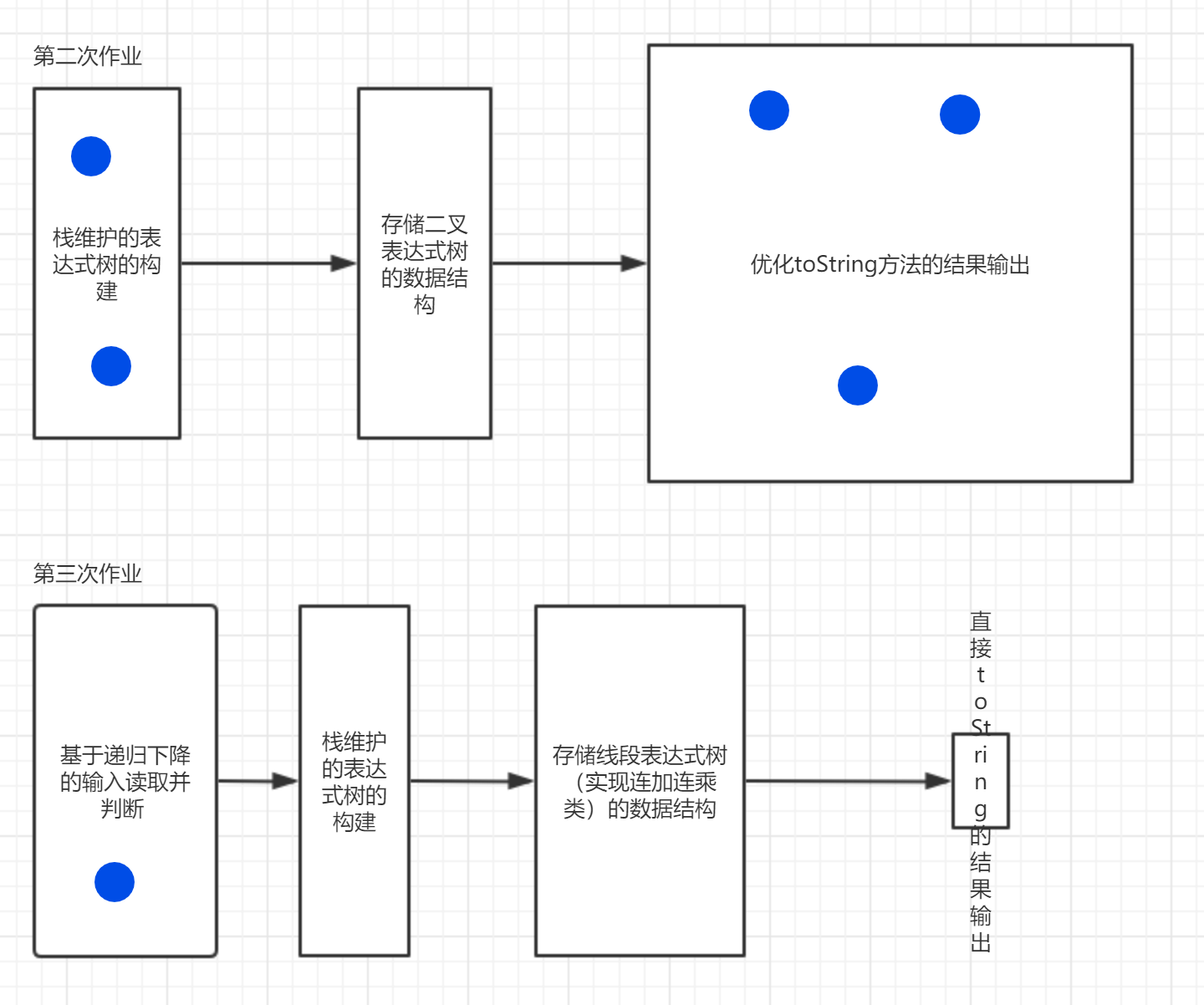
(这张图的下半部分不是画的有问题,我是故意的~)上面这张图是我的二三次作业的输入->处理->输出 的程序结构,而上述每个部分的大小正比于我实际构造过程中花费的时间,而蓝色的点表示在这里出现了bug(一个蓝点算一个修复的同质bug)。(bug们表示:看你这一步挺"大"的,就搁你这安家8 o(╥﹏╥)o)。这里对于两个图的变化做一个简单的说明:
1.由于第三次作业中实用递归下降读取表达式串,所以栈维护的树的构建无需考虑过多,只需考虑节点和运算符什么时候push pop即可。故降低了这部分的复杂度。
2.由于连加连乘类的构建,使得toString无需任何优化,就可以达到比较好的化简效果(不算那些优化到能提取公因式的巨佬~),大大降低了这部分花费的时间。也使得出错的地方变少。
教训总结:
1.用好数据结构,合适的数据结构往往能事半功倍。2.如果发现自己写某个步骤花的时间过长,考虑的问题过多还是考虑重构吧,不要硬挺。
五. 心得体会
初次接触面向对象的编程,感觉虽然被虐的很惨但是还是有挺多的收获的,下面谈一谈自己感触最深的几点吧:
1. 如果具有较好的面向对象的思想,理清各个类之间的关系,复杂的程序不一定意味着‘复杂’的实现代码
这里拿出代码复杂度的图的占比来看:

从左到右依次是第一次作业、第二次作业、第三次作业的CogC(G)(Metric 中对代码复杂度的一种度量),而这种逐渐变得均衡化的原因,在于面向对象的设计思想在三次作业中是逐步提升的。此时,纵然代码本身实现的程序逐步变得更加复杂,最复杂的方法的复杂度却在下降,可以说,面向对象的思想使得我的程序更加的“均衡”,而第三次作业中出现的bug,也由于功能较为独立的方法间的分离,不仅使得bug减少,也使得发现并解决bug也变的更加容易。
2. 复杂度高的代码更容易出现bug,也更难找到出现bug的原因
个人统计了自己出现的bug的地方,发现"恰巧"全部都出现在复杂度最高的方法之中,不是在其中漏写了一部分特判,就是在if块中好几个或条件中的逻辑有漏洞甚至有错误。另一方面, 在debug的时候(可能是我自己太没耐心了。)de几行还可以,当行数一多而且跳来跳去时,自己就变得不耐烦了。这里也不应该陷入另一个误区,即代码的分散不等同于功能的分散,自己在第二次作业中,读取表达式的部分过长导致会扣性能分,于是自己就好无厘头地将其分成几个函数。结果debug 的时候在不同函数间跳来跳去让找bug变得更加困难。相反地,在第三次作业的表达式读取中,由于通过递归下降的方式,将不同的因子的读取分离开来。使得自己在解决强测出的bug(还是不要出bug更好。。。)时很快便定位到bug 的根源并在添加一行代码后成功解决了bug(具体见三.bug的发现及解决)。总而言之,将功能根据实际情况进行划分并分散到不同的方法中,不仅能让我们出更少的bug,也能在找到bug后更快地定位原因并解决。
3. 阅读别人的代码可以有很大的收益(当然需要在一个好的互测屋)
之前自己是抱着找bug的心态去阅读别人的代码的,但当真正打开别人的优秀的代码去阅读时,是能够学到很多东西的。比如,在第一次作业中,了解到 (?<tag> ...)可以用于正则表达式匹配时设置组的名称防止混乱并增加代码可读性;在第三次作业中,见到巨佬的代码可以对于过度包装的因子(树具有很高的高度但实际上没必要有这么高)进行化简,从而从根源上对树的结构进行优化。另一方面,也许在学习别人的代码时,抱着寻找bug的心态去看,会让我们更加细致地阅读,并加入自己的逻辑思考去寻找可能存在的漏洞(可能会有更好的学习效果?)。
4. 有时候测评机找不到的问题,也许可以通过一行一行读代码解决
这里的测评机找不到不是测评机没测出来,而是没给测试的stdin。。。(别误解了~
记得上学期计组有一道思考题是关于逻辑验证和样例验证之间的关系的。由于我们的程序根本不可能覆盖所有的样例去进行测试,所以逻辑验证是很重要的。这里在能力有限的情况下其实可以将逻辑验证看做一行一行去读代码,这种bug可能是逻辑产生的漏洞,或者忘记了对某一特殊情况进行处理,甚至是正则表达式的模式串本身有误。当然,这样去寻找bug较为适用于程序基本正确,测评机构造的样例基本通过的前提之下。这种本来就大概率找不到自己的错误的方式也是比较考验人的耐心的。也许这也印证了荣老师说的"能测出的bug那都不叫bug"了吧。

