可逆矩阵定理
设矩阵A为n*n矩阵，那么以下命题等价：
1.A是可逆矩阵。
2.存在n*n矩阵C使得CA=I。
3.存在n*n矩阵D使得AD=I。
4.A的各列线性无关。
5.对于向量空间R^n中任意向量b，方程AX=b有且仅有一个解。
6.A的各列张成R^n。
7.A行等价于单位矩阵。
8.方程AX=0仅有平凡解。
9.A.T是可逆矩阵。
10.A有n个主元位置，有n个主元列，没有自由元。
向量空间方面：
10.矩阵的零空间nul A只含有零向量，即{0}。
11.矩阵的各列构成R^n的一组基。
12.矩阵的列空间col A=R^n
13.矩阵列空间的维度dim col A=n
14.矩阵的秩rank A=n
15.矩阵零空间的维度dim nul A=0
接下来我们要一点一点地完成论证，透过纷繁芜杂的信息，抽丝剥茧地思考矩阵可逆的本质；并体会方阵与非方阵，非奇异矩阵和奇异矩阵的异同。
根据可逆矩阵的定义：
因此，1蕴含2，1蕴含3.
接下来证明2蕴含8，即命题“存在n*n矩阵C使得CA=I”蕴含“方程AX=0仅有平凡解。”
由题可得：CAX=C（AX）=C*0=0
CAX=（CA）X=IX=0
可得X=0.
8蕴含10，即“方程AX=0仅有平凡解”蕴含“A有n个主元位置，有n个主元列，没有自由元。”：
（接上）这同时说明AX=0没有自由变量（有自由变量的话就有无穷多解），它的每个变量都是主元（有n个主元位置），每列都是主元列。
10蕴含7，即“A有n个主元位置，有n个主元列，没有自由元。”蕴含“A行等价于单位矩阵”：
已知A是方阵且有n个主元位置，则主元必然位于主对角线上（n个主元位置在不同的行）。所以A的行最简形是单位矩阵In。
7蕴含1，即“A行等价于单位矩阵”蕴含“A是可逆矩阵。”
我们先证明：
另外，有：
因此：
这也正是我们求逆矩阵的方法：作增广矩阵（A|E），经过行变换得（E|A^-1）.
至此，我们完成了以下几个命题的等价证明：
1==> 2==> 8==> 10==> 7==> 1
3蕴含5，即“存在n*n矩阵D使得AD=I。”蕴含“对于向量空间R^n中任意向量b，方程AX=b有且仅有一个解。”：
ADb=Ib=b
得A（Db）=b
所以向量x=Db满足Ax=b。
命题5和6完全等价。参见向量组的线性相关性。
5蕴含1，即“对于向量空间R^n中任意向量b，方程AX=b有且仅有一个解。”蕴含“A是可逆矩阵。”
由题得A在每一行都有一个主元位置，又因为A是方阵，主元位于主对角线上，A行等价与单位矩阵，故A是可逆矩阵。
我们完成了以下几个命题的等价证明：
1==>3==>5==>1
命题4和8是完全等价的。参见向量组的线性相关性。
1蕴含9，即“A是可逆矩阵”蕴含“A.T是可逆矩阵”：
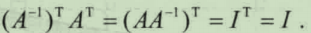
因为A.T.T=A，故将A于A.T互换后可得9蕴含1.
至此，完成了可逆矩阵定理1-10的证明。
接下来我们考虑这个问题：假设一个m*n矩阵A，若存在n*m矩阵C和D使CA=I，AD=I；我们可以说矩阵A是可逆的吗？
事实上，我们可以推出A是方阵（即m=n）且C=D。所以A是可逆的。我们说只有方阵才有可逆的概念。
但是，只满足一个条件的话不能推出A 可逆。
接下来我们开始论证。
1.设CA=In（n*n单位矩阵），A是m*n矩阵，C是n*m矩阵。先证明Ax=0只有平凡解：
CAX=C（AX）=C*0=0
CAX=（CA）X=IX=0
可得X=0.
因此得到A的各列线性无关。所以列向量的个数小于等于列向量的维度。即行数大于等于列数。
2.设AD=Im（m*m单位矩阵），A是n*m矩阵，D是m*n矩阵。先证明对于R^m中的向量b，Ax=b有解：
ADb=Ib=b
得A（Db）=b
所以向量x=Db满足Ax=b。
因此A的各列张成Rm，列向量个数大于等于列向量维度，即行数小于等于列数。
结合1，2可得行数等于列数，所以A是方阵。
C=D非常容易论证：
