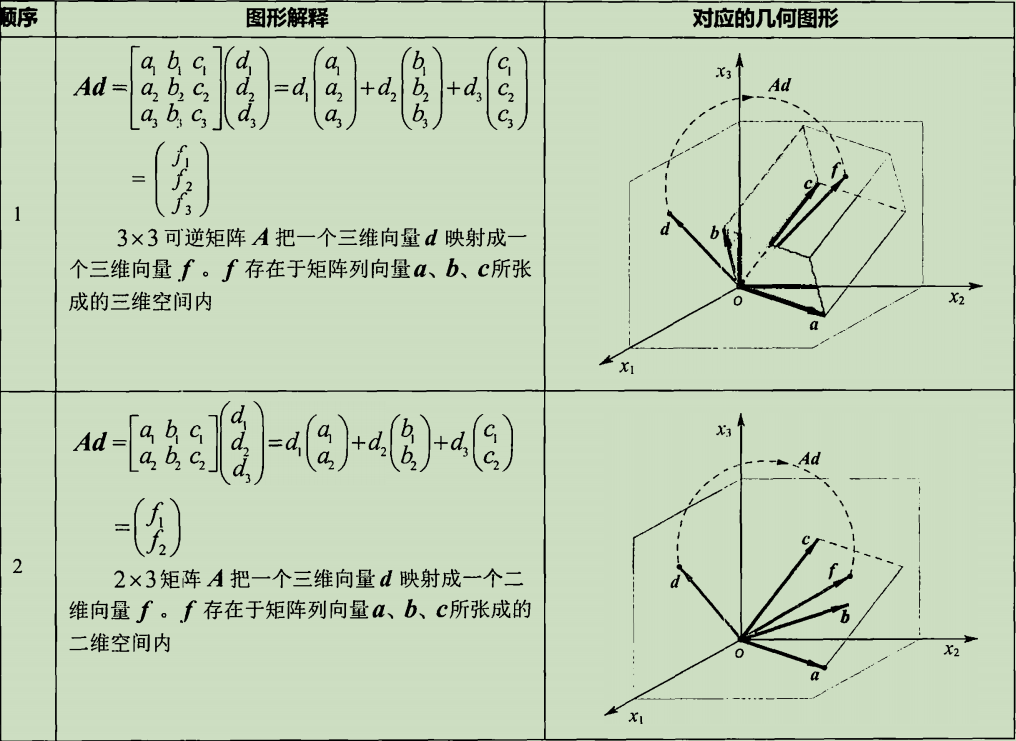
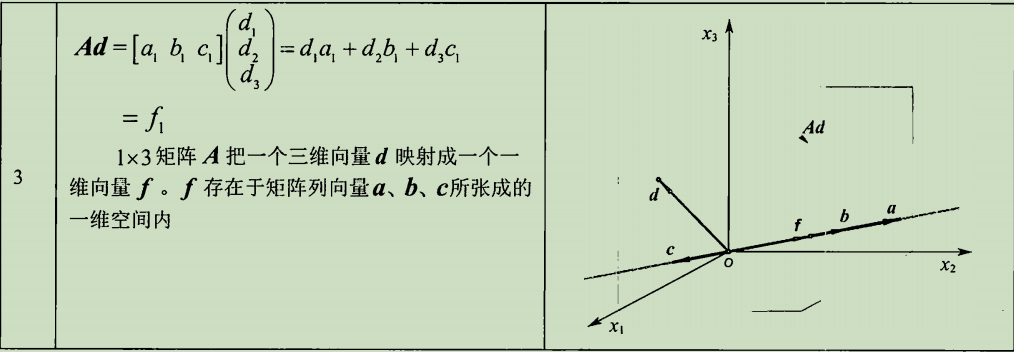
矩阵与变换
向量组的线性相关性
题一:

a:是。它们都是线性无关的。含有两个向量的向量组,若两个向量的分量对应成比例则线性相关,否则线性无关。
b:否。两两线性无关并不能说明总体线性无关。
c:否。有可能某一或某些向量并不是其他向量的线性组合,但整体依然线性相关。
d:是。因为向量个数超过了向量的元素个数(维度)。也就是说它构成的系数矩阵是欠秩的,也必然有自由变量。
向量组线性相关性的定义:

我对线性无关的理解是:找不到这样一组不全为零(非平凡)的权值,使得向量组中有至少一个向量能被其他向量的线性组合所表示。
反之,只要向量组里有一个向量能被其他向量线性表示,我们就称这个向量组线性相关。
而且,如果向量组线性相关,必然有无穷多组权使得向量方程有解。
——>齐次方程有无穷多非零解。
如果我们能找到一组值(x1,x2,x3……xn)将这n向量分别进行放缩后,能够首尾相接,那我们就说它们是线性相关的。
以二维向量组为例,已知,两个不共线的二维向量可以表示平面所有向量,它们构成的向量集合span(r1,r2)=R^2,那么向量数量超过两个的二维向量组必然线性相关。
因为剩余的向量都包含在构造的向量集里了。
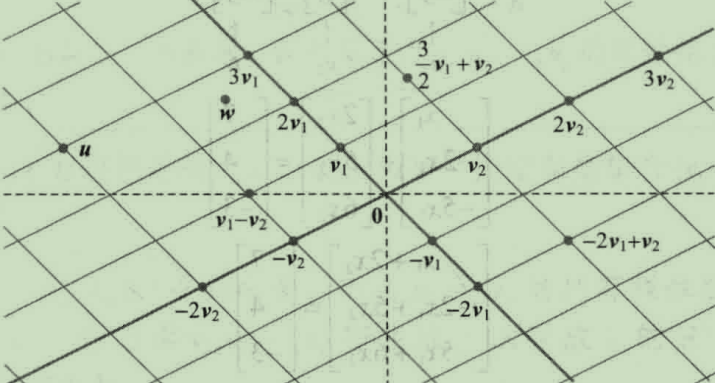
v1,v2的所有线性组合,等于二维空间的所有向量
线性组合或表示式的代数意义是向量数乘和加法的综合。它的几何意义,就是对向量组内的向量长度进行缩放后,依照平行四边形法则进行合并相加。
两个向量组等价的几何意义也很好理解:它们所扩张的直线,平面,空间(所有线性组合的集合)重合。
如何判断向量组是否线性相关?有以下几个方法:
1.向量组的向量个数超过向量的元素个数(维数)时,该向量组必然线性相关。
2.研究向量组构成的齐次线性方程组的解的情况,如果有非平凡解,则线性相关,否则线性无关。
非平凡解<——>矩阵的秩小于列数n<——>无穷多解<——>有自由变量<——>线性相关
只有零解<——>矩阵的秩等于列数n<——>有唯一解<——>线性无关
(矩阵的秩的定义为:行或列向量的极大线性无关组,小于等于(行数或列数的最小值)。行秩等于列秩等于秩。
矩阵的秩不可能大于列数,例如两个三维向量不可能张成三维空间。)
推论——>计算该向量组构成的行列式,如果|A|=0,则线性相关。
对于R^n中的向量x,R^m中的向量T(x) 称为x在T作用下的像。所有像的集合称之为值域。
(R^n称为定义域,R^m称为余定义域。)
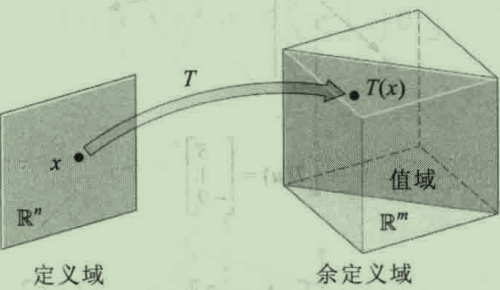
矩阵就是变换。
从R^n到R^m的所有线性变换T,都是矩阵变换x——>Ax。T的值域就是A所有列向量的所有线性组合。
说了半天,什么叫做线性变换?
1)叠加性:和的变换等于变换的和。f(x1+x2)=f(x1)+f(x2)
2)齐次性:比例的变换等于变换的比例。f(kx)=kf(x)
这两点合起来,就是线性组合:f(k1x1+k2x2)=k1f(x1)+k2f(x2)。每个矩阵变换都是线性变换。
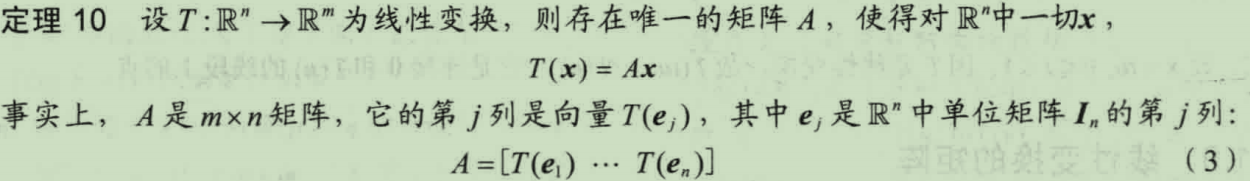
我们把这样的矩阵称为线性变换T的标准矩阵。
满射与单射

满射
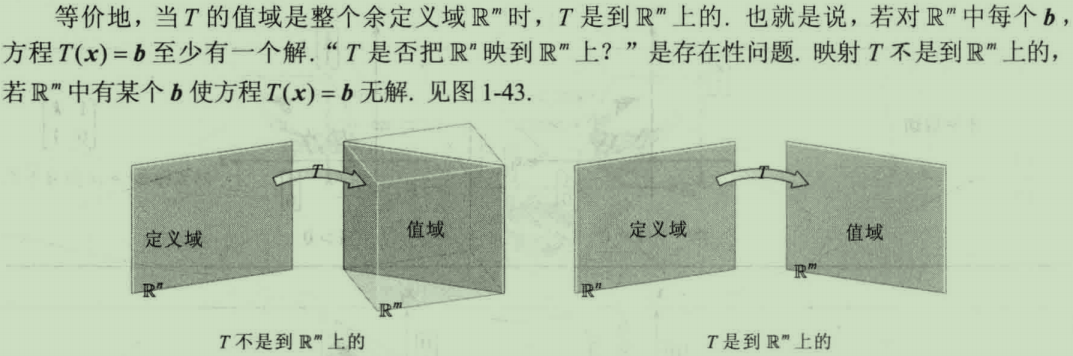
如果矩阵的列向量构造的线性组合集=R^m,即R(A)行满秩时,我们说这个映射是满射的。
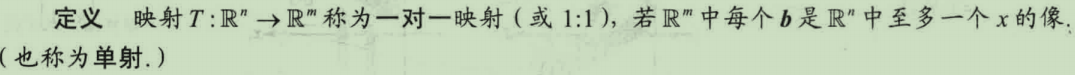
单射(一对一映射翻译不恰当)
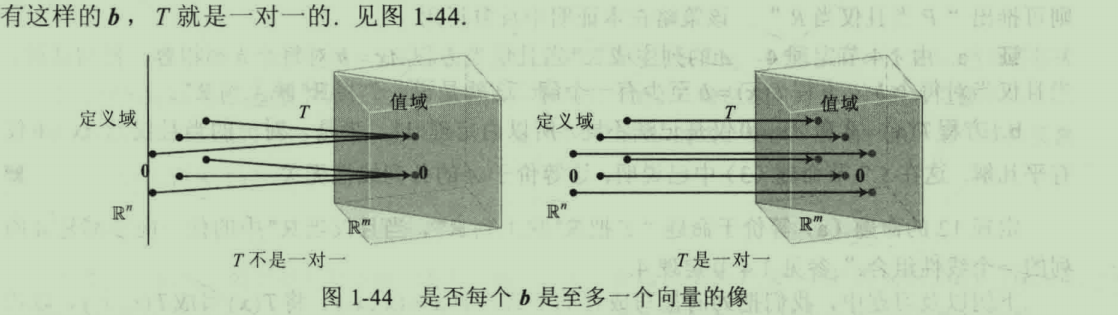

题目二:

解:R(A)=3,说明矩阵的列向量张成R^3,若x为四维向量,则AX=b有解。故(1)对。
方程AX=b有一个自由变量,意味着对于每一个b,有多个X与之对应,所以该映射不是单射。
(R(A)<4,意味着有一个维度在变换中被消解了。我们得到的是投影。)
矩阵与向量的乘法
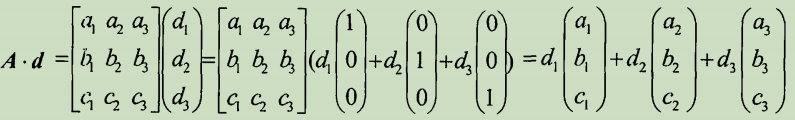
矩阵与向量相乘
矩阵与向量相乘,就是把向量映射到矩阵A的列向量所张成的空间(集合)里。新向量就是以原向量各个元素为权(坐标)的列向量(坐标基)的线性组合。
我们知道向量是既有大小有有方向的量,它的存在和描述是不依赖于坐标系的,它表示的是两点之间的位移。(一个点离开坐标系是没法描述的。)
向量经矩阵转换后,得到的是它在矩阵的列向量构成的空间中的投影。