Elgamal加密算法和数字签名
简述:ElGamal公钥密码体制是由 T.ElGamal于 1985年提出的,直到现在仍然是一个安全性能良好的公钥密码体制。该算法既能用于数据加密也能用于数字签名,其安全性依赖于计算有限域上离散对数这一难题。下面详细介绍该算法。
1.背景
ElGamal公钥密码体制是由 T.ElGamal于 1985年提出的,与 Diffie-Hellman密钥分配体制密切相关。ElGamal密码体系应用于一些技术标准中,如数字签名标准(DSS)和 S/MIME电子邮件标准。直到现在仍然是一个安全性能良好的公钥密码体制。该算法既能用于数据加密也能用于数字签名,其安全性依赖于计算有限域上离散对数这一难题。Elgamal加密方案可以视为DHKE协议的拓展,无容置疑,其安全性也是基于离散函数问题和Diffie_Hellman问题的难度。
在对称密钥加解密,在他们进行任何加密之前,双方必须要拥有一个秘密的key。一直以来,密钥的分发一直存在很多问题,因为密钥分配涉及到面对面的见面,可信中介的使用,或者是通过一个加密的渠道发送key。通过加密渠道发送key取决于这个加密渠道的安全性。Diffie-Hellman密钥交换方案提供了实际中密钥分配问题的解决方案,即它允许双方通过不安全的信道进行交流,得到一个共同密钥。该实验使用python3.8实现了Elgamal加密算法和数字签名。
2.主要算法
2.1
Diffie-Hellman密钥交换算法
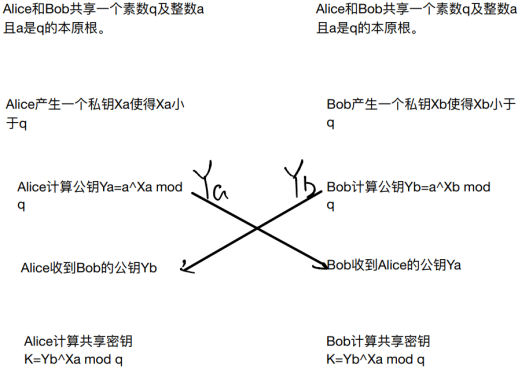
图一.DH密钥交换算法流程图
1.Alice和Bob交换了各自公钥后,计算出公共密钥(DH算法),就可以用同一个密钥进行加密和解密。
2.Diffie-Hellman密钥交换的安全性建立在下述事实之上:求关于素数的模素数幂运算相对容易,而计算离散对数却非常困难;对于大素数,求离散对数被认为是不可行的。
3.例:输入一个质数,作为Alice和Bob的公钥:7
取原根为: 3
Alice随机产生的私钥: 3
A计算出的公钥YA,传递给B: 6
Bob随机产生的私钥: 1
B计算出的公钥YB,传递给A: 3
A获取的共享密钥: 6
B获取的共享密钥: 6
2.2
Elgamal加密的基本原理
该加密算法可以分为以下几个步骤:
1.选取一个大素数q和q的一个原根a。
2.Alice将选取一个私钥Xa,计算Ya=a^Xa mod q.{q,a,Ya}将作为公钥传递给Bob
3.Bob获取公钥后,选取自己的私钥Xb,计算:
K=Ya^Xb mod q,
C1=a^Xb mod q.
K是双方的公共密钥,用来加解密明文M。密文C2=M*K mod q.
C1传递给Alice,是获取K的媒介。
1.Alice获取Bob的密文(C1,C2)后,开始解密。
K=C1^Xa mod q
M=C2*K-1 mod q
解密完成。
2.3
在有限域Zq中求取指定元素乘法逆元。
欧几里得算法用于求取整数a,b的最大公因数gcd(a,b),基于gcd(a,b)=gcd(b,a mod b)成立。拓展的欧几里得算法用于求取a*x+b*y=gcd(a,b)的整数解(x,y)。
实验代码:
def extendgcd(a,b): #返回一个集合:(x,y,d)满足ax+by=d
if b == 0:
return (1,0,a)
else:
(x,y,d)=extendgcd(b,a%b)
x,y=y,(x-(a//b)*y)#x-(a//b)*y即为x mod y
return (x,y,d)
当算法进行到最后一步,即a=d,b=0时,必然有(x,y)=(1,0)满足a*1+b*0=d。此即为回溯的起始点。
考察回溯过程中上下两层的关系。有:
a * x1 + b * y1 = gcd(a,b)
b * x2 + (a%b) * y2 = gcd(b,a%b)
# d= gcd(a,b) = gcd(b,a%b) 算法中每一步返回值都满足d=ax+by
得:a * x1 + b * y1 = b * x2 + (a%b) * y2
其中a%b换为a-(a/b)*b。
得:a * x1 + b * y1 = b * x2 + (a - (a / b) * b) * y2
=b * (x2 - (a / b) * y2) + a * y2
=a * y2 + b * (x2 - (a / b) * y2)
得到:
X1=y2, y1=(x2 - (a / b) * y2)
得到方程b * x2 + (a%b) * y2 = g(b,a%b) 的解x2, y2,就能得到方程a * x1 + b * y1 = g(a,b) 的解x1,y1。
在Elgamal算法中,拓展欧几里得算法用于求取密钥K的关于模φ(n)的逆元K0。
即令
K*K0 mod q=1,求K0。
令
K*x+q*y=gcd(K,q)=1#K与q互质
该式正是拓展欧几里得算法公式。求取x。
等式两边同时模q,得K*x mod φ(n)=1。
即x就是我们要求的K模q的逆元K0。
2.4Elgamal数字签名的基本原理
1.生成密钥
同ElGamal 加密方案一样,ElGamal 数字签名方案的基本元素是素数q和α,其中α是q的原根。用户Alice选取私钥Xa,1<Xa<q-1。计算Ya=a^Xa mod q,公钥为{q, a, Ya}
2.签名与验证
数字签名的步骤:
1.Alice选取随机密钥K,K满足1<K<q-1,且gcd(K,q-1)=1。
2.计算r=a^K mod q.
3.计算K-1 mod q-1.
4.计算s=(m-Xa*r)*K-1 mod q-1.
5.返回签名(r,s)
签名验证步骤:
Bob现在收到了Alice的消息m,公钥(q, a, Ya)和签名(r,s)。
1.计算V1=a^m mod q.
2.计算V2=(Ya^r)*(S1^S2) mod q.
若V1=V2,说明该签名合法,消息确是Alice所发。
3.算法实现
点击查看代码
'''
实现环境:python 3.8
使用库: random
'''
#3.1加密算法实现:
import random as rd
def sushu(num):#判断素数
judge=1
for x in range(2,num):
if num%x==0:
judge=0
return False
if judge==1:
return True
def getsushu():#生成大质数
while True:
x=rd.randint(50000,100000)
if sushu(x)==True:
return x
def fun0(a,b):#辗转相除法
if a%b==0:
return b
else:
return fun0(b,a%b)
def extendgcd(a,b):#返回一个集合:(x,y,d)满足ax+by=d
if b == 0:
return (1,0,a)
else:
(x,y,d)=extendgcd(b,a%b)
x,y=y,(x-(a//b)*y)#x-(a//b)*y即为x mod y
return (x,y,d)
def Ord(n):#求原根
result=[]
for x in range(1,n):
if pow(x,n-1,n)==1:
result.append(x)
for i in range(1,n-1):
if pow(x,i,n)==1:
result.remove(x)
break
if len(result)!=0:
return result
def get_KPB(q,a):
XA=rd.randint(2,q-2)
YA=pow(a,XA,q)
return {'q':q,'a':a,'YA':YA},XA
def encrypt(text,KAB):
k=rd.randint(2,KAB['q'])
K=pow(KAB['YA'],k,KAB['q'])#一次性密钥,用完即毁
C1=pow(KAB['a'],k,KAB['q'])
C2=pow(K*text,1,KAB['q'])
return [C1,C2]
def decrypt(miwen,XA,q):
C1=miwen[0]
C2=miwen[1]
K=pow(C1,XA,q)
K0=extendgcd(K,q)[0] if extendgcd(K,q)[0]>0 else extendgcd(K,q)[0]+q
M=pow(C2*K0,1,q)
return M
def change0(text):#字符串转utf-8
return list(map(ord,text))
def change1(alist):#utf-8转字符串
result = ''
for x in alist:
result += chr(x)
return result
if __name__ == '__main__':
q=getsushu()
print('随机生成的素数为:',q)
a=Ord(q)[0]
print('选取的本原根为:',a)
KAB,XA=get_KPB(q,a)
print('生成的公钥为:',KAB)
text=input('输入待加密明文:')
temp=change0(text)
mlist=[]
for x in temp:
miwen=encrypt(x,KAB)
mlist.append(miwen)
print('密文列表:',mlist)
wlist=[]
for x in mlist:
wlist.append(decrypt(x,XA,q))
print('解密后明文:',change1(wlist))
#3.2数字签名实现:
import elgamal加密 as el
import random as rd
def get_KPB(q,a):
XA=rd.randint(2,q-2)
print('XA(d)=',XA)
YA=pow(a,XA,q)
return {'q':q,'a':a,'YA':YA},XA
#q,a,YA是公钥,XA是私钥
def sig(text,KAB,XA):
ke=0
while True:
k = rd.randint(2,KAB['q']- 2)
if el.fun0(k,(KAB['q']-1))==1:
ke=k
break
r=pow(KAB['a'],ke,KAB['q'])
ke0 = el.extendgcd(ke,KAB['q']-1)[0] if el.extendgcd(ke,KAB['q']-1)[0]>0 else el.extendgcd(ke,KAB['q']-1)[0] +(KAB['q']-1)
s=pow((text-XA*r)*ke0,1,(KAB['q']-1))
return [r,s]
def ver(text,sign,KAB):
r=sign[0]
s=sign[1]
t=pow((KAB['YA']**r)*(r**s),1,KAB['q'])
print('对每一段签名进行验证:t=',t,end='')
print('; a**m mod q=',pow(KAB['a'],text,KAB['q']))
if t==pow(KAB['a'],text,KAB['q']):
return True
else:
return False
if __name__ == '__main__':
print('该程序实现Elgamal数字签名:')
q=el.getsushu()
print('选取的大素数q为:',q)
a=el.Ord(q)[0]
print('选取的本原根a为:',a)
KAB,XA=get_KPB(q,a)
print('公钥为:',KAB)
text=input('输入待签名原文:')
text=el.change0(text)
print('将原文转为utf8编码:',text)
sign=[]#签名列表
for x in text:
sign.append(sig(x, KAB, XA))
print('签名为:',sign)
answer=False
for x in sign:
answer=ver(text[sign.index(x)],x,KAB)
print(answer)
3.1Elgamal加密算法测试
随机生成的素数为: 68993
选取的本原根为: 3
生成的公钥为: {'q': 68993, 'a': 3, 'YA': 8845}
输入待加密明文:nuistisouruniversity
密文列表: [[16888, 18105], [35921, 23717], [6908, 23122], [36150, 54825], [56786, 53807], [30866, 53053], [41182, 20569], [21660, 13487], [58789, 58315], [27149, 59733], [64748, 66959], [7238, 20154], [52728, 38058], [16732, 870], [41589, 7571], [30510, 39857], [35682, 6061], [44380, 53045], [26560, 7106], [6173, 39758]]
解密后明文: nuistisouruniversity

3.2Elgamal数字签名测试
该程序实现Elgamal数字签名:
选取的大素数q为: 71129
选取的本原根a为: 3
XA(d)= 69878
公钥为: {'q': 71129, 'a': 3, 'YA': 39879}
输入待签名原文:nuistisouruniversity
将原文转为utf8编码: [110, 117, 105, 115, 116, 105, 115, 111, 117, 114, 117, 110, 105, 118, 101, 114, 115, 105, 116, 121]
签名为: [[56796, 68014], [8258, 2747], [60548, 36193], [16302, 23267], [57639, 12898], [6678, 12877], [38448, 33657], [23709, 23941], [3104, 61397], [16734, 62], [70552, 25995], [53287, 11700], [48957, 30813], [57255, 56036], [10789, 44621], [45145, 21420], [16890, 4095], [11339, 6305], [45804, 56644], [26456, 11289]]
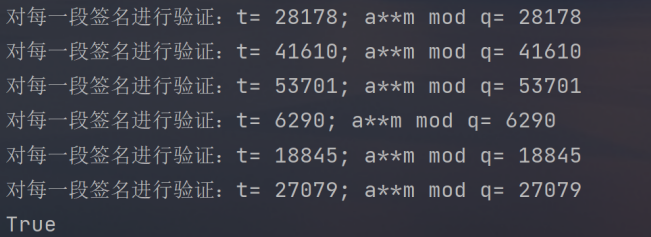
对每一段签名进行验证:t= 34761; a**m mod q= 34761
对每一段签名进行验证:t= 56535; a**m mod q= 56535
对每一段签名进行验证:t= 6290; a**m mod q= 6290
对每一段签名进行验证:t= 53701; a**m mod q= 53701
对每一段签名进行验证:t= 18845; a**m mod q= 18845
对每一段签名进行验证:t= 6290; a**m mod q= 6290
对每一段签名进行验证:t= 53701; a**m mod q= 53701
对每一段签名进行验证:t= 33154; a**m mod q= 33154
对每一段签名进行验证:t= 56535; a**m mod q= 56535
对每一段签名进行验证:t= 41610; a**m mod q= 41610
对每一段签名进行验证:t= 56535; a**m mod q= 56535
对每一段签名进行验证:t= 34761; a**m mod q= 34761
对每一段签名进行验证:t= 6290; a**m mod q= 6290
对每一段签名进行验证:t= 27347; a**m mod q= 27347
对每一段签名进行验证:t= 28178; a**m mod q= 28178
对每一段签名进行验证:t= 41610; a**m mod q= 41610
对每一段签名进行验证:t= 53701; a**m mod q= 53701
对每一段签名进行验证:t= 6290; a**m mod q= 6290
对每一段签名进行验证:t= 18845; a**m mod q= 18845
对每一段签名进行验证:t= 27079; a**m mod q= 27079
True

4.总结
Elgamal公钥密码体制既能用于数据加密也能用于数字签名。其中的区别在于:信息发送方可以用公钥加密,接收方用自己的私钥解密。信息发送方用自己的私钥为消息签名,接收方则用公钥进行验证。
ElGamal加密算法产生的密文长度是明文的两倍。使得通信的信息量增大。同时Elgamal加密算法一个最大的特点是在加密过程中进行随机方式的加密方法,这种方法有着很好的抗攻击性。
待改进的地方还有很多,比如素数随机产生的算法,求原根的算法等。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号