拓展欧几里得算法

密码学最基础的算法。

点击查看代码

def extendgcd(a,b):#返回一个集合：(x,y,d)满足ax+by=d
    if b == 0:
        return (1,0,a)
    else:
        (x,y,d)=extendgcd(b,a%b)
        x,y=y,(x-(a//b)*y)
        return (x,y,d)
print(extendgcd(12,36))
print(extendgcd(56,3))
print(extendgcd(4589,393))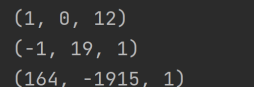

解析：

欧几里得算法：

gcd(a,b)=gcd(b,a mod b)

用递归实现：

不断进行模运算，直到b=0时，a即为最大公因数。

该算法用于求a,b的最大公因数d。对其进行拓展可用于求ax+by=gcd(a,b)的整数解(x,y)。

当算法进行到最后一步，即a=d，b=0时，必然有(x,y)=(1,0)满足a*1+b*0=d。此即为回溯的起始点。

考察回溯过程中上下两层的关系。有：

a * x1 + b * y1 = gcd(a,b)
b * x2 + (a%b) * y2 = gcd(b,a%b)   

# d= gcd(a,b) = gcd(b,a%b) 算法中每一步返回值都满足d=ax+by

 

得：a * x1 + b * y1 = b * x2 + (a%b) * y2

其中a%b换为a-(a/b)*b。
得：a * x1 + b * y1 = b * x2 + (a - (a / b) * b) * y2

                =b * (x2 - (a / b) * y2) + a * y2

                  =a * y2 + b * (x2 - (a / b) * y2)

得到：

X1=y2, y1=(x2 - (a / b) * y2)

得到方程b * x2 + (a%b) * y2 = g(b,a%b) 的解x2, y2，就能得到方程a * x1 + b * y1 = g(a,b) 的解x1,y1。