BZOJ1766 Photo
题目
平面上有若干个点,现在要求用最少的底边在X轴上且面积小等A的矩形覆盖所有点,这些矩形可以重叠。 N<=100,A<=2000000
思路
一开始想的是简单的区间dp。
\(f[l,r]\)表示覆盖完\([l,r]\)一段区间的所有点的最小矩形数,然后很快就发现了不对之处:
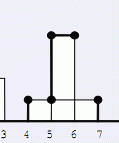
对于图中所示情况,单纯考虑区间之间的分割是行不通的,也就是说,对于相互重叠的矩形,高度那一维也很有必要记录。
重新定义状态:\(f[i][j][k]\)当\([i,j]\)区间,高度\(>k\)的点被覆盖的最优情况。
接下来考虑从上往下转移:
对于当前区间\([l,r,h]\),一种方式直接递归转移\([l+1,r,h]+1\)
另外一种方式,直接考虑从\(l\)开始,覆盖一定程度的点到\(j\),计算出最大能够达到的高度\(mxh\)
那么在\(mxh\)之上的点可以递归处理,式子为\(f[l][j][mxh]+f[j+1][r][h]+1\)。
代码
#include<bits/stdc++.h>
using namespace std;
void tomin(int &x,int y){if(x>y)x=y;}
void tomax(int &x,int y){if(x<y)x=y;}
struct node{
int x,y;
bool operator < (const node& res)const{
if(x!=res.x)return x<res.x;
return y>res.y;
}
}A[105];
int n,S,f[105][105][105],mx[105][105],B[105],bc;
int mp[200005];
int dfs(int l,int r,int h){
if(mx[l][r]<=h)return 0;
if(l==r)return f[l][r][h]=1;
if(~f[l][r][h])return f[l][r][h];
int L=l,R=r;
while(L<=R&&A[L].y<=h)L++;
while(L<=R&&A[R].y<=h)R--;
int &res=f[l][r][h];res=dfs(L+1,R,h)+1;
for(int i=L+1;i<=R;i++){
int d=A[i].x-A[L].x;
int mxh=mp[S/d];
if(mxh<=h)break;
tomin(res,dfs(L,i,mxh)+dfs(i+1,R,h)+1);
}
return res;
}
int main(){
memset(f,-1,sizeof(f));
scanf("%d%d",&n,&S);
for(int i=1;i<=n;i++)
scanf("%d%d",&A[i].x,&A[i].y),B[++bc]=A[i].y;
sort(A+1,A+n+1);
int len=1;
for(int i=2;i<=n;i++)
if(A[i].x!=A[i-1].x)A[++len]=A[i];
n=len;sort(B+1,B+bc+1);bc=unique(B+1,B+bc+1)-B-1;
for(int i=1;i<=bc;i++)mp[B[i]]=i;
for(int i=1;i<=n;i++)
A[i].y=lower_bound(B+1,B+bc+1,A[i].y)-B;
for(int i=1;i<=200000;i++)
if(!mp[i])mp[i]=mp[i-1];
for(int i=1;i<=n;i++)
for(int j=i,res=A[i].y;j<=n;j++)
tomax(res,A[j].y),mx[i][j]=res;
printf("%d\n",dfs(1,n,0));
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号