题解 [BJOI2019]勘破神机
Description
Solution
\(m=2\)
设填满宽度为 \(n\) 的核心的方案数为 \(f(n)\) , 那么答案即为 \(\sum\limits_{i=l}^r\binom{f(i)}{k}\) .
考虑求出 \(f(n)\) 的通项 .
不难发现最后两行只有两种可能的情况
1.

2.

两种情况的答案分别是 \(f(n-1),f(n-2)\),
那么就得到了递推式 \(f(n)=f(n-1)+f(n-2)\).
记 \(f(x)\) 为 \(f\) 数列的生成函数 .
那么有
\(f(x)=xf(x)+x^2f(x)+1\)
\(\displaystyle f(x)=\frac{1}{1-x-x^2}\)
将分母因式分解
\(\displaystyle(1-x-x^2)=-(x-x_1)(x-x_2),x_1=\frac{-1+\sqrt5}2,x_2=\frac{-1-\sqrt5}2\)
\(\displaystyle f(x)=\frac{-1}{(x-x_1)(x-x_2)}\)
尝试将分母拆开
\(\displaystyle f(x)=\frac{a}{x-x_1}+\frac{b}{x-x_2}\)
需要构造 \(a,b\) 满足
\(a(x-x_2)+b(x-x_1)=-1\)
解得
\(\begin{cases}a=-\frac{\sqrt5}{5}\\b=\frac{\sqrt5}{5}\end{cases}\)
\(\begin{aligned}f(x)&=\frac{a}{x-x_1}+\frac{b}{x-x_2}\\&=\frac{a}{x_1}\frac{1}{\frac{x}{x_1}-1}+\frac{b}{x_2}\frac{1}{\frac{x}{x_2}-1}\\&=-(\frac{a}{x_1}\frac{1}{1-\frac{x}{x_1}}+\frac{b}{x_2}\frac{1}{1-\frac{x}{x_2}})\\&=-(\frac{a}{x_1}\sum\limits_i(\frac{x}{x_1})^i+\frac{b}{x_2}\sum\limits_i(\frac{x}{x_2})^i)\end{aligned}\)
那么
\(\displaystyle[x^n]f(x)=-(\frac{a}{x_1}(\frac{1}{x_1})^n+\frac{b}{x_2}(\frac{1}{x_2})^n)\)
代入 \(x_1,x_2,a,b\), 得
\(\displaystyle[x^n]f(x)=\frac{\sqrt5}{5}(\frac{1+\sqrt5}{2})^{n+1}-\frac{\sqrt5}{5}(\frac{1-\sqrt5}{2})^{n+1}\)
为了方便将 \(f\) 整体平移一下 , 计算答案时将 \(l,r\) 也平移即可 .
\(\displaystyle[x^n]f(x)=\frac{\sqrt5}{5}(\frac{1+\sqrt5}{2})^n-\frac{\sqrt5}{5}(\frac{1-\sqrt5}{2})^n\)
记 \(\displaystyle A=\frac{\sqrt5}{5},B=-\frac{\sqrt5}{5},X=\frac{1+\sqrt5}{2},Y=\frac{1-\sqrt5}{2}\)
则 \(\displaystyle[x^n]f(x)=AX^n+BY^n\)
然后对答案式进行变形
\(\begin{aligned}&\sum\limits_{n=l}^r\binom{f(n)}{k}\\&=\sum\limits_{n=l}^r\frac{f(n)^{\underline k}}{k!}\\&=\frac{1}{k!}\sum\limits_{n=l}^r\sum\limits_{i=0}^k(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}(AX^n+BY^n)^i\\&=\frac{1}{k!}\sum\limits_{n=l}^r\sum\limits_{i=0}^k(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}\sum\limits_{j=0}^i\binom ij(AX^n)^j(BY^n)^{i-j}\\&=\frac{1}{k!}\sum\limits_{i=0}^k(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}\sum\limits_{j=0}^i\binom ijA^jB^{i-j}\sum\limits_{n=l}^r(X^n)^j(Y^n)^{i-j}\end{aligned}\)
前面两个求和符号可以 \(O(k^2)\) 枚举 , 最后一个求和符号为等比数列求和 .
\(\sqrt5\) 可以通过把数域拓展为 \(a+b\sqrt5\) 来处理 .
注意特判公比为 \(1\)
\(m=3\)
与 \(m=2\) 类似 , 先考虑求出通项 .
不难发现只有长度为偶数时才有解 , 那么设 \(g(n)\) 为填满宽度为 \(2n\) 的核心的方案数 .
最后的放置方案有三类
1.
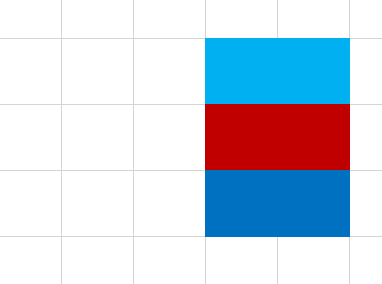
2.
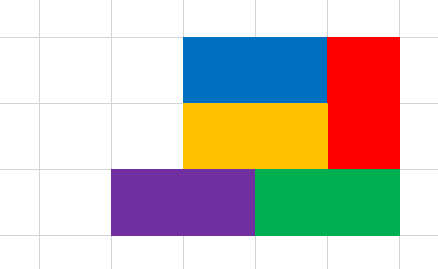
注意到这种填充可以无限延伸 , 即这种也被分到该类中
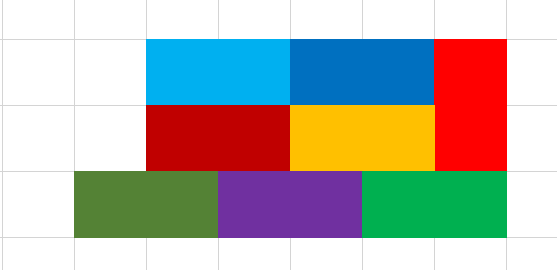
3. 为 2 的镜像
这三种的方案数分别为 \(g(n-1),\sum\limits_{i<n}g(i),\sum\limits_{i<n}g(i)\)
那么得出递推式 \(g(n)=g(n-1)+2\sum\limits_{i<n}g(i)\)
写成生成函数就是
\(g(x)=xg(x)+2\sum\limits_{i=1}x^ig(x)+1\)
\(\displaystyle g(x)=xg(x)+\frac{2x}{1-x}g(x)+1\)
\(\displaystyle g(x)=\frac{1-x}{x^2-4x+1}\)
使用和 \(m=2\) 时完全相同的技术可以得到通项
\(\displaystyle[x^n]g(x)=\frac{3-\sqrt3}{6}(2-\sqrt3)^n+\frac{3+\sqrt3}{6}(2+\sqrt3)^n\)
使用和 \(m=2\) 时完全相同的技术可以 \(O(k^2)\) 求出答案 .
Code
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
template<typename T=int>T read()
{
T ret=0;bool f=0;char c=getchar();
while(c>'9'||c<'0')f|=(c=='-'),c=getchar();
while(c>='0'&&c<='9')ret=(ret<<3)+(ret<<1)+(c^48),c=getchar();
return f?-ret:ret;
}
int T,m;
const int mod=998244353;
const int maxn=550;
namespace global
{
int qpow(int a,int b){int ret=1;for(;b;b>>=1,a=(ll)a*a%mod)if(b&1)ret=(ll)ret*a%mod;return ret;}
struct modint
{
int val;
int qmod(int x)const{return x>=mod?x-mod:x<0?x+mod:x;}
modint(ll v=0){val=v%mod;}
modint operator +(const modint&x)const{return qmod(val+x.val);}
modint operator -(const modint&x)const{return qmod(val-x.val);}
modint operator *(const modint&x)const{return (ll)val*x.val%mod;}
modint operator /(const modint&x)const{return (ll)val*qpow(x.val,mod-2)%mod;}
};
modint fac[maxn],inv[maxn],s[maxn][maxn];
void prework()
{
int n=510;
fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i;
inv[0]=inv[1]=1;for(int i=2;i<=n;i++)inv[i]=inv[mod%i]*(mod-mod/i);
for(int i=2;i<=n;i++)inv[i]=inv[i-1]*inv[i];
s[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)s[i][j]=s[i-1][j-1]+s[i-1][j]*(i-1);
}
modint C(int n,int m){return fac[n]*inv[m]*inv[n-m];}
}using global::C,global::prework,global::modint,global::s,global::inv;
namespace sub1
{
struct Int
{
modint a,b;
Int(modint aa=0,modint bb=0){a=aa;b=bb;}
Int operator +(const Int &x)const{return {a+x.a,b+x.b};}
Int operator -(const Int &x)const{return {a-x.a,b-x.b};}
Int operator *(const Int &x)const{return {a*x.a+b*x.b*5,a*x.b+b*x.a};}
Int operator *(const modint &x)const{return {a*x.val,b*x.val};}
Int operator /(const Int &x)const{modint bas=x.a*x.a-x.b*x.b*5;return {(a*x.a-b*x.b*5)/bas,(b*x.a-a*x.b)/bas};}
};
Int qpow(Int a,ll b){Int ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
const Int A(0,598946612),B(0,399297741),X(499122177,499122177),Y(499122177,499122176);
int calc(ll l,ll r,int k)
{
int ret=0;
for(int i=0;i<=k;i++)
{
Int sum(0,0);
for(int j=0;j<=i;j++)
{
Int sum1(0,0);
Int now=qpow(X,j)*qpow(Y,i-j);
if(now.a.val==1&&now.b.val==0)sum1=Int(r-l+1,0);
else sum1=(qpow(now,r+2)-qpow(now,l+1))/(now-(Int){1,0});
sum=sum+sum1*C(i,j)*qpow(A,j)*qpow(B,i-j);
}
if((k-i)&1)ret=(ret-(ll)sum.a.val*s[k][i].val%mod+mod)%mod;
else ret=(ret+(ll)sum.a.val*s[k][i].val%mod)%mod;
}
return (ll)ret*inv[k].val%mod*global::qpow((r-l+1)%mod,mod-2)%mod;
}
}
namespace sub2
{
struct Int
{
modint a,b;
Int(modint aa=0,modint bb=0){a=aa;b=bb;}
Int operator +(const Int &x)const{return {a+x.a,b+x.b};}
Int operator -(const Int &x)const{return {a-x.a,b-x.b};}
Int operator *(const Int &x)const{return {a*x.a+b*x.b*3,a*x.b+b*x.a};}
Int operator *(const modint &x)const{return {a*x.val,b*x.val};}
Int operator /(const Int &x)const{modint bas=x.a*x.a-x.b*x.b*3;return {(a*x.a-b*x.b*3)/bas,(b*x.a-a*x.b)/bas};}
};
Int qpow(Int a,ll b){Int ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
const Int A(499122177,831870294),B(499122177,166374059),X(2,998244352),Y(2,1);
int calc(ll l,ll r,int k)
{
int len=(r-l+1)%mod;
r=r/2;l=(l-1)/2+1;
int ret=0;
for(int i=0;i<=k;i++)
{
Int sum(0,0);
for(int j=0;j<=i;j++)
{
Int sum1(0,0);
Int now=qpow(X,j)*qpow(Y,i-j);
if(now.a.val==1&&now.b.val==0)sum1=Int(r-l+1,0);
else sum1=(qpow(now,r+1)-qpow(now,l))/(now-(Int){1,0});
sum=sum+sum1*C(i,j)*qpow(A,j)*qpow(B,i-j);
}
if((k-i)&1)ret=(ret-(ll)sum.a.val*s[k][i].val%mod+mod)%mod;
else ret=(ret+(ll)sum.a.val*s[k][i].val%mod)%mod;
}
return (ll)ret*inv[k].val%mod*global::qpow(len,mod-2)%mod;
}
}
int main()
{
T=read();m=read();
prework();
while(T--)
{
ll l=read<ll>(),r=read<ll>();int k=read();
if(m==2)printf("%d\n",sub1::calc(l,r,k));
else printf("%d\n",sub2::calc(l,r,k));
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号