URAL1031——DP——Railway Tickets

Description

The railway line “Yekaterinburg-Sverdlovsk” with several stations has been built. This railway line can be represented as a line segment, railway stations being points on it. The railway line starts at the station “Yekaterinburg” and finishes at the station “Sverdlovsk”, so stations are numbered starting from “Yekaterinburg” (it has number 1) and “Sverdlovsk” is the last station.

Cost of the ticket between any two stations depends only on a distance between them. The prices for the tickets are specified in the following table.

distance X between stations	price for the ticket
0 < X ≤ L1	C1
L1 < X ≤ L2	C2
L2 < X ≤ L3	C3

Direct tickets from one station to another can be booked if and only if the distance between these station does not exceed L₃. So sometimes it is necessary to book several tickets to pay for the parts of the whole way between stations.

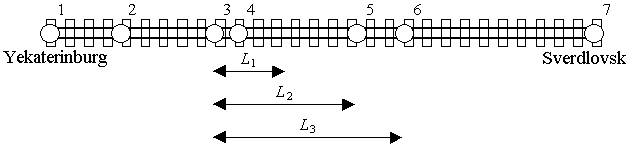
For example, on the railway line shown at the figure above there are seven stations. The direct ticket from the second station to the sixth one can not be booked. There are several ways to pay for the travel between these stations. One of them is to book two tickets: one ticket at price C₂ to travel between the second and the third stations, and other at price C₃ to travel between the third and the sixth stations. Note, that though the distance between the second and the sixth stations is equal to 2 L₂, the whole travel can not be paid by booking two tickets at price C₂, because each ticket is valid for only one travel and each travel should start and end only at stations.

Your task is to write a program, that will find the minimal cost of the travel between two given stations.

Input

The first line of the input contains 6 integers L₁, L₂, L₃, C₁, C₂, C₃ (1 ≤ L₁ < L₂ < L₃ ≤ 10 ⁹, 1 ≤ C₁ < C₂ < C₃ ≤ 10 ⁹) in the specified order with one space between. The second line contains the amount of stations N (2 ≤ N ≤ 10000). The third line contains two different integers separated by space. They represent serial numbers of stations, the travel between which must be paid. Next N−1 lines contain distances from the first station (“Yekaterinburg”) on the railway line to others. These distances are given as different positive integers and are arranged in the ascending order. The distance from “Yekaterinburg” to “Sverdlovsk” does not exceed 10 ⁹. The distance between any neighboring stations does not exceed L₃. The minimal travel cost between two given stations will not exceed 10 ⁹.

Output

Program should print to the output the only number, which is the minimal travel cost between two given stations.

Sample Input

input	output
3 6 8 20 30 40 7 2 6 3 7 8 13 15 23	70

 大意：先输入距离区间以及价格区间 

n表示有n个车站  ，我们要从s1出发到达s2，接下来n-1行表示的是除第一个车站外每个车站距离第一个车站的距离，问你从s1到s2最少所需要的花费

定义 dp[i] 表示当前位于第i个车站已经用去的钱

状态转移方程  dp[i] = min(dp[i],dp[j]+C[j]，所以要写一个表达式来求出j的范围，还是太弱了orz，写不出来

原文题解

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int dp[10010];
int L[4],C[4],s[10010];
const int inf = 0x3f3f3f3f;
int main()
{
    int s1,s2;
    int n;
    while(~scanf("%d%d%d%d%d%d",&L[1],&L[2],&L[3],&C[1],&C[2],&C[3])){
        scanf("%d",&n);
        scanf("%d%d",&s1,&s2);
        if(s1 > s2) {
            int temp = s1;
            s1 = s2;
            s2 = temp;
        }
        s[1] = 0;
        for(int i = 2; i <= n ;i++)
            scanf("%d",&s[i]);
        for(int i = 1; i <= n;i++)
            dp[i] = inf;
        dp[s1] = 0;
        for(int k = s1 + 1; k <= s2; k++){
            for(int p = 1; p <= 3; p++){
                int j = k - 1;
                while(j >= s1){
                    if(s[k] - s[j] > L[p])
                        break;
                    dp[k] = min(dp[k],dp[j]+C[p]);
                    j--;
                }
            }
        }
        printf("%d\n",dp[s2]);
    }
    return 0;
}