分智慧果 - 2021算法与数据结构实验题
算法与数据结构实验题 8.19 分智慧果
题目内容
★实验任务
老师准备把一筐智慧果分给班上的同学，第i个同学(从1开始编号)分到 \(a_i\) 个智慧果。Bonez (编号为1)是个自私的人，如果他的智慧果数不是班上最多的（即存在某位同学的智慧果数大于他的智慧果数），他会悄悄把别的同学的智慧果放进自己的那堆里。请问他至少需要从其他同学那里拿多少个智慧果，才可以使自己的智慧果数是班上最多的？
★数据输入
第一行为正整数n; 第二行为n个正整数a[1..n]。\((0 \le a_i \le 10^5)\)
60%的数据 \(1 \le n \le 100\).
100%的数据 \(1 \le n\le 100000\)
★数据输出
输出最少需要从别处拿的智慧果数。
输入示例
3
1 8 0
输出示例
4
题目分析
\(n_1 : n_i \in U, \forall\ n_1 \ge n_i\) 换句话说, 就是要让 Bonez 的智慧果数量不少于任何一个同学.
这里我们给出一个例子.
若要让 Bonez 的智慧果数量最多, 那么遵循贪心的原则, 每一次我们都让智慧果数量最多的同学给 Bonez 一个智慧果.
这样看还是不太直观, 我们不妨按照智慧果数量排个序.
要使得 Bonez 的智慧果最多且操作次数最少, 我们则需要每次从智慧果最多的人那里拿出一个给 Bonez, 并且在该操作之后动态地维护智慧果序列. 直到 Bonez 成为智慧果数量最多的人. 操作的次数就是题目要求的答案.
在这个例子中, 我们不难看出, 算法的关键就是在于怎样每一次都可以快速的找到序列中最多智慧果的数量. 如何实现呢? 当然是优先队列.
算法实现
在这个例子当中, 我们需要高效的知道当前序列中最多的智慧果数量是多少. 而优先队列正好可以满足我们的这个要求.
优先队列可以实现 O(1) 的查找最值. 若算上维护的操作, 那么一次查询和分配智慧果就是 O(1 + nlog n) = O(nlog n).
对于具体的优先队列实现这里就不再赘述.
为查找序列中的最大值, 本题使用的是大根堆, 并且以数组存储近似满二叉堆的形式存储堆.
给出近似满二叉堆的相关接口, 后续堆的操作有用到.
int _Parent(int x) { return ((x - 1) >> 1); }
int _LChild(int x) { return ((x << 1) + 1); }
int _RChild(int x) { return ((x << 1) + 2); }
题目中主要用到的操作只有两个分别是: 插入 和 修改
insert()
我们没办法直接知道待插入元素在堆中的正确位置, 所以我们要通过这种间接的方式先插入再维护, 从而完成一次堆插入操作.
1/ 插入新元素至堆底
将新插入的元素插入到堆的最底层, 即数组的最后一个位置, 使其成为一片新的叶子.
2/ 调整元素位置, 保持堆的结构
然后再沿着新插入的这个节点, 向根回溯. 每一次回溯都去判断当前节点及其两个子节点是否满足大根堆的结构.
若否, 则更新堆, 交换不符合的两个节点的位置, 使得在这个子堆中仍然保持着堆的结构.
不断回溯, 直到到达堆的根. 完成一次插入操作.
void insert(int n)
{
// 1. 插入新元素至堆底
_heap[_size++] = n;
// 2. 调整元素位置, 保持堆的结构
int buf, scan = _size - 1; // scan 从堆底开始扫描; buf 是 scan 的父节点用来判断堆结构是否正确
while ((buf = _Parent(scan)) >= 0) // 循环, 直到 scan 的父节点非零的时候退出
{
if (_heap[scan] < _heap[buf]) // 堆结构已经正确, 退出循环.
break;
swap(_heap[scan], _heap[buf]); // 交换节点, 使其满足堆的结构
scan = buf; // 更新 scan, 以继续向根节点迭代检查.
}
}
建树的过程就是不断地往优先队列中加入新的元素. 还是用上面提到的例子来演示, 如动图所示.
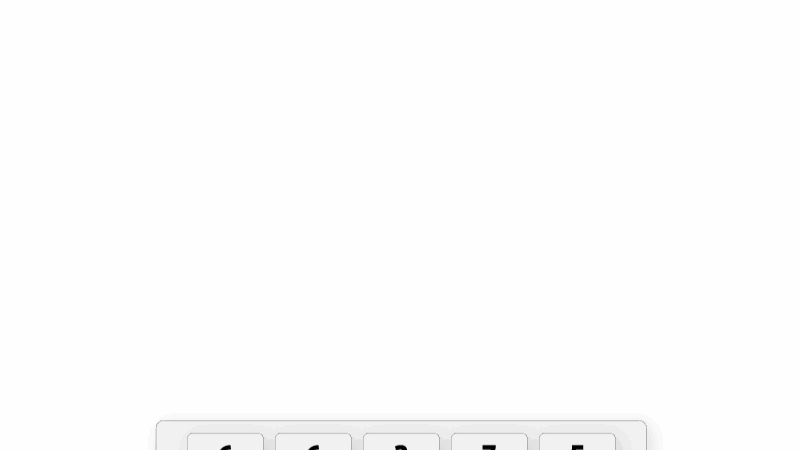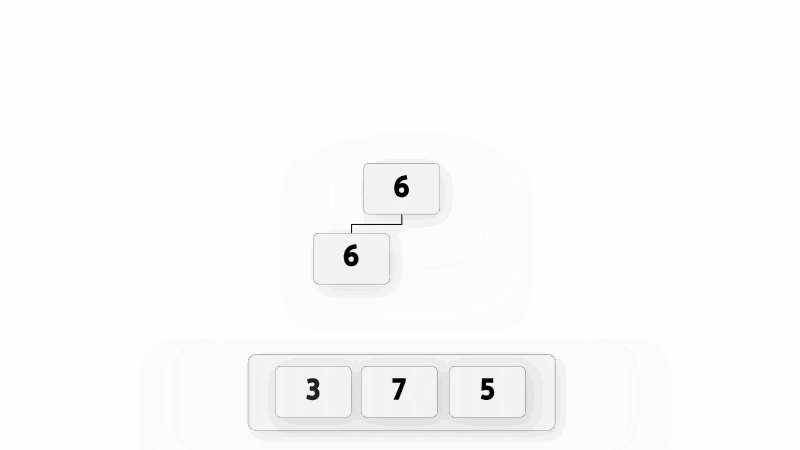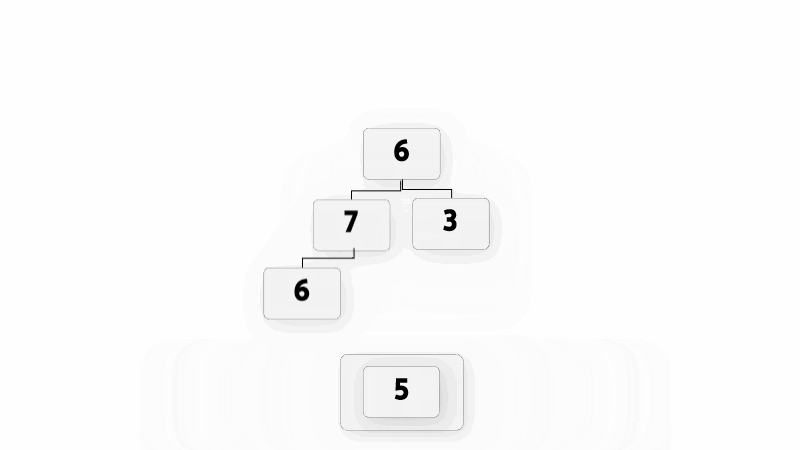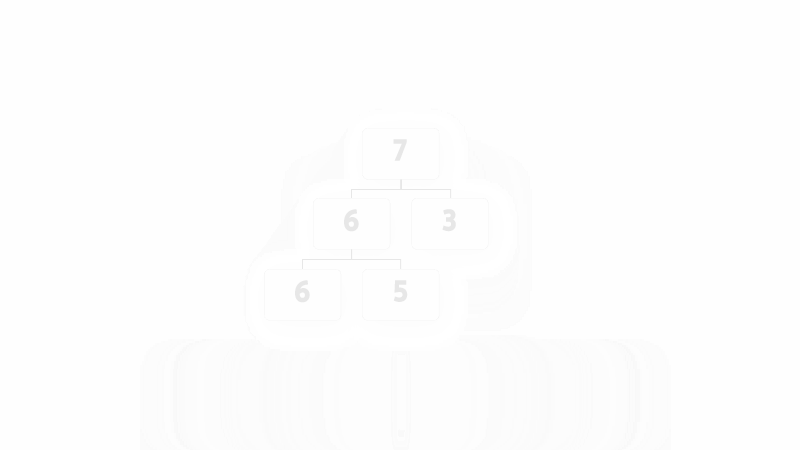
solve()
类似于插入操作的设计思想, 要对堆中的元素进行修改, 可以先直接修改, 然后再去维护堆.
1/ 分配智慧果
将堆中最大元素, 即堆顶元素减一, Bonez 的智慧果数量加一. 完成对智慧果数量的修改
2/ 调整元素位置, 保持堆的结构
整体的思想和流程和insert()的基本一致. 不同的是在插入的过程中维护是自底向上的, 而在这次维护的过程中调整是自顶向下的.
具体来说, 先判断修改后的堆是否还维持着堆的结构.
int solve()
{
int ret = 0; // 记录分配的次数, 即 Bonez 拿到的智慧果数量
// 重分配智慧果
while (_head < _heap[0]) //循环, 直到 Bonez 的智慧果数量比堆中的最大元素还大
{
// 1. 进行一次智慧果分配
_heap[0]--; _head++; ret++;
// 2. 调整元素位置, 保持堆的结构
// 自顶向下遍历检查
// (这里的 buf 和之前的 buf 不同: buf 是 scan 中更大的子节点的下标)
for (int scan = 0, buf = 1; buf < _size; buf = _LChild(scan))
{
// 找出子节点中更大的那个
if (buf + 1 < _size && _heap[buf] < _heap[buf + 1]) // if (下标不越界 && 另一个子节点更大)
buf++;
if (_heap[scan] > _heap[buf]) // 堆结构已经正确, 退出循环.
break;
swap(_heap[scan], _heap[buf]); // 交换节点, 使其满足堆的结构.
scan = buf; // 更新 scan, 以继续向子节点迭代检查.
}
print();
}
还是刚才的那个例子. 下面是在优先队列中的演示.
代码 codes
#include <iostream>
using namespace std;
class BinaryHeap // 大根堆
{
int *_heap = nullptr; // 存储堆中的所有元素
int _size = 0; // 堆中元素的数量
int _capacity = 0; // 堆的最大容量
int _head; // Bonez 的智慧果数量
// 用数组实现近似满二叉堆的相关接口
int _Parent(int x) { return ((x - 1) >> 1); }
int _LChild(int x) { return ((x << 1) + 1); }
int _RChild(int x) { return ((x << 1) + 2); }
public:
// 初始化
BinaryHeap(int c = 100000) : _capacity(c) { _heap = new int[c + 100]; }
void init(int h) { _head = h; }
void insert(int n)
{
// 1. 插入新元素至堆底
_heap[_size++] = n;
// 2. 调整元素位置, 保持堆的结构
int buf, scan = _size - 1; // scan 从堆底开始扫描; buf 是 scan 的父节点用来判断堆结构是否正确
while ((buf = _Parent(scan)) >= 0) // 循环, 直到 scan 的父节点非零的时候退出
{
if (_heap[scan] < _heap[buf]) // 堆结构已经正确, 退出循环.
break;
swap(_heap[scan], _heap[buf]); // 交换节点, 使其满足堆的结构
scan = buf; // 更新 scan, 以继续向根节点迭代检查.
}
}
int solve()
{
int ret = 0; // 记录分配的次数, 即 Bonez 拿到的智慧果数量
// 重分配智慧果
while (_head < _heap[0]) //循环, 直到 Bonez 的智慧果数量比堆中的最大元素还大
{
// 1. 进行一次智慧果分配
_heap[0]--; _head++; ret++;
// 2. 调整元素位置, 保持堆的结构
// 自顶向下遍历检查
// (这里的 buf 和之前的 buf 不同: buf 是 scan 中更大的子节点的下标)
for (int scan = 0, buf = 1; buf < _size; buf = _LChild(scan))
{
// 找出子节点中更大的那个
if (buf + 1 < _size && _heap[buf] < _heap[buf + 1]) // if (下标不越界 && 另一个子节点更大)
buf++;
if (_heap[scan] > _heap[buf]) // 堆结构已经正确, 退出循环.
break;
swap(_heap[scan], _heap[buf]); // 交换节点, 使其满足堆的结构.
scan = buf; // 更新 scan, 以继续向子节点迭代检查.
}
print();
}
return ret;
}
void print()
{
for (int i = 0, j = 1; i < _size; i++)
{
if (i + 1 == j)
{
putchar('\n');
j *= 2;
}
printf("%d ", _heap[i]);
}
cout << endl;
}
};
inline int read();
int main(void)
{
#ifdef LOCAL_COMPILE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int numCount = read();
BinaryHeap heap(numCount);
heap.init(read());
for (int i = 1; i < numCount; i++)
heap.insert(read());
cout << heap.solve();
return 0;
}
inline int read()
{
int ret = 0, sign = 1;
char ch = getchar();
while (ch < '0' || ch > '9')
{
if (ch == '-')
sign = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
ret = (ret << 1) + (ret << 3) + (ch ^ 48);
ch = getchar();
}
return ret * sign;
}
