小孩的游戏 - 2021数据结构 排序和选择实验题
小孩的游戏 - 2021数据结构 排序和选择实验题
pre 做都做了, 干脆发上来算了 : D
题目分析
算法与数据结构实验题 5.18 小孩的游戏
★实验任务
一群小孩子在玩游戏,游戏规则是这样子,给了一些卡片,上面有数字,现在要把卡片按照某一种序列排好,让这些数字重新链接组合成一个大数,求最大的数是什么。
★数据输入
第一行一个整数N
接下来 N 行,每行一个整数 \(a_i\),为第 i 张卡片上的数值。\((0\le a_i \le 100)\)
50%数据 \(1\le N\le 50000\)
100%数据\(1\le N\le 100000\)
★数据输出
输出重新组合好的大数。
输入示例 3 99 23 99
输出示例 999923
题目分析
-
注意到虽然数据的数量很多, 但是数据的大小不是很大. 因此考虑使用计数排序.
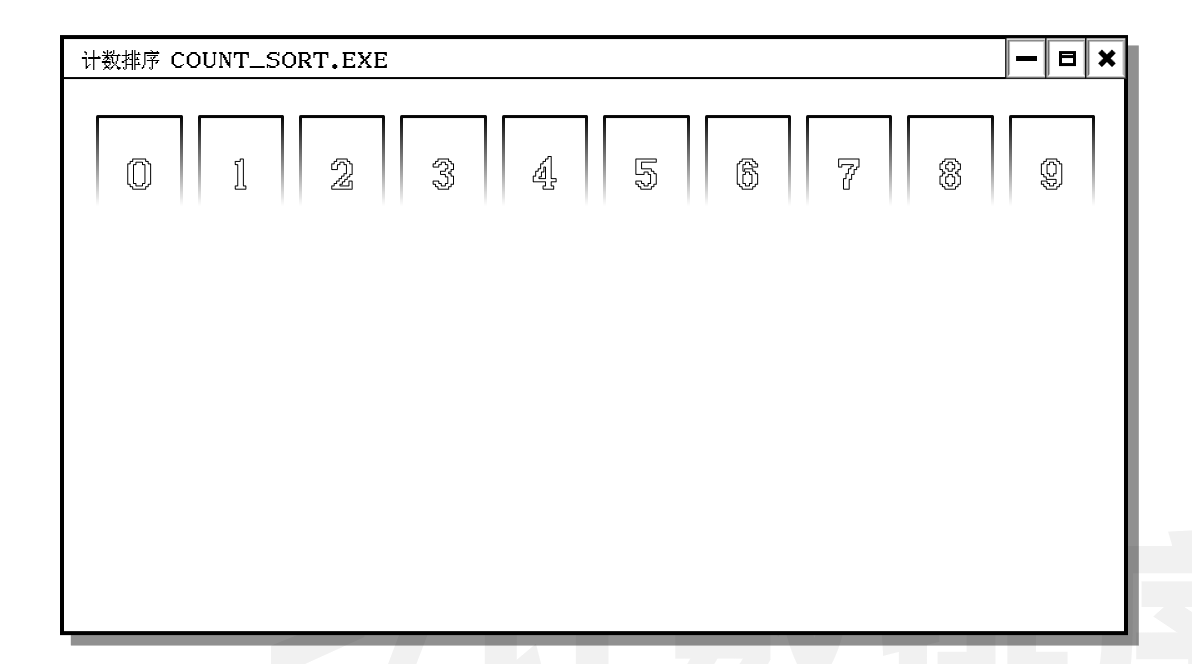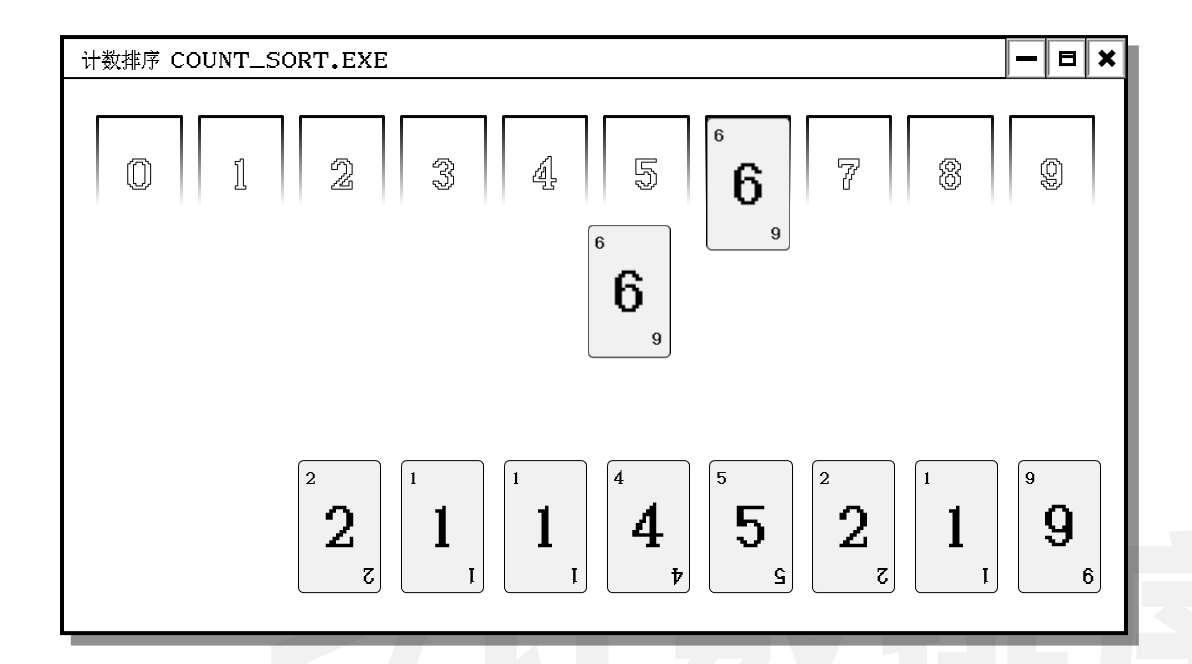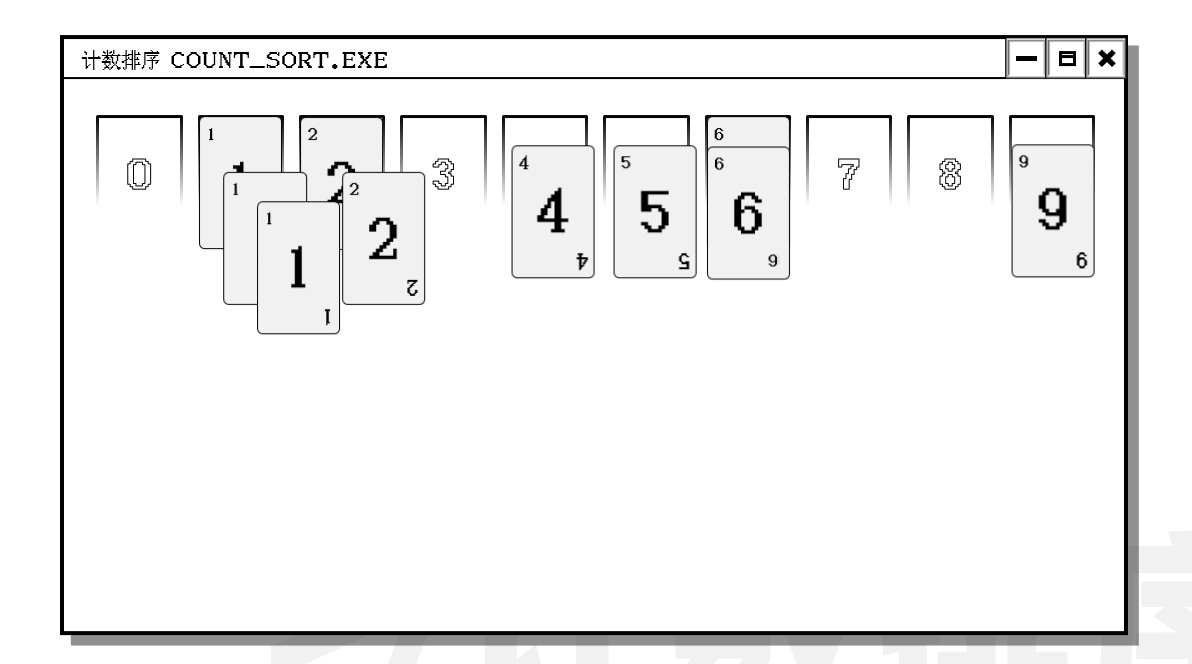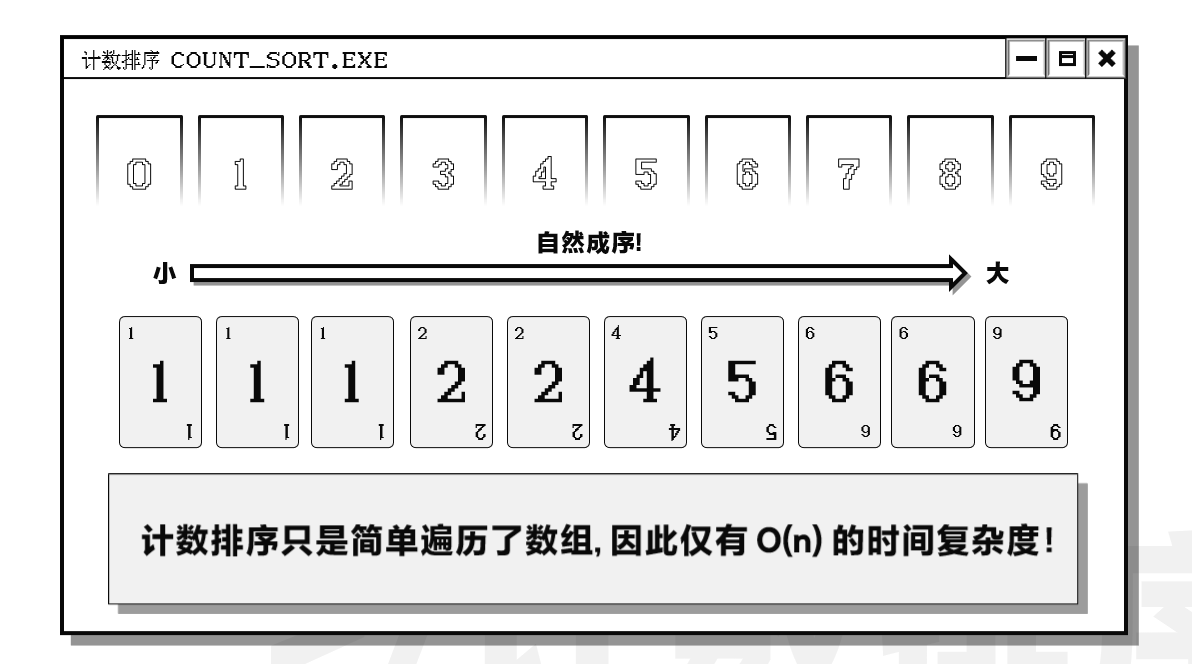
-
第一次写的时候把题目想简单了, 因为刚做完第一道题目就觉得这道题和之前的一样.
乍一看这题就是实现一个排序算法, 那就直接计数排序然后输出不就好了吗? 然而并没有那么简单, 考虑如下样例.

输入数据: [96, 9]
输出 ??
按照之前我以为的按序输出的想法的话, 应该会输出 96 9, 也就是 969
但其实这些数字能够组成的最大的数字是 9 96, 也就是 996.
这个样例说明了, 输出的数据之间的排序顺序不是简单的按照从大到小的顺序输出的, 而是存在一个优先级. 这个优先级是按照各个数位上的数字的大小来排序的.
我们都知道一个数字的大小是根据高数位上的数字的大小来判断的. 只要存在一个高位上的数字大于另一个数字上高位上的数字, 那么这个数字就一定大于另一个数字.
即高位数字越大的数字, 应当在输出中越靠前
也就是说组成的大数应当是能使高位数字越大的数据越靠前. 回到之前的样例之中, 9 是个个位数他越靠前能组成的数字也就越大. 虽然96在数值上大于9, 但96同时作为一个两位数也使得第二高为上的数字固定成了6. 这比9来的小.
所以个位数9的优先级反而会高于96的优先级.
代码实现
到这里, 这题就可以有两种思路.
-
思路 1
可以自定义一个compare函数, 判断两个元素正序连接起来的数字大还是倒序连接起来的数字大, 在这个样例里就是判断 "969" 和 "996" 哪个大, 然后通过STL库里的sort函数来完成这个排序. 这个方法是根据定义来写的, 可以适用于更大的数据范围, 同时也可以避免特别多奇奇怪怪的问题. 但这种方式在效率不是很高, 受限于库调用的排序算法, 此外compare函数的开销也比一般的比较开销来的大. 时间复杂度应该是 O(nlogn).
但是呢, 因为这道题目的数据范围是比较小的(0-100), 我们就有另一种方法, 也就是我这份代码使用的方法.
-
思路 2
生成每个可能的输入(1-100)在输出中的优先级, 并将优先级存到一个数组中, 接着按照这个生成的优先级即可输出正确结果.

确定了大致思路之后, 我们就有了一段伪代码.
int main(void)
{
// 初始化 & 输入数据
int n, bucket[101] = {0};
cin >> n;
for (int i = 0; i < n; i++)
bucket[read()]++;
// 生成优先级
int priority[101];
for (int i = 0; i > 101; i++)
// 生成并存入 priority[i]
// 按优先级输出
for (int i = 0; i <= 100; i++)
if (bucket[priority[i]])
for (int j = 0; j < bucket[priority[i]]; j++)
cout << priority[i];
}
输入和输出都是挺简单的吧, 重点就是如何生成优先级.
我们需要来研究一下优先级要怎么生成, 根据之前的讨论我们知道了要让数字越大也就是要让高位的数字越大.
根据这个原理, 我们可以对 0-100 这101个数字重新进行排序.
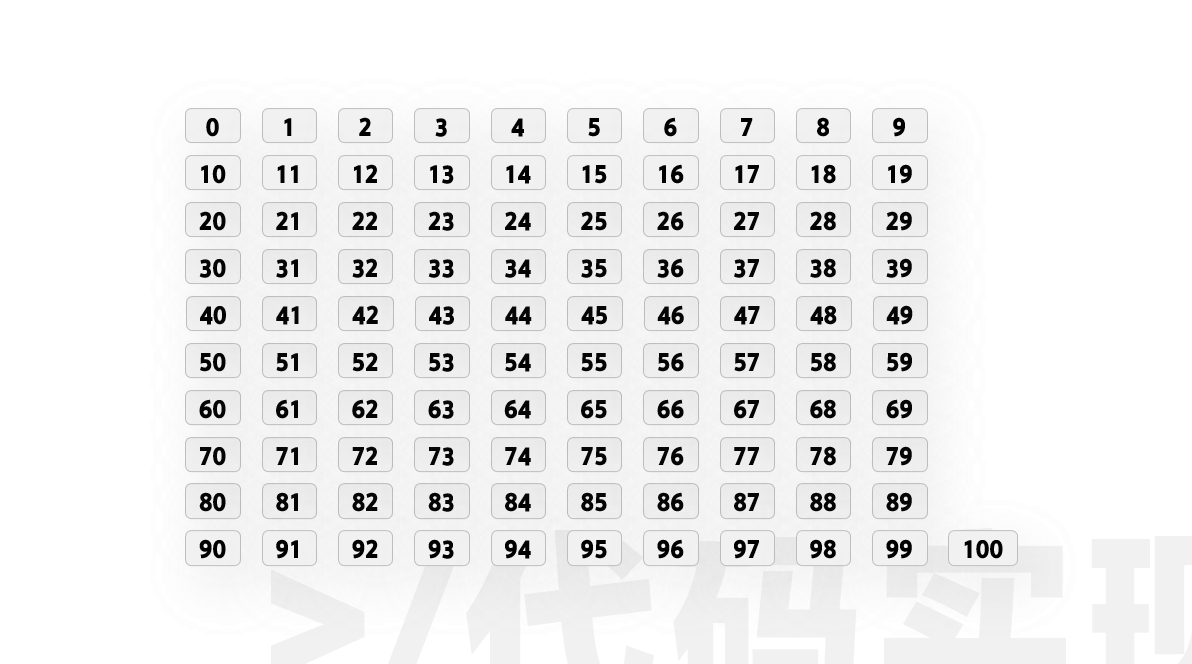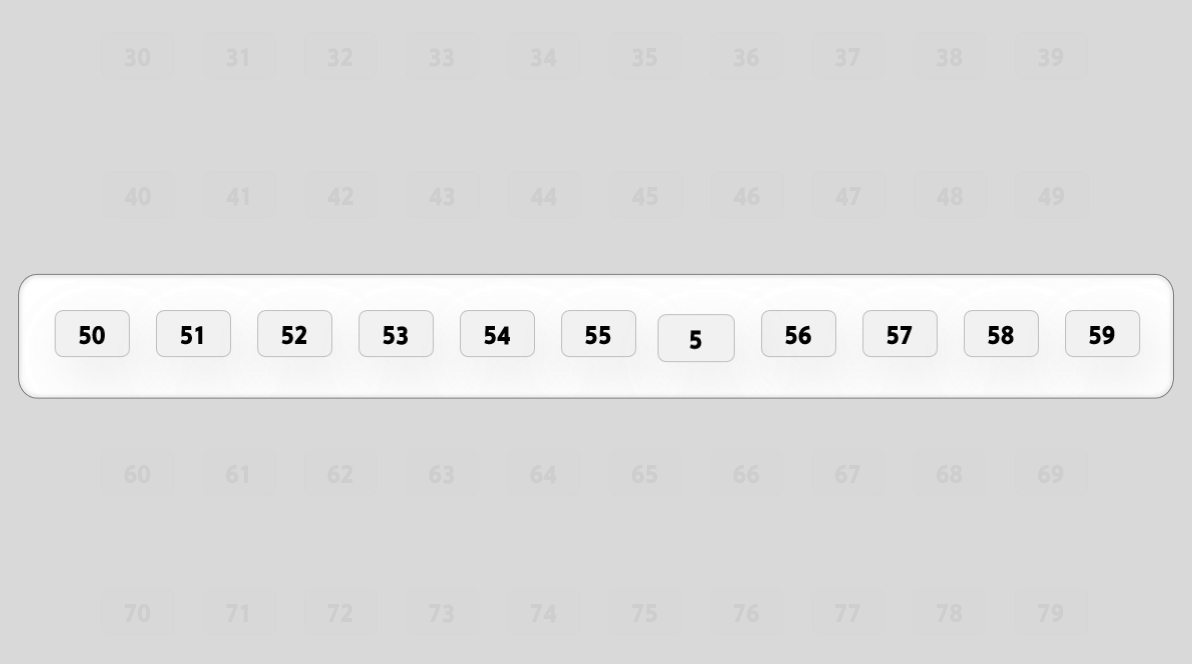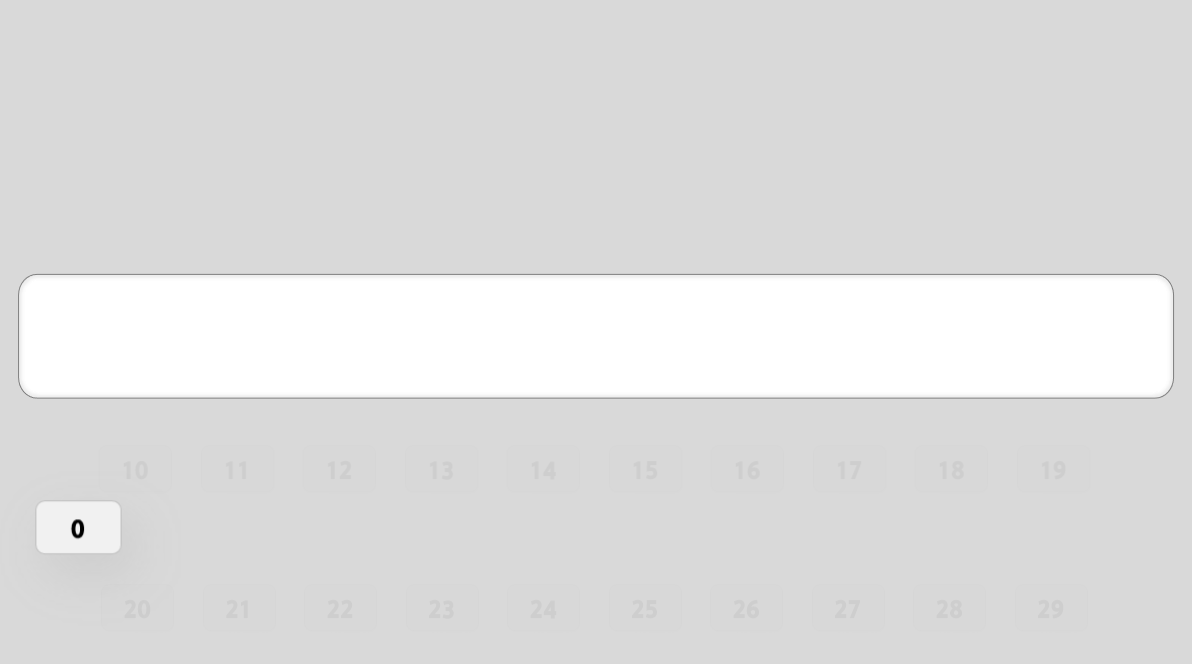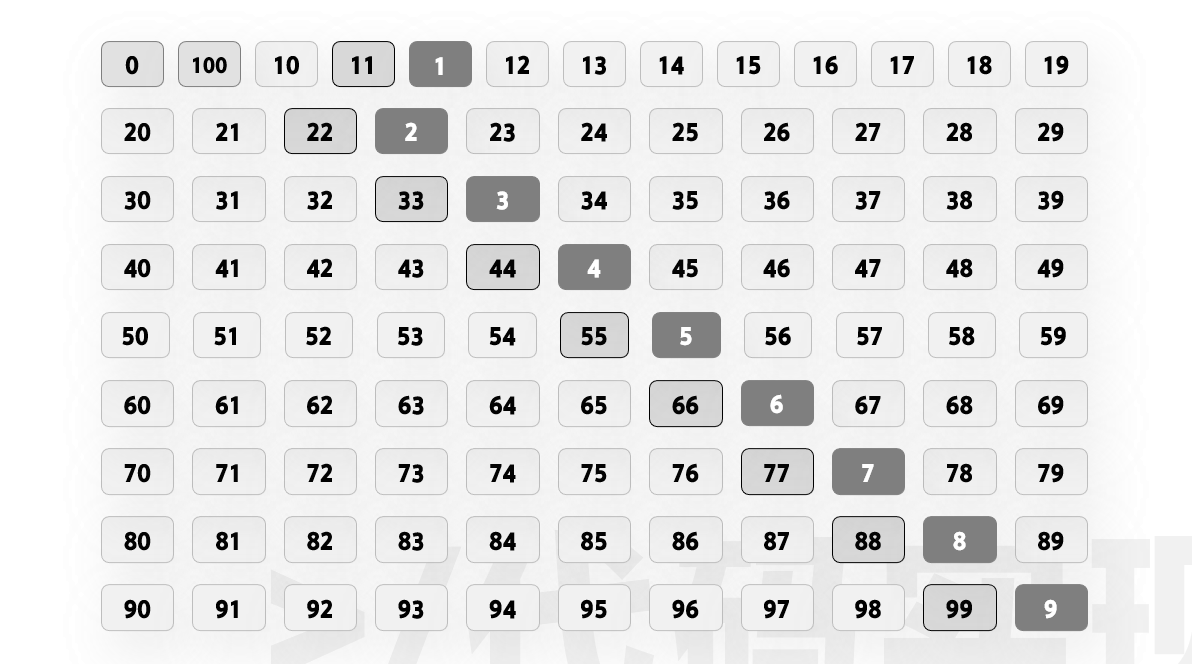
将这个过程转换成代码就有.
// 生成优先级
int priority[101];
int cnt = 0;
for (int i = 9; i > 0; i--)
for (int j = 9; j >= 0; j--)
{
if (i == j) priority[cnt++] = i;
priority[cnt++] = i * 10 + j;
}
priority[99] = 100;
priority[100] = 0;
两个 for 循环分别遍历十位数和个位数. 如同在前面的演示中所示, 当遇到个位数和十位数相同的时候, 插入一个对应的个位数, 完成 1-99 优先级的生成.
最后, 再最后补上两个特殊数字的优先级.
这个方法也存在它的局限性: 只能应对较小的数据范围, 对于更大的数据范围不好处理!
好了, 把伪代码改成真正的代码, 这道题目就完成了.
int main(void)
{
// 初始化 & 输入数据
int n, bucket[101] = {0};
cin >> n;
for (int i = 0; i < n; i++)
bucket[read()]++;
// 生成优先级
int priority[101];
int cnt = 0;
for (int i = 9; i > 0; i--)
for (int j = 9; j >= 0; j--)
{
if (i == j)
priority[cnt++] = i;
priority[cnt++] = i * 10 + j;
}
priority[99] = 100;
priority[100] = 0;
// 按优先级输出
for (int i = 0; i <= 100; i++)
if (bucket[priority[i]])
for (int j = 0; j < bucket[priority[i]]; j++)
cout << priority[i];
}
算法之外
快读函数!
相比 scanf() , cin 读入数字, 快读函数比他们快很多 (即使关闭流同步的情况下).
由于 cin 与 scanf() 需要对输入流进行格式化等操作, 在仅有数字输入的题目中会重复地消耗不必要的开销.
快读函数通过调用 getchar() 底层操作, 不进行不必要的操作, 对优化有大量数字输入的题目有奇效!
性能测试
| 读入方式 | DS测试用时(ms) |
|---|---|
| cin | 9 |
| scanf() | 14 |
| 快读函数 | 48 |
代码如下
inline int read()
{
int ret = 0, sign = 1;
char ch = getchar();
// 忽略无关字符 & 判断数字符号
while (ch < '0' || ch > '9'){
if (ch == '-') sign = -1;
ch = getchar();
}
// 计算输入数字大小
while (ch >= '0' && ch <= '9'){
ret = ret * 10 + (ch - '0');
ch = getchar();
}
return ret * sign;
}

