KMP算法学习小结

解决的问题

KMP算法用于解决字符串子串问题：给定一个待匹配串s和模式串p，要求算法返回s中第一次出现p的位置；若s中不存在p，则返回-1。

暴力解法

对于子串匹配问题，最简单的方法就是暴力解法。

• 从s的第1个字符开始，和p的第1个字符比较，若不相同则s左移（也就是变成判断s的第2个字符和p的第1个字符）。
• 当字符匹配时，则判断后续字符是否完全相同，如果完全相同则匹配成功。
• 如果没有完全匹配成功，则回到此次在s中找到的p的第1个字符的位置，在该位置的后一个位置继续和p的首字符匹配。

暴力解法逻辑简单，容易理解和实现，但时间复杂度为N平方，效率很低。暴力解法效率低的原因就在于，当子串匹配失败时，每次都要回到s中此次子串判断的起点的下一个位置。但是根据p的特点，并不是每一次都需要回到判断起点。每次匹配失败后的最佳目标跳转位置只由p来决定（和公共前后缀有关）。

KMP的核心

比如s：aabaabaac，p：aabaac。第一次匹配失败是在s的第6个字符b和p的第6个字符c，按照暴力解法，应该回到s的第2个字符a和p的第1个字符a的判断，但是此后每次都只能成功匹配第一个字符，直至匹配到s的第6个字符b和p的第3个字符b，才能成功匹配2个字符。但是在第一次匹配失败时，事实上就已经相当于知道s中匹配失败位置前5个字符和p的前5个字符是相同的，而通过此信息事实上可以确定匹配失败后最佳的比较位置是s的第6个字符b和p的第3个字符b。

KMP算法的核心就是利用每次匹配失败后已知的信息，让下一次转到已知的最佳位置进行判断。这个最佳位置利用next数组来存储。而next数组的计算，只跟p有关。

每次判断失败后，我们都希望跳过尽可能多的无效匹配操作，而这是可以通过确定最长公共前后缀来确定的。暴力法其实就是不断地尝试确定这个最长公共前后缀。但前面已经说过，在每次匹配失败的位置之前的字符其实是可以确定的。所以，只要能够确定1个已知串的最长公共前后缀，就能够得出next数组。

next数组的求解

在子串匹配问题中的最长公共前后缀问题又很特殊。在第k个字符匹配失败，显然就是截取出前k-1个字符的公共前后缀。很容易确定的是，长度为1的串不存在公共前后缀。长度为2的串只有在第1个字符和第2个字符相同时，才能够得到最大值1。而长度为3的串，显然就是在长度为2的串后面加上一个字符，即使最长公共前后缀取得最大值，也只能够比长度为2的公共前后缀大1。

此时我们发现，如果我们要求next[i]，是可以利用next[i-1]来确定的。因为next数组的第1、2个位置必然知晓，为-1和0（也可以是0和1，具体取决于next数组的定义）。所以计算next是从前到后，利用已知确定未知的。

以下next数组从下标0开始计算。当求解next[i]时，必然已知next[i-1]的值，假设为a。那么根据next数组的定义，在p[i-1]之前，必然存在a个字符，同p[0]开始的a个字符相同。此时，如果p[a]和p[i-1]相同，那么字符p[i]之前的最大公共前后缀的长度也就是a+1，即next[i]的值为next[i-1]+1。而如果p[a]和p[i-1]不相同，则表示需要进行回溯。那么我们下面就需要根据next[a]的值所提供的信息来继续判断了，假设next[a]的值为b。

而为什么要利用next[a]的值呢？其实也就是结合next数组表达的含义，利用所有已知的信息不断回溯。可以参考下面的示意图。

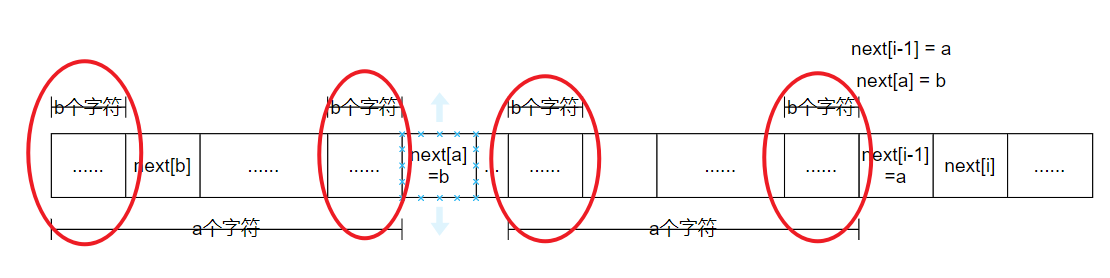
next[a]=b的含义就表示p[a]前的b个字符，和从p[0]开始的b个字符相同。而由于p[a]前的a个字符已经可以确定和p[i-1]前的a个字符相同，所以图中标识出来的四个部分完全相同，其中最重要的就是确定第一处标识和最后一处标识这两部分相同。那么根据此前的判断，如果p[b]和p[i-1]相同，则next[i]的值也就等于next[b]+1。若还不相等，则继续回溯，利用next[b]的值所提供的的信息继续判断。

重复如此判断，一直到取到next中的某个值等于-1。因为-1提供的信息无法继续回溯了，也就表示不可能存在公共前后缀了，就把next[i]的值置为-1。

根据next数组表达的是匹配失败跳转回字符串的第k的字符，或是跳转到下标为k的位置，next数组的数值会有所不同（具体就是整体相差1），但大同小异。

这是看完B站的一个讲解next数组求解算法的视频中理解到的。这里做个小结和记录，原视频链接如下：https://www.bilibili.com/video/BV16X4y137qw?from=search&seid=16229221945449574172&spm_id_from=333.337.0.0 。另参考了LeetCode算法书《字符串和数组》的介绍：https://leetcode-cn.com/leetbook/read/array-and-string/cpoo6/ 。