组合数学初步
组合数学初步
基本计数原理
加法原理：若完成一个事件 \(A\) 有 \(n\) 类方法，第 \(i\) 类有 \(s_i\) 种不同的方案，则完成事件 \(A\) 有 \(\sum^{n}_{i=1} s_i\) 种方案。
乘法原理：若完成一个事件 \(A\) 需要 \(n\) 步，第 \(i\) 步有 \(k_i\) 种不同的方式，则完成事件 \(A\) 有 \(\prod_{i=1}^{n}k_i\) 种不同的方案。
减法（简单容斥）原理：若完成事件 \(A\) 共有 \(n\) 次尝试，其中 \(c\) 次不能完成，则其中能完成的次数为 \(n-c\)。
排列
从 \(n\) 个人中选 \(m\) 个人排成一排，问方案数。
解：
第一个人有 \(n\) 种选择，第二个人有 \(n-1\) 种选择……第 \(m\) 个人有 \(n-m+1\) 种选择。
分步乘法得 \(\prod _{i=1}^m n-i+1=\frac{n!}{(n-m)!}\)，记为 \(A_n^m\)。
组合
从 \(n\) 个人中选 \(m\) 个人，问方案数。
解：无需排成一排，把重复的去掉即可。
答案为 \(\frac{n!}{m!(n-m)!}\)，记为 \(C_n^m\) 或者 \(\tbinom{n}{m}\)。
性质：
-
\(C_n^m=C_n^{n-m}\)。
-
\(\sum_{i=0}^n=2^n\)。
-
\(\forall k>0,C_n^k=C_{n-1}^k+C_{n-1}^{k-1}\)。
-
\(C_{n}^m=C_{n-1}^{m-1}\times \frac{n}{m}\)。
-
\(\sum_{i=1}^n C_{i+m}^i=C_{m+n+1}^{m+1}-1\)
证明：
组合数的一般求法
- 暴力乘
时间复杂度 \(O(n)\)。
1.\(T\) 组数据，每次求 \(C_n^m \bmod p\)，\(p\) 固定，\(m,n\le 10^3\)。
- 杨辉三角递推
根据归纳恒等式：
可以递推，预处理 \(O(n^2)\)，单次 \(O(1)\)。
int C[N][N];
C[0][0]=1;
FOR(i,1,n) {
C[i][0]=1;
FOR(j,1,n) C[i][j]=C[i][j-1]+C[i-1][j-1];
}
2.\(T\) 组数据，每次求 \(C_n^m \bmod p\)，\(p\) 固定，\(m,n\le 10^5\)。
- 预处理阶乘
在取模时需要求逆元。
预处理 \(O(n)\)，单次复杂度 \(O(1)\)。
int C(int n,int m) {
if(n<m) return 0;
return fac[n]*inv[m]%Mo*fac[n-m]%Mo;
}
fac[0]=1;
FOR(i,1,n) fac[i]=fac[i-1]*i%Mo;
inv[n]=power(fac[i],Mo-2);
ROF(i,n,1) inv[i-1]=inv[i]*i%Mo;
3.求 \(C_n^m \bmod p\)，\(n,m\le 10^{18},p\le 10^5,p\in \mathbb{P}\)。
- 卢卡斯定理
若 \(p\) 为质数，则有：
证明：
引理：\(p\in \mathbb{P},x^p+1\equiv (x+1)^p\pmod p\)
证明：后者用二项式定理展开：
\[(x+1)^p=\sum_{i=0}^p C_p^i x^i=(\sum_{i=1}^{p-1} C_p^i x^i) + 1 + x^p \]显然，括号内均为 \(p\) 的倍数，可消掉。
证毕。
设 \(n=ps+c,m=pt+d\)
故原命题等价于求证 \(C_n^m=C_s^t\times C_c^d\)。
\(C_n^m\) 在 \((1+x)^n\) 中等价于 \(x^m\) 的系数。
在 \(\bmod p\) 意义下，\((1+x)^p\equiv 1+x^p \pmod p\)。
根据二项式定理，有：
\[\begin{aligned} &\hspace{0.6cm} (1+x)^n\\ &=(1+x)^{ps+c}\\ &=(1+x)^{ps}\times (1+x)^c\\ &=(\sum_{i=0}^s C_s^i x^{ip})\times (\sum_{i=0}^c C_c^i x^i) \end{aligned} \]又 \(x^m=x^{pt+d}=x^{pt}\times x^d\)。
因为 \(s<p\)，所以后面不可能提供 \(x^{pt}\)，前面也不可能提供 \(x^{d}\)。
故 \(x^m\) 一定是两式相乘而得。
故原命题成立。
证毕。
const int N=1e5+10;
int t,fac[N];
LL power(LL a,LL b,LL p) {
LL res=1;
for(;b;b>>=1) {
if(b&1) res=(res*a)%p;
a=a*a%p;
}
return res%p;
}
LL C(int n,int m,int p) {
if(n<m) return 0;
return fac[n]*power(fac[m],p-2,p)%p*power(fac[n-m],p-2,p)%p;
}
LL lucas(int n,int m,int p) {
if(n<p&&m<p) return C(n,m,p);
return C(n%p,m%p,p)*lucas(n/p,m/p,p)%p;
}
int n,m,Mo;
void solve() {
cin>>n>>m>>Mo;n=n+m;
FOR(i,1,Mo) fac[i]=fac[i-1]*i%Mo;
cout<<lucas(n,m,Mo)<<"\n";
}
main() {
cin>>t;fac[0]=1;
while(t--) solve();
return 0;
}
预处理 \(O(p)\)，单次 \(O(\log n)\)。
- 求 \(C_n^m\)，\(n,m\le 10^3\),不取模
高精度除法直接秒了！
发现无论除的是什么 妖魔鬼怪，最后总会是一个非负整数。
所以考虑对阶乘分解质因数，将除法算式转化为质数幂的指数相减的形式。
最后只需要做高精度乘法了。
单次复杂度 \(O(n)\)。
(本代码以洛谷P1771为例)
const int N=1e5+10;
int n,x,v[N],phi[N];
vector<int>prime;
LL power(LL a,LL b,LL p) {
LL res=1%p;
for(;b;b>>=1) {
if(b&1) res=(res*a)%p;
a=(a*a)%p;
}
return res;
}
void Euler() {
phi[1]=1;
FOR(i,2,100000) {
if(!v[i]) phi[i]=i-1,v[i]=i,prime.pb(i);
for(int p:prime) {
if(i*p>100000||v[i]<p) break;
v[i*p]=p;
phi[i*p]=phi[i]*(i%p?p-1:p);
}
}
}
int sum[N];
int Get(int x,int p) {
int cnt=0;
while(x) {
cnt+=x/p;
x/=p;
}
return cnt;
}
vector<int>Mul(vector<int>x,int y) {
LL tol=0;vector<int>res;
for(auto c:x) {
tol+=(LL)y*c;
res.pb(tol%10);
tol/=10;
}
while(tol) res.pb(tol%10),tol/=10;
return res;
}
main() {
cin>>n>>x;
x=power(x,x,1000);
Euler();
for(auto p:prime) sum[p]=Get(x-1,p)-Get(n-1,p)-Get(x-n,p);
vector<int>ans;ans.pb(1);
for(auto p:prime) while(sum[p]--) ans=Mul(ans,p);
reverse(ans.begin(),ans.end());
for(auto x:ans) write(x);putchar('\n');
return 0;
}
- 求 \(C_n^m \bmod p\) 的值，其中 \(n,m\le 10^9\)，\(p\) 不一定为质数，但保证 \(p\) 的所有质因子幂次均为 \(1\)。
将 \(p\) 分解质因数，分别求出原式对 \(p\) 的各个质因子取模的结果。
最后用 中国剩余定理 解同余方程组即可。
(这里以洛谷 P2840 为例)
const int Mo=999911659,N=4e4+10;
int p[4]={2,3,4679,35617},M[4],t[4],a[4],inv[N],fac[N];
int n,g;
int power(int x,int y,int p) {
int res=1;
for(;y;y>>=1) {
if(y&1) res=res*x%p;
x=x*x%p;
}
return res;
}
int C(int n,int m,int p) {
if(n<m) return 0;
return fac[n]*inv[m]%p*inv[n-m]%p;
}
int Lucas(int n,int m,int p) {
if(n<p&&m<p) return C(n,m,p);
return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;
}
vector<int>c;
void Init(int id) {
int P=p[id];
fac[0]=1;
FOR(i,1,P-1) fac[i]=fac[i-1]*i%P;
inv[P-1]=power(fac[P-1],P-2,P);
ROF(i,P-1,1) inv[i-1]=inv[i]*i%P;
for(int x:c) (a[id]+=Lucas(n,x,P))%=P;
}
int Crt() {
int m=Mo-1;
FOR(i,0,3) M[i]=m/p[i],t[i]=power(M[i],p[i]-2,p[i]);
int ans=0;
FOR(i,0,3) (ans+=a[i]*M[i]%m*t[i]%m)%=m;
return ans;
}
int solve() {
for(int i=1;i*i<=n;++i) {
if(n%i) continue;
c.pb(i);
if(i==n/i) continue;
c.pb(n/i);
}
FOR(i,0,3) Init(i);
return Crt();
}
main() {
cin>>n>>g;
if(g==Mo) {
puts("0");
return 0;
}
cout<<power(g,solve(),Mo)<<"\n";
return 0;
}
- 求 \(C_n^m \bmod p\) 的值，其中 \(p\) 不一定为质数，\(n,m\le 10^5\)。
跟高精度的思想差不多，乘的时候顺带取模就行了，代码不放了。
- 求 \(C_n^m \bmod q\) 的值，其中 \(n,m\le 10^{18},q\le 10^6\)
这个刺激了
类似上述思想，将 \(q\) 分解质因数，设 \(q\) 的唯一分解为 \(p_1^{c_1}p_2^{c_2}p_3^{c_3}\dots p_o^{c_o}\)。
求出同余方程组
问题转换成如何求出 \(C_n^m \bmod p^c\) 的值。
这个式子等价于：
这玩意没办法用逆元，考虑转化。
由于 \(p^c\) 仅有一个本质不同的质因子 \(p\)，考虑在 \(m!\) 与 \((n-m)!\) 除掉 \(p\) 的若干次幂，使得分母与模数互质，这样就可以用扩展欧几里得求逆元了。
但是，剩下被除掉的部分还是不和模数互质，故还需要在分子上除掉若干次幂消掉分子的被除掉的贡献。
这样式子就变成了
问题转换成求 \(\frac{n!}{p^x}\)。
注意到上面的 \(p^{\lfloor\frac{n}{p}\rfloor}\) 最后一定要被除掉，并发现上述 \(\lfloor\frac{n}{p}\rfloor!\) 还可能有 \(p\) 因子存在，故设递推式：
这样求解目标就是 \(f(n)\)，递归边界为 \(f(0)=1\)。
问题转换成求 \(f(n)\) 后面带的那一串乘法算式。
注意到后面的所有乘数都不是 \(p\) 的倍数，所以 \(l<p^c,l,p^c+l,2p^c+l\dots (\lfloor\frac{n}{p^c}\rfloor-1)\times p^c+l\) 其实在 \(\bmod p^c\) 意义下是等价的，都是 \(l\)。
所以只求小于 \(p^c\) 部分的乘积，中间部分直接对小于 \(p^c\) 的部分做快速幂，剩下的 \(\lfloor\frac{n}{p^c}\rfloor\times p^c \sim n\) 的部分暴力乘即可。
求一次 \(f(n)\) 复杂度是 \(O(p^c \log n)\) 的，这个 \(\log\) 是以 \(p\) 为底的，所以比一般的 \(\log\) 要小。
int f(int n,int p,int pk) {
if(!n) return 1;//边界
int st=1,ed=1;
FOR(i,1,pk) if(i%p) (st*=i)%=pk;//暴力求开始部分
st=power(st,n/pk,pk);//快速幂求中间贡献
FOR(i,pk*(n/pk),n) if(i%p) (ed*=(i%pk))%=pk;//余项
return f(n/p,p,pk)*st%pk*ed%pk;//递归求解n/p
}
问题来了，怎么求 \(p^{x-y-z}\)?
其实就是求 \(n!\) 中有多少 \(p\) 这个质因子。
事实上，在 \(f(n)\) 的过程中，已经顺便求出来了。
\(p^{\lfloor\frac{n}{p}\rfloor}\times \lfloor\frac{n}{p}\rfloor!\times (1\times 2\times 3\dots)\)
的这个 \(p^{\lfloor\frac{n}{p}\rfloor}\)，将递归过程中的 \(\lfloor\frac{n}{p}\rfloor\) 加起来就行了。
int g(int x,int p) {//求 x! 中有多少 p
int cnt=0;
while(x) {
cnt+=x/p;
x/=p;
}
return cnt;
}
求出 \(f(n)\) 本身与 \(f(m),f(n-m)\) 在 \(\bmod p^c\) 意义下的逆元，乘起来后对 \(p^c\) 取模就是 \(C_n^m \bmod p^c\)。
int inv(int a,int p) {
int x,y;
exgcd(a,p,x,y);
return (x+p)%p;
}
int C(int n2,int m2,int p,int pk) {
int nc=f(n2,p,pk),mc=inv(f(m2,p,pk),pk),nmc=inv(f(n2-m2,p,pk),pk);//n!,1/m!,1/(n-m)!
int pa=power(p,g(n2,p)-g(m2,p)-g(n2-m2,p),pk);//p^(x-y-z)
return nc*mc%pk*nmc%pk*pa%pk;//乘积。
}
最后，使用中国剩余定理合并方程组，即可求出答案，总时间复杂度 \(O(q \log n)\)。
int exLucas() {
int nw=p;
for(int i=2;i*i<=p;++i) {
if(nw%i) continue;
int cy=0;
while(nw%i==0) ++cy,nw/=i;
vec.pb(mkp(i,cy));
}
if(nw>1) vec.pb(mkp(nw,1));
for(auto o:vec) {
int x=o.fr,y=o.se,pk=1;
FOR(i,1,y) pk*=x;
crt.pb(mkp(C(n,m,x,pk),pk));
}
int m=1,ans=0;
for(auto o:crt) m*=o.se;
for(auto o:crt) {
int x=o.se,M=m/x;
int l,r;exgcd(M,x,l,r);
l=(l+m)%m;
(ans+=l%m*M%m*o.fr%m)%=m;
}
return ans;
}
全部代码如下：
const int N=1e6+10;
int n,m,p,M[N];
void exgcd(int a,int b,int &x,int &y) {
if(!b) return x=1,y=0,void();
exgcd(b,a%b,x,y);
int t=x;x=y;y=t-(a/b)*y;
}
int mul(int a,int b,int p) {
int res=0;a%=p,b%=p;
for(;b;b>>=1) {
if(b&1) res=(res+a)%p;
a=a*2LL%p;
}
return res;
}
int power(int a,int b,int p) {
int res=1%p;a%=p;
for(;b;b>>=1) {
if(b&1) res=mul(res,a,p)%p;
a=mul(a,a,p)%p;
}
return res;
}
int f(int n,int p,int pk) {
if(!n) return 1;
int st=1,ed=1;
FOR(i,1,pk) if(i%p) (st*=i)%=pk;
st=power(st,n/pk,pk);
FOR(i,pk*(n/pk),n) if(i%p) (ed*=(i%pk))%=pk;
return f(n/p,p,pk)*st%pk*ed%pk;
}
int g(int x,int p) {
int cnt=0;
while(x) {
cnt+=x/p;
x/=p;
}
return cnt;
}
int inv(int a,int p) {
int x,y;
exgcd(a,p,x,y);
return (x+p)%p;
}
int C(int n2,int m2,int p,int pk) {
int nc=f(n2,p,pk),mc=inv(f(m2,p,pk),pk),nmc=inv(f(n2-m2,p,pk),pk);
int pa=power(p,g(n2,p)-g(m2,p)-g(n2-m2,p),pk);
return nc*mc%pk*nmc%pk*pa%pk;
}
vector<pair<int,int> >vec,crt;
int exLucas() {
int nw=p;
for(int i=2;i*i<=p;++i) {
if(nw%i) continue;
int cy=0;
while(nw%i==0) ++cy,nw/=i;
vec.pb(mkp(i,cy));
}
if(nw>1) vec.pb(mkp(nw,1));
for(auto o:vec) {
int x=o.fr,y=o.se,pk=1;
FOR(i,1,y) pk*=x;
crt.pb(mkp(C(n,m,x,pk),pk));
}
int m=1,ans=0;
for(auto o:crt) m*=o.se;
for(auto o:crt) {
int x=o.se,M=m/x;
int l,r;exgcd(M,x,l,r);
l=(l+m)%m;
(ans+=l%m*M%m*o.fr%m)%=m;
}
return ans;
}
main() {
cin>>n>>m>>p;
cout<<exLucas()<<"\n";
return 0;
}
讲个笑话，扩展 lucas 和 lucas 没有任何关系。
组合数经典问题
直接求很不好做。
考虑上面的减法原理，用总数减去不会越狱的方案数。
总数显然是 \(m^n\)。
而不会越狱当且仅当相邻两个监狱的信仰不同。
所以第一个可以有 \(m\) 种选择，第二个可有 \(m-1\) 种选择（不能选第一个人选的），第三个有 \(m-1\) 种选择（不能选第二个人的）……
所以答案为 \(m^n-m\times (m-1)^{n-1}\)。需要注意减法取模的情况。
例2.错排问题
设 \(f(n)\) 表示当排列长度为 \(n\) 时该问题答案。
考虑递推，假设 \(n\) 放在了第 \(k\) 个位置，则有 \(n-1\) 种选择。
则此时第 \(k\) 个信封有两种选择：
-
放在第 \(n\) 个位置，则剩余 \(n-2\) 个再次错排，有 \(f(n-2)\) 种方案。
-
不放在第 \(n\) 个位置，则剩余 \(n-1\) 个错排，有 \(f(n-1)\) 种方案。
上述先放 \(n\)，再放 \(k\)，分两步，用乘法原理。第二步分两类，用加法原理。
则 \(f(n)=(n-1)\times (f(n-1)+f(n-2))\)。
先选几个固定后，剩下的错排即可。
\(n,m\) 很小，使得我们可以杨辉三角递推组合数。
注意到 \(k\) 固定，所以递推时可以对 \(k\) 取模，一个组合数能够整除 \(k\) 当且仅当该数字 \(\bmod k\) 后为 \(0\)。
最后做二维前缀和即可做到每次 \(O(1)\) 查询。
例5.方程的解
给你一个不定方程 \(\sum _{i=1}^k x_i =g(n)\)，求正整数解个数。
首先，\(g(n)\) 可以通过快速幂得到。
考虑这样一个问题：
给你 \(n\) 个相同的球与 \(k\) 个不同的盒子，每个盒子至少放一个，求将这 \(n\) 个球全部放入 \(k\) 个盒子的方案数。
将这 \(n\) 个球排成一排，最左侧和最右侧分别放上一个板子，如下：
这样问题转换成放入 \(k-1\) 个板子（不算两边的板子），两个板子之间至少有一个球，求方案数。
如下即为一个 \(k=3\) 的合法方案：
最终每个盒子放入的球就是两个板子之间的球的数量。
注意到球之间共有 \(n-1\) 个空隙，我们只要在选择 \(k-1\) 个空隙，对每个空隙分别插入一个板子就一定能够构造出一个合法方案。
问题转换成从 \(n-1\) 个东西中选出 \(k-1\) 个东西，求方案数。
答案很显然了，\(C_{n-1}^{k-1}\)！
回到上面的问题，我们抽象一下，将 \(g(x)\) 个 \(1\) 排成一排，有 \(k\) 个数，初始为 \(0\)，每个数要选择一些 \(1\) 加到自己上面，不能不选，求方案数。
这不就是放球问题吗？
这样问题就完美解决，答案即为 \(C_{g(x)-1}^{k-1}\)。
不过，该题没有模数，需要写高精。
扩展：给定不定方程 \(\sum_{i=1}^{k} x_i=n\)，求非负整数解的个数。
直接求显然不好做。
考虑做一些数学变换。
上面的 \(y_i\) 是换元的 \(x_i+1\)。
发现 \(y_i\) 的取值与 \(x_i\) 一一对应。
所以我们求出 \(y_i\) 的解数就可以求出 \(x_i\) 的解数。
而因为 \(y_i\ge 1\)，所以这题做完了。
例6.[USACO09FEB] Bulls And Cows S
枚举放多少头公牛，假设放 \(p\) 头。
则母牛剩下 \(n-p\) 头。
问题变成放 \(p\) 个板子隔成，左、右留的位置无限制，但板子之间必须空 \(k\) 个以上。
写成不定方程的形式就是
考虑像换元一样，将左边除左右两边的所有项减去 \(k\)，原式可化为：
这样就是不定方程非负整数解板子了，放置公牛 \(p\) 个的答案即：
最终答案即：
按原式计算即可。
例7.车的放置
先考虑一个 \(n\) 行 \(m\) 列的普通矩形放 \(k\) 个怎么做。
首先肯定是在 \(m\) 行中选 \(k\) 列，方案数为 \(C_m^k\)。
其次，选第一个所占得行时有 \(n\) 种方案，第二个有 \(n-1\) 种。
所以方案数有 \(C_m^k\times A_n^k\) 种。
接着将原图形分成两个矩形，这里设分成 \(a\times b\) 与 \((a+c)\times d\) 的矩形。
先放第一个，枚举放多少个（设为 \(k\) 个），方案有 \(C_a^k\times A_b^k\) 种。
再放第二个，设第二个放了 \(z\) 个，但是放第二个时由于第一个放 \(k\) 个后第二个的行只有 \(a+c-k\) 个了。
所以方案数是 \(C_{a+c-k}^z\times A_d^z\)。
乘起来就是答案。
一个 \(N\times M\) 的网格上有 \((N+1)\times (M+1)\) 个格点，为了叙述方便，以下记 \(n=N+1,m=M+1\)。
先不考虑不在同一条直线上的限制，就是在所有点中任选 \(3\) 个，方案显然有 \(C_{nm}^3\) 种。
考虑在此基础上减掉不合法的方案。
显然，不合法方案分成横着、竖着、斜着的。
对于横着，一共 \(n\) 行，每一行都有 \(C_m^3\) 种方案，乘起来即可。
竖着的同理。
斜着的有两种情况：斜率正与斜率负。
显然他们是对称的，即方案数相同。
只需要求出斜率为正的方案，最终乘 \(2\) 即可。
注意到我们可以枚举两个不在同一水平线且不在同一竖直线上的点，这样它们中间的点的个数（不包括两端）就是答案。
因为任选中间的一个点与两端的两个点总是可以在同一水平线上。
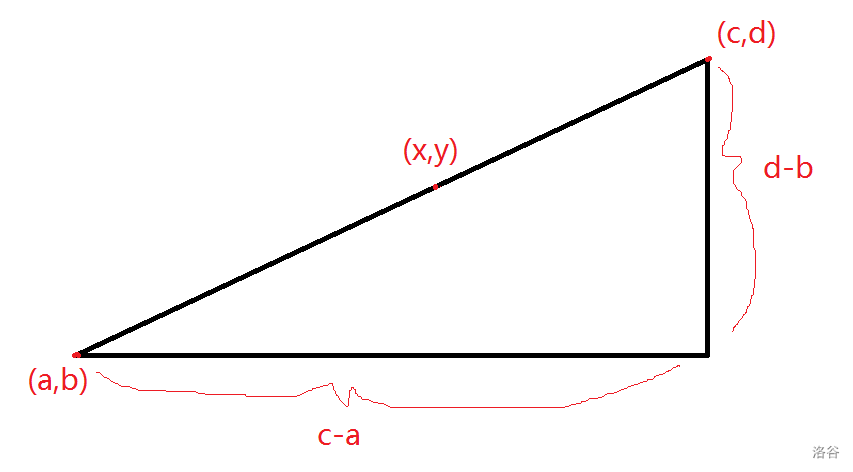
引理：在格点上，若一个点坐标为 \((a,b)\)，另一个点坐标为 \((c,d)\)，则它们连线上格点个数（不包括两端）为：
\[\gcd(|a-c|,|b-d|)-1 \]证明：
为叙述方便，以下把绝对值去掉。
对于斜边上任意一点 \((x,y)\)，满足 \(\frac{y-b}{x-a}=\frac{d-b}{c-a},x\in[a,c],y\in[b,d]\)。
来一张图。
记 \(g=\gcd(d-b,c-a)\)。
则：
\[\begin{aligned} &\hspace{-0.23cm}y=\frac{d-b}{c-a}\times (x-a)+b\\ &=\frac{\frac{d-b}{g}}{\frac{c-a}{g}}\times (x-a)+b\\ &=\frac{d-b}{g}\times \frac{x-a}{\frac{c-a}{g}}+b \end{aligned} \]若 \(y\in \mathbb{N}\)，则 \(\frac{c-a}{g}\mid{x-a}\)。
则一定存在一个 \(q\)，使得 \(\frac{c-a}{g}\times q=x-a\)。
则 \(x=\frac{c-a}{g}\times q+a\)。
经过一堆不等式变换后（或者按原不等式取值范围）得到 \(\frac{c-a}{g}\times q+a\in[a,c]\)。
最终得到 \(q\in[0,g]\cap\mathbb{Z}\)。
即 \(q\) 最多有 \(g+1\) 种取值，即最多有 \(g+1\) 种合法的 \(x\)。
掐头去尾即可证明原命题。
证毕。
直接枚举斜边的端点，计算即可。
事实上，直接枚举是 \(O(n^2m^2 \log n)\) 的，需要进一步优化。
实际上，我们固定形状后，格子图中有多少个这类形状的三角形已经确定了。
假设底、高分别为 \(a,b\)，则数量显然为 \((n-a+1)\times (m-b+1)\)。
证明留给读者思考。
复杂度 \(O(nm \log n)\)
int ans,n,m,s[1010][1010],a[1010][1010];
int gcd(int x,int y) {
return y?gcd(y,x%y):x;
}
int calc(int x) {
return x*(x-1)*(x-2)/6;
}
main() {
cin>>n>>m;
LL c=(n+1)*(m+1);
ans=calc(c)-(m+1)*calc(n+1)-(n+1)*calc(m+1);
FOR(i,1,n+1) FOR(j,1,m+1) ans-=2LL*(gcd(i,j)-1)*(n-i+1)*(m-j+1);
cout<<ans<<"\n";
return 0;
}
多重集排列数
多重集是一种广义的集合。
普通的集合是不可重的，即集合中每个元素都不相同。
多重集是一种可重集合，可以表示成这么一种形式：
上述可重集 \(A\) 就是描述了一个集合内有 \(n_1\) 个 \(a_1\)、\(n_2\) 个 \(a_2\)…… \(n_k\) 个 \(a_k\)。
所谓排列数，就是求 \(A\) 有多少个本质不同的排列。
记 \(n=\sum_{i=1}^k n_i\)。
则上述问题的答案为：
简证：
不考虑数字相同的情况，共有 \(n!\) 种。
每一个相同的数字内部总共会有 \(n_i!\) 种，需要除掉。
证毕。
将 \(i\) 与 \(p_i\) 之间连有向边，容易发现一定会形成若干个有向环。
若交换完成，则一定是 \(n\) 个自环。
而最优解一定是每次交换都能够让至少一个数字复位，在图上的表现就是让一个大环断成两个小环。
设 \(f_i\) 表示让一个长为 \(i\) 的大环分解成 \(i\) 个自环的方案数。
再设 \(g(x,y)\) 表示将一个长为 \(x+y\) 的环分成长为 \(x\) 和长为 \(y\) 的环的方案数。
注意到若 \(x=y\)，\(g(x,y)=x\)，否则 \(g(x,y)=x+y\)。
因为第一种可能会有重复情况，画图即可理解，这里不再赘述。
有转移：
这样就完了。……吗？
不然，考虑上述乘法原理，我们先把 \(x\) 环消掉再做 \(y\) 环，显然漏了情况。
其实可以先将 \(x\) 环分成两个，再将 \(y\) 环分成两个……
交替着做也是一种方案！肿么办？
发现一个长为 \(x\) 的环操作次数必然是 \(x-1\)。
则上面的操作总数一共是 \(x+y-2\)，要从中选 \(x-1\) 次操作给第一个环，剩下的给第二个环，有多少方案？
这不就组合数吗！
或者也可以按多重集排列数理解，\(x-1\) 个 \(1\)，\(y-1\) 个 \(0\) 有多少排列方案。
最终答案是一样的。
所以真正的方程应为：
最后 dfs 找环贡献加起来就行。
但是这样时间复杂度是 \(O(n^2)\) 的，无法通过。
事实上，\(f\) 有个通项公式：
这样用快速幂就可以 \(O(n)\) 求出答案了。
等等……为啥是 \(O(n)\)？
设第 \(i\) 个环的长度为 \(l_i\)，一共有 \(k\) 个环。
则有 \(\sum_{i=1}^k l_i=n\ge \sum_{i=1}^k \log l_i\)。
所以千万不要预处理 \(f\) 数组！
const int N=1e5+10,Mo=1e9+9;
int n,cnt,col[N],ct[N];
LL inv[N],fac[N];
bool vis[N];
vector<int>e[N];
void dfs(int x) {
col[x]=cnt;
for(int y:e[x]) {
if(col[y]) continue;
dfs(y);
}
}
LL power(LL a,LL b) {
LL res=1;
for(;b;b>>=1) {
if(b&1) res=res*a%Mo;
a=a*a%Mo;
}
return res;
}
void solve() {
cin>>n;cnt=0;
FOR(i,1,n) {
int x=read();
e[x].pb(i);
}
FOR(i,1,n) if(!col[i]) ++cnt,dfs(i);
FOR(i,1,n) ct[col[i]]++;
LL ans=fac[n-cnt];
FOR(i,1,cnt) {
(ans*=inv[ct[i]-1])%=Mo;
if(ct[i]<2) continue;
(ans*=power(ct[i],ct[i]-2))%=Mo;
}
cout<<ans<<"\n";
FOR(i,1,n) e[i].clear(),ct[i]=col[i]=0;
}
main() {
fac[0]=1;
FOR(i,1,N-10) fac[i]=fac[i-1]*i%Mo;
inv[N-10]=power(fac[N-10],Mo-2);
ROF(i,N-10,1) inv[i-1]=inv[i]*i%Mo;
int t=read();
while(t--) solve();
return 0;
}
最后的问题，\(f_i\) 的通项是怎么来的？
观察可得、oeis大法
证明：
引理：有标号无根树的方案数为 \(n^{n-2}\)（Cayley 公式）。
证明：根据 Prüfer序列 的性质，任何长为 \(n-2\) 的值域为 \([1,n]\) 的序列都可以唯一确定成一棵有标号树。
根据乘法原理，方案数显然为 \(n^{n-2}\)。
证毕。
考虑一个有 \(n\) 个点的环，显然需要 \(n-1\) 次交换就可以分成 \(n\) 个自环。
假设有一张图 \(G\)，开始时没有边。
每次若交换 \(p_x,p_y\)，则将 \(x,y\) 之间连一条无向边。
显然，这个图不会出现环，否则一定是断开的环之间重连，一定不是最优解。
而又因为该图有 \(n-1\) 条边，所以操作完成后 \(G\) 必定是一棵树。
考虑将操作倒过来，不断让两个环之间交换，最后合成一个大环，这样就转化为在树上删边。
若将树的每条边给一个顺序，按照这个顺序进行删边并合并环，则最后得到的环一定是不变的。
根据引理，边没有顺序的有标号树有 \(n^{n-2}\) 棵，加上边的顺序后就是 \(n^{n-2}\times (n-1)!\)。
这样就把边有标号的环和边有标号的有标号树建立了一一对应关系。
又因为合并顺序不同的环在不考虑合并顺序的差异后均为原环，本质上是一样的，有重复。
所以要去重，要在原来基础上除掉边重复的方案即 \((n-1)!\)。
所以方案数就是 \(n^{n-2}\)。
证毕。
