C++位运算

位运算是指按二进制进行的运算。在系统软件中，常常需要处理二进制位的问题。C语言提供了6个位操作运算符。这些运算符只能用于整型操作数，即只能用于带符号或无符号的char,short,int与long类型。

 

C语言提供的位运算符列表：

运算符	作用	示例
&	按位与	两个操作数同时为1结果为1
|	按位或	两个操作数只要有一个为1，结果就为1
~	按位非	操作数为1，结果为0；操作数为0，结果为1
^	按位异或	两个操作数相同，结果为0；不相同结果为1
<<	左移	右侧空位补0
>>	右移	左侧空位补符号位

1、“按位与”运算符（&）

 　　按位与是指：参加运算的两个数据，按二进制位进行“与”运算。如果两个相应的二进制位都为１，则该位的结果值为1；否则为0。这里的1可以理解为逻辑中的true,0可以理解为逻辑中的false。按位与其实与逻辑上“与”的运算规则一致。逻辑上的“与”，要求运算数全真，结果才为真。若，A=true,B=true,则A∩B= true。

例如：3&5

3的二进制编码是11(2)。（为了区分十进制和其他进制，本文规定，凡是非十进制的数据均在数据后面加上括号，括号中注明其进制，二进制则标记为2）内存储存数据的基本单位是字节（Byte），一个字节由8个位（bit）所组成。位是用以描述电脑数据量的最小单位。二进制系统中，每个0或1就是一个位。将11（2）补足成一个字节，则是00000011（2）。5的二进制编码是101（2），将其补足成一个字节，则是00000101（2）。

按位与运算：

0	0	0	0	0	0	1	1	(2)

&

0	0	0	0	0	1	0	1	(2)

=

0	0	0	0	0	0	0	1	(2)

由此可知3&5=1。 

C++代码：

 

 编译执行结果如下：

 

 

 

 2、按位与的用途：

（1）清零

若想对一个存储单元清零，即使其全部二进制位为0，只要找一个二进制数，其中各个位符合一下条件：
原来的数中为1的位，新数中相应位为0。然后使二者进行&运算，即可达到清零目的。

例：

原数为43，即00101011（43），另找一个数，设它为148，即  10010100（148），将两者按位与运算：

0	0	1	0	1	0	1	1	(43)

&

1	0	0	1	0	1	0	0	(148)

=

0	0	0	0	0	0	0	0	(0)

C++源代码：

 

编译执行结果如下：

 

  

（2）取一个数中某些指定位

若有一个整数a(2byte),想要取其中的低字节，只需要将a与8个1按位与即可。

a 00101100 10101100

b 00000000 11111111

c 00000000 10101100

（3）保留指定位：

与一个数进行“按位与”运算，此数在该位取1。

 

例如：有一数84，即01010100（84），想把其中从左边算起的第3，4，5，7，8位保留下来，运算如下：

0	1	0	1	0	1	0	0	(84)

&

0	0	1	1	1	0	1	1	(59)

=

0	0	0	1	0	0	0	0	(16)

即：a=84,b=59

        c=a&b=16

创建cppshift&cut.cpp

C++源代码：

 

 执行结果如下:

 

 

3、“按位或”运算符（|）

两个相应的二进制位中只要有一个为1，该位的结果值为1。借用逻辑学中或运算的话来说就是，一真为真。

--例如：60（8）|17（8）,将八进制60与八进制17进行按位或运算。

0	0	1	1	0	0	0	0	(060)

|

0	0	0	0	1	1	1	1	(017)

=

0	0	1	1	1	1	1	1	(077)

C++源代码：

 

 

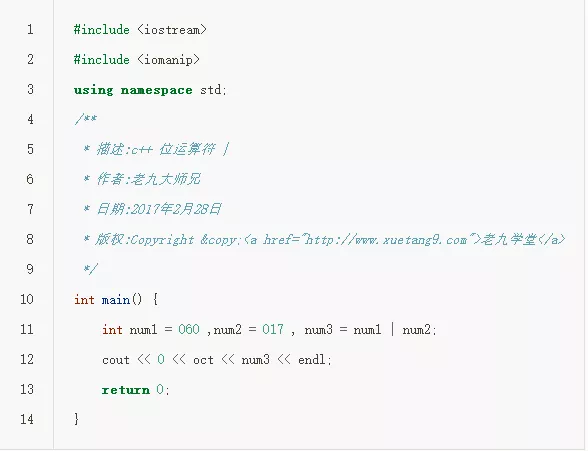
--编译执行代码得到的结果为:

 

 

--应用：按位或运算常用来对一个数据的某些位定值为1。

--例如：如果想使一个数a的低4位改为1，则只需要将a与17（8）进行按位或运算即可。

 

4、“异或”运算符（^）

--他的规则是：若参加运算的两个二进制位值相同则为0，否则为1，即0^0=0，0^1=1，1^0=1， 1^1=0。

--例：

0	0	1	1	1	0	0	1	(071)

^

0	0	1	0	1	0	1	0	(052)

=

0	0	0	1	0	0	1	1	(023)

--C++源代码：

 

 

--编译执行代码得到如下结果：

 

 

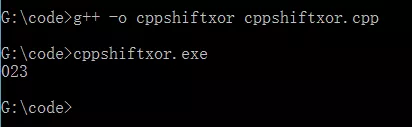
--应用：

 

(1)使特定位翻转

 

设有数01111010（2），想使其低4位翻转，即1变0，0变1.可以将其与00001111（2）进行“异或”运算，即：

0	1	1	1	1	0	1	0

^

0	0	0	0	1	1	1	1

=

0	1	1	1	0	1	0	1

运算结果的低4位正好是原数低４位的翻转。可见，要使哪几位翻转就将与其进行∧运算的该几位置为１即可。

 

(2)与0相“异或”，保留原值

例如：012^00=012

0	0	0	0	1	0	1	0	(012)

^

0	0	0	0	0	0	0	0	(00)

=

0	0	0	0	1	0	1	0	(012)

因为原数中的1与0进行异或运算得1，0^0得0，故保留原数。

 

(3)交换两个值，不用临时变量

 

例如：ａ＝3，即 1|1|（2)；ｂ＝４，即1|0|0（2）。
想将ａ和ｂ的值互换，可以用以下赋值语句实现：
ａ＝a^b;
ｂ＝b^a;
ａ＝a^b;
ａ＝011(2)
（^）ｂ＝100(2)
ａ＝111(2)（a^b的结果，a已变成７）
（^）ｂ＝100(2)
ｂ＝011(2)（b^a的结果，b已变成３）
（^）ａ＝111(2)
ａ＝100（2）（a^b的结果，a已变成４）

 

--等效于以下两步：
① 执行前两个赋值语句：“ａ＝ａ^ｂ；”和“ｂ＝ｂ^ａ；”相当于b=b^(a^b)；
② 再执行第三个赋值语句： ａ＝ａ^ｂ。由于a的值等于（ａ^ｂ），b的值等于（ｂ^ａ^ｂ），因此，相当于a=ａ^ｂ^ｂ^ａ^ｂ，即a的值等于ａ^ａ^ｂ^ｂ^ｂ，等于ｂ。很神奇吧！

 

--C++源代码：

 

 

 

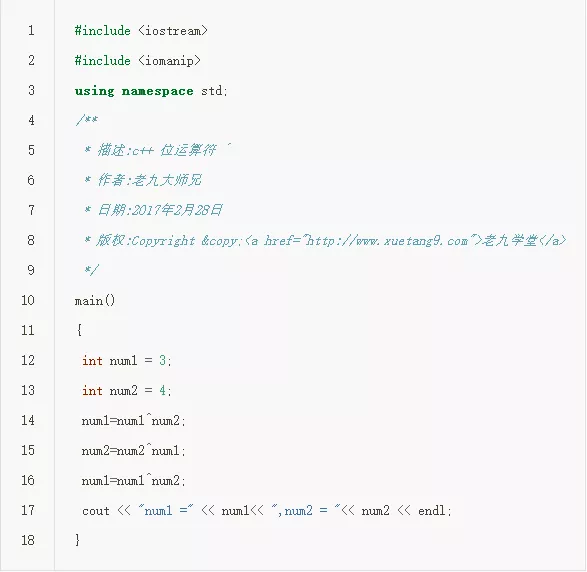
--编译执行后得到如下结果：

 

 

 

5、“取反”运算符（~）
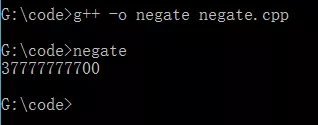
它是一元运算符，用于求整数的二进制反码，即分别将操作数各二进制位上的1变为0，0变为1。例如：~77(8)

--源代码：

 

 

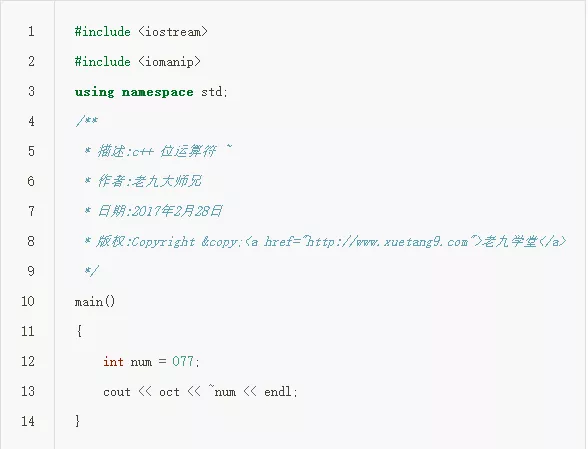
--编译执行之后得到结果如下：

 

 

 

6、左移运算符（<<）
左移运算符是用来将一个数的各二进制位左移若干位，移动的位数由右操作数指定（右操作数必须是非负值），其右边空出的位用0填补，高位左移溢出则舍弃该高位。

--例如：将a的二进制数左移2位，右边空出的位补0，左边溢出的位舍弃。若a=15,即00001111（2），左移2位得00111100（2）。

--源代码：

 

 

--编译执行后得到如下结果：

 

 

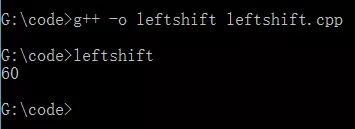
左移1位相当于该数乘以2，左移2位相当于该数乘以2*2＝4,15 << 2=60，即乘了4 。但此结论只适用于该数左移时被溢出舍弃的高位中不包含1的情况。
假设以一个字节（8位）存一个整数，若ａ为无符号整型变量，则ａ＝64时，左移一位时溢出的是0，而左移2位时，溢出的高位中包含1。

 

7、右移运算符（>>）

右移运算符是用来将一个数的各二进制位右移若干位，移动的位数由右操作数指定（右操作数必须是非负值），移到右端的低位被舍弃，对于无符号数，高位补0。对于有符号数，某些机器将对左边空出的部分用符号位填补（即“算术移位”），而另一些机器则对左边空出的部分用0填补（即“逻辑移位”）。

--注意：
对无符号数,右移时左边高位移入0；对于有符号的值,如果原来符号位为0(该数为正),则左边也是移入0。如果符号位原来为1(即负数),则左边移入0还是1,要取决于所用的计算机系统。有的系统移入0,有的系统移入1。移入0的称为“逻辑移位”,即简单移位；移入1的称为“算术移位”。

 

--例： a的值是八进制数113755，
a:1001011111101101 （用二进制形式表示）
a>>1: 0100101111110110 (逻辑右移时)
a>>1: 1100101111110110 (算术右移时)
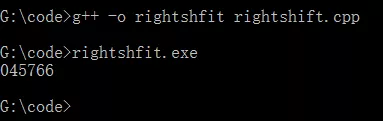
在有些系统中,a>>1得八进制数045766,而在另一些系统上可能得到的是145766。Turbo C和其他一些C编译采用的是算术右移,即对有符号数右移时,如果符号位原来为1，左面移入高位的是1。

 --源代码：

 

 

--编译执行后的结果如下：

 

 

8、位运算赋值运算符
位运算符与赋值运算符可以组成复合赋值运算符。
例如: &=, |=, >>=, <<=, ^=
例： a & = b相当于 a = a & b
a <<= 2 相当于 a = a << 2

--------------------------------------------------------------------------------------------------------------------------------------------------资料来源于“@老九学堂”-------------------------------------------------------------------------------------------------------------------------------