Record - NOIP模拟赛做题记录(1)
因为在某 OJ 上被删题了,甚至看不到自己交的代码了,所以就不订正了吧。
0715 模拟赛
A. 商店 shop(分治,背包)
题面
类似:[CF1442D Sum](https://www.luogu.com.cn/problem/CF1442D)商店中共有 \(N\) 种物品。
对于第 \(i\) 种物品,共有\(c_i\) 件,买这种物品的第一件时,价格为 \(a_i\),之后对于这种物品,每多买一件,价格都比前一件便宜 \(d_i\)。
现在,商店想要知道,如果有人想恰好买 \(M\) 件物品,最少要花多少钱。
第一行两个整数 \(N\), \(K\),表示物品种数和询问个数。
接下来 \(N\) 行,每行三个整数\(a_i\), \(d_i\), \(c_i\) 表示初始价格,每多买一件减少的价格和这件物品的数量。
接下来\(K\) 行,每行一个数\(m_i\),表示询问恰好买 \(m_i\) 物品最少要花的钱。
\(1 \leq N, K \leq 500, 1 \leq m_i \leq 20000, 1 \leq a_i, d_i, c_i \leq 10^9 , a_i > (c_i − 1) ∗ d_i\)
要买就尽量买完,且最多只有 \(1\) 类物品没有买完。
思路一
暴力枚举哪一类没有买完是不行的,分治递归那个区间有没买完的,将左半部分没买完和右半部分买完合并(01 背包),右半部分没买完和左半部分买完合并,取 \(\text{min}\)。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=505,M=20005;
const ll INF=0x3f3f3f3f3f3f3f3f;
int n,m,Q;
ll a[N],d[N],c[N],v[N];
ll dp[N][M];
void solve(int l,int r){
if(l==r){
for(int i=1;i<=20000;i++) dp[l][i]=INF;
ll tmp=0;
for(int i=1;i<=c[l];i++) tmp+=a[l]-(i-1)*d[l],dp[l][i]=tmp;
return;
}
int mid=l+r>>1;
solve(l,mid);
solve(mid+1,r);
for(int i=l;i<=mid;i++)
for(int j=20000;j>=c[i];j--)
dp[mid+1][j]=min(dp[mid+1][j],dp[mid+1][j-c[i]]+v[i]);
for(int i=mid+1;i<=r;i++)
for(int j=20000;j>=c[i];j--)
dp[l][j]=min(dp[l][j],dp[l][j-c[i]]+v[i]);
for(int i=1;i<=20000;i++)
dp[l][i]=min(dp[l][i],dp[mid+1][i]);
}
int main(){
scanf("%d%d",&n,&Q);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&a[i],&d[i],&c[i]);
c[i]=min(c[i],20000ll);
v[i]=(a[i]*c[i]-d[i]*c[i]*(c[i]-1)/2);
}
solve(1,n);
while(Q--){
scanf("%d",&m);
printf("%lld\n",dp[1][m]);
}
return 0;
}
思路二
参考 CF1442D 的题解,同样是分治,先 01 背包算出左半部分买完,递归右半部分,再还原并算出右半部分买完,递归左半部分。
递归到区间 \([l,r]\) 时,\([1,l-1] \cup [r+1,n]\) 都已被计算过,在递归到 \(l=r\) 的时候枚举选了多少更新答案即可。
D. 养护员 tree(max 卷积,线段树合并)
题面
给定一棵大小为 $n$ 的树,第 $i$ 个节点有点权 $w_i(1 \leq w_i \leq m)$,记树 上一个连通块 S 中最大的点权为 $maxS$,现在需要你求 $maxS = 1, 2, 3, \ldots, m$ 的连通块个数,答案对 $998244353$ 取模。第一行有 \(2\) 个整数 \(n, m\),含义在题目描述中给出。
第二行有 \(n\) 个整数,第 \(i\) 个代表 \(w_i\)。
接下来的 \(n − 1\) 行,每行两个整数 \(u, v\),描述树上的一条边 \((u, v)\)。
\(n,m \leq 2 \times 10^5\)
思路
40pts
考虑对于节点 \(u\) 维护 \(f_{u,i}\) 表示所有深度最小节点为 \(u\) 的连通块中最大点权为 \(i\) 的连通块个数,对于每个 \(k\),答案为 \(\sum_{i=1}^n f_{i,k}\)。
。
考虑孩子 \(v\) 和父亲 \(u\) 合并的过程中, \(f_{u,i} \leftarrow \sum_{max(j,k)=i} f_{u,j}f_{v,k}\),暴力转移复杂度为 \(O(nm^2)\)。
上述形式为 \(\text{max}\) 卷积,维护 \(g_{u,i}=\sum_{j=1}^i f_{u,i}\),那么 \(f_{u,i} \leftarrow g_{u,i}g_{v,i}-g_{u,i-1}g_{v,i-1}\),复杂度优化为 \(O(nm)\)。
100pts
使用线段树合并进行优化。但同时考虑到被合并的子树在跳过时会对答案做贡献,考虑递归往下时额外维护一个标记即可。
复杂度 \(O(n \log n)\)。
因为被删题直接放同学代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+10,mod=998244353;
const ll inf=0x3f3f3f3f3f3f3f3f;
ll n,m,w[N],ans[N];
ll s[N*20],lazy[N*20],lson[N*20],rson[N*20];
//s记录f
ll root[N],tot=0;
ll du[N];
ll head[N],cnt=0;
struct node{
ll v,nex;
}e[N*2];
void add(ll u,ll v){
e[++cnt].v=v;
e[cnt].nex=head[u];
head[u]=cnt;
}
void pushdown(ll now){
if(lazy[now]==1) return;
if(lson[now]){
s[lson[now]]=s[lson[now]]*lazy[now]%mod;
lazy[lson[now]]=lazy[lson[now]]*lazy[now]%mod;
}
if(rson[now]){
s[rson[now]]=s[rson[now]]*lazy[now]%mod;
lazy[rson[now]]=lazy[rson[now]]*lazy[now]%mod;
}
lazy[now]=1;
}
void change(ll &now,ll l,ll r,ll x){
if(!now){
now=++tot;
s[now]=0;
lazy[now]=1;
lson[now]=0;
rson[now]=0;
}
if(l==r){
s[now]=1;
return;
}
pushdown(now);
ll mid=(l+r)>>1;
if(x<=mid) change(lson[now],l,mid,x);
else change(rson[now],mid+1,r,x);
s[now]=(s[lson[now]]+s[rson[now]])%mod;
}
ll merge(ll u,ll v,ll l,ll r,ll sumu,ll sumv){//sumu记录u的线段树中f前缀和,sumv记录v的线段树中f前缀和
if(!u&&!v) return 0;
if(!u){//u中这个f不存在,只剩它的前缀和
s[v]=s[v]*sumu%mod;
lazy[v]=lazy[v]*sumu%mod;
return v;
}
if(!v){//v中这个f不存在,只剩它的前缀和
s[u]=(s[u]*sumv%mod+s[u])%mod;//u原本已经有答案了,所以要+1
lazy[u]=(lazy[u]*sumv%mod+lazy[u])%mod;
return u;
}
if(l==r){
s[u]=(s[u]+s[u]*sumv%mod+sumu*s[v]%mod+s[u]*s[v]%mod)%mod;
return u;
}
pushdown(u);
pushdown(v);
ll mid=(l+r)/2;
//由于先merge左子树可能会让左边s的值改变,所以先merge右子树
rson[u]=merge(rson[u],rson[v],mid+1,r,(sumu+s[lson[u]])%mod,(sumv+s[lson[v]])%mod);
lson[u]=merge(lson[u],lson[v],l,mid,sumu,sumv);
s[u]=(s[lson[u]]+s[rson[u]])%mod;
return u;
}
void ask(ll now,ll l,ll r){
if(!now) return;
if(l==r){
ans[l]=(ans[l]+s[now])%mod;
return;
}
pushdown(now);
ll mid=(l+r)>>1;
ask(lson[now],l,mid);
ask(rson[now],mid+1,r);
}
void dfs(ll u,ll fa){
change(root[u],1,m,w[u]);
for(int i=head[u];i;i=e[i].nex){
ll v=e[i].v;
if(v==fa) continue;
dfs(v,u);
root[u]=merge(root[u],root[v],1,m,0,0);
}
ask(root[u],1,m);
}
struct go_60pts{
ll p,b[N],num=0;
struct seg{
ll ss[N*4];
void build(ll k,ll l,ll r,ll b[]){
if(l==r){
ss[k]=b[l];
return;
}
ll mid=(l+r)>>1;
build(k*2,l,mid,b);
build(k*2+1,mid+1,r,b);
ss[k]=max(ss[k*2],ss[k*2+1]);
}
ll ask(ll k,ll l,ll r,ll x,ll y){
if(x<=l&&r<=y) return ss[k];
if(r<x||y<l) return -inf;
ll mid=(l+r)>>1;
return max(ask(k*2,l,mid,x,y),ask(k*2+1,mid+1,r,x,y));
}
}tree;
bool ck(){
ll count=0;num=0;
for(int i=1;i<=n;i++){
if(du[i]>2) return 0;
count+=(du[i]==1);
if(du[i]==1) p=i;
}
return count==2;
}
void dfs1(int u,int fa){
b[++num]=w[u];
for(int v,i=head[u];i;i=e[i].nex){
v=e[i].v;
if(v==fa) continue;
dfs1(v,u);
}
}
void solve(){
dfs1(p,p),tree.build(1,1,n,b);
for(int i=1;i<=n;i++){
ll l=1,r=i-1,p=i;ll sum=1;
while(l<=r){
ll mid=(l+r)>>1;
if(tree.ask(1,1,n,mid,i-1)<b[i]) p=mid,r=mid-1;
else l=mid+1;
}
sum*=(i-p+1);
l=i+1,r=n,p=i;
while(l<=r){
ll mid=(l+r)>>1;
if(tree.ask(1,1,n,i+1,mid)<=b[i]) p=mid,l=mid+1;
else r=mid-1;
}
sum*=(p-i+1);
(ans[b[i]]+=sum)%=mod;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
}
}go_60;
int main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
for(int i=1;i<=n-1;i++){
ll u,v;
cin>>u>>v;
add(u,v);
add(v,u);
du[u]++;
du[v]++;
}
if(go_60.ck()){
go_60.solve();
exit(0);
}
dfs(1,0);
for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
return 0;
}
0722 模拟赛
计数专场,start。
A. 难 nan(结论题)
题面
类似:[P7050 [NWRRC2015] Concatenation](https://www.luogu.com.cn/problem/P7050)题目:给定两个字符串 a, b,从 a 中选一段前缀,b 中选一段后缀(前后缀都可以为 空),并将选出的后缀拼在选出的前缀后面。 你需要求出有多少种本质不同的串(可以为空)。
\(|a|,|b| \leq 2 \times 10^5\)
思路
总方案数减去不合法的方案数。以 ab 和 bc 为例,abc 会重复;以 abb 和 bc 为例,abc 和 abbc 会重复。奇奇怪怪地就发现不合法的方案数就是 \(\sum_{i=a}^znum[i]*num2[i]\) 。
B. 交易 trade(折线计数,卡特兰数)
题目:\(n\) 天中价格为 \(1\) 金币或 \(2\) 金币,每天买入或卖出一件,或什么都不做,求有多少种价格方案使得最多能赚 \(k\) 元。
补习:卡特兰数
一种应用是从 \((0,0)\) 向上或向右走到 (n,n),不能走到 直线 \(y=x\) 上方,计数。
发现所有走到 \(y=x\) 以上的路径关于 \(y=x+1\) 可以与一条到达 \((n-1,n+1)\) 的路径对应(???),易得常见公式 \(H_n={2n \choose n}-{2n \choose n-1}\)。
思路
这是经典 trick,一定要记住。
考虑一个简化版 CF1924D,只包含 \(n\) 个左括号,\(m\) 个右括号的序列满足最长合法括号子序列长度为 \(k\),计数。
- 左括号视作 \(+1\),右括号视作 \(-1\),每种情况对应从 \((0,0)\) 到 \((n+m,n-m)\) 的折线,碰到 \(y=k-m\) 且位于 \(y=k-m\) 上,计数。
- 将红色折线碰到 \(y=k-m\) 后的部分翻折,得到蓝色折线,发现会有 \(k\) 次向上,用碰到 \(y=k-m\) 的减去碰到 \(y=k-m-1\) 的即为答案 \({n+m \choose k}-{n+m \choose k-1}\)。
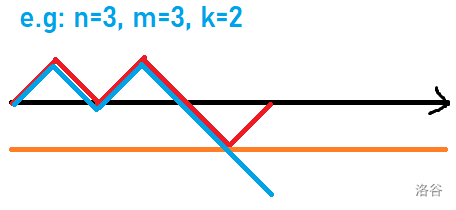
对于此题,视为从 \((0,0)\) 到达 \((0,n)\),每种情况,只有 \(2k\) 个操作是确定的,位于 \(y=0\) 以下的 \(n-2k\) 天什么也不做,通过样例发现答案要乘上 \(n-2k+1\) (懵)。
0723 模拟赛
原来之前一直有 std 代码呀,没发现,早知道就不玩雀魂了,悲。
搬题计数专场,continue。
B. 可重集 multiset(前缀和优化 DP)
C. 数排列 perm(容斥,可撤销 DP,莫队)
原题:AT_jsc2019_final_f
容斥,令满足 \(p_i=a_i\) 的 \(i\) 的集合为 \(S\),\(f_S\) 为方案数,则 \(ans=\sum_{S}(-1)^{|S|} f_S\)。
又让 $g_i \leftarrow \sum_{|S|=i} f_S $,则 \(ans=\sum_{i=0}^n (-1)^i g_i\)。
排列每个数出现一次(废话),\(g_i\) 实际上是所有颜色,有 \(i\) 个数和放的位置上的 a 相等的方案数,可以用 DP 求解。
颜色的枚举顺序并不影响最终结果,那么可以用可撤销 DP+莫队做。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2005,MOD=998244353;
int n,q,block,len;
int bk[N];
int a[N],cnt[N];
int jc[N],dp[N][N],ans[N];
struct Que{
int l,r,id;
}Q[N];
bool cmp(Que x,Que y){
return bk[x.l]==bk[y.l]?x.r<y.r:bk[x.l]<bk[y.l];
}
void ins(int x){
if(cnt[a[x]]){
for(int i=1;i<len;i++)
dp[len-1][i]=(dp[len][i]-1ll*dp[len-1][i-1]*cnt[a[x]]%MOD+MOD)%MOD;
}else ++len;
++cnt[a[x]];
for(int i=1;i<=len;i++)
dp[len][i]=(dp[len-1][i]+1ll*dp[len-1][i-1]*cnt[a[x]]%MOD)%MOD;
}
void del(int x){
for(int i=1;i<len;i++)
dp[len-1][i]=(dp[len][i]-1ll*dp[len-1][i-1]*cnt[a[x]]%MOD+MOD)%MOD;
--cnt[a[x]];
if(!cnt[a[x]]) --len;
else{
for(int i=1;i<=len;i++)
dp[len][i]=(dp[len-1][i]+1ll*dp[len-1][i-1]*cnt[a[x]]%MOD)%MOD;
}
}
int main(){
scanf("%d%d",&n,&q);
block=sqrt(n);
for(int i=1;i<=n;i++) bk[i]=(i-1)/block+1;
for(int i=1;i<=n;i++) scanf("%d",&a[i]),++a[i];
jc[0]=1;
dp[0][0]=1;
for(int i=1;i<=n;i++)
jc[i]=1ll*jc[i-1]*i%MOD,dp[i][0]=1;
for(int i=1;i<=q;i++){
scanf("%d%d",&Q[i].l,&Q[i].r);
++Q[i].l;
Q[i].id=i;
}
sort(Q+1,Q+q+1,cmp);
for(int i=1,l=1,r=0;i<=q;i++){
while(l>Q[i].l) ins(--l);
while(r<Q[i].r) ins(++r);
while(l<Q[i].l) del(l++);
while(r>Q[i].r) del(r--);
int tmp=0;
for(int j=0;j<=len;j++)
if(j&1) (tmp+=MOD-1ll*dp[len][j]*jc[n-j]%MOD)%=MOD;
else (tmp+=1ll*dp[len][j]*jc[n-j]%MOD)%=MOD;
ans[Q[i].id]=tmp;
}
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
return 0;
}
0726模拟赛
B. 好图 good(kruskal 生成树)
题面
给定 $n$ 个点 $m$ 条边的联通图,完全图的边数 $M=\frac{n(n-1)}{2}$,要求添加 $M-m$ 条边, $1 \sim M$ 恰好有一条边,且加边前后最小生成树的权值和不变,求是否存在合法方案。思路
模拟 kruskal 的过程,若原有边的两端的连通块 \(x,y\) 不连通,则 \(siz_x siz_y\) 减去已有的连接 \(x,y\) 的边都可以匹配更大的边权。
已有的连接 \(x,y\) 的边可以用类似启发式合并的方式求。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+5;
int n,m,fa[N];
vector<int>g[N];//联通块可到达
ll siz[N];
struct edge{
int x,y;
ll v;
bool f;
}e[N];
bool cmp(edge p,edge q){
return p.v<q.v;
}
int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
int main(){
freopen("good.in","r",stdin);
freopen("good.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;
for(int i=1;i<=m;i++){
scanf("%d%d%lld",&e[i].x,&e[i].y,&e[i].v);
g[e[i].x].push_back(e[i].y);
g[e[i].y].push_back(e[i].x);
}
sort(e+1,e+m+1,cmp);
ll now=0;
for(int i=1;i<=m;i++){
now-=e[i].v-e[i-1].v-1;
if(now<0){
puts("No");
return 0;
}
int x=find(e[i].x),y=find(e[i].y);
if(x==y) continue;
if(g[x].size()>g[y].size()) swap(x,y);
now+=siz[x]*siz[y];
for(int k:g[x]){
if(find(k)==y) --now;
g[y].push_back(k);
}
g[x].clear();
fa[x]=y;
siz[y]+=siz[x];
}
puts("Yes");
return 0;
}
参考资料
本文来自博客园,作者:雨中秋,转载请注明原文链接:https://www.cnblogs.com/zengzi/p/18319529,不然会AFO

