作业5-线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性。

监督学习中回归与分类的分别

 

线性回归，线性回归就是能够用一个直线较为精确地描述数据之间的关系，这样当出现新的数据的时候，就能够预测出一个简单的值。利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

 

 

 

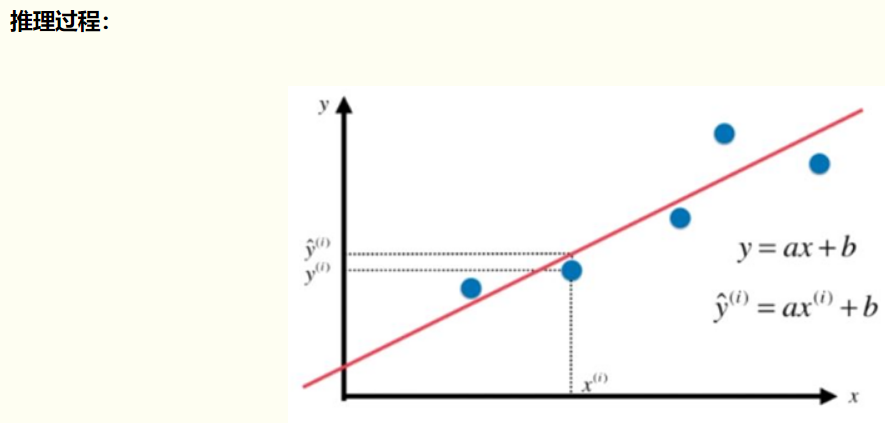
线性回归适用于X和y之间存在线性关系的数据集，可以使用计算机辅助画出散点图来观察是否存在线性关系。我们尝试使用一条直线来拟合数据，使所有点到直线的距离之和最小。线性回归中通常使用残差平方和，即点到直线的平行于y轴的距离而不用垂线距离，残差平方和除以样本量n就是均方误差。均方误差作为线性回归模型的损失函数。使所有点到直线的距离之和最小，就是使均方误差最小化，这个方法叫做最小二乘法。

 

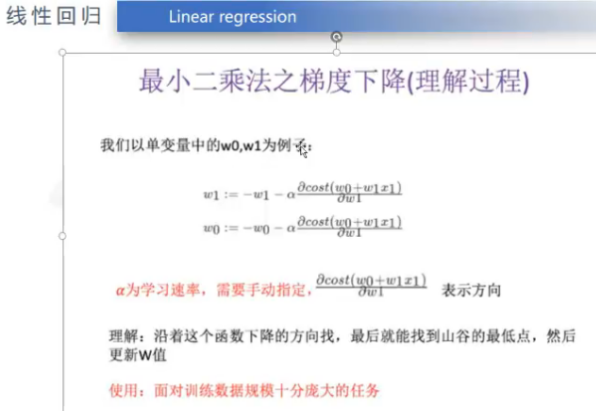
 梯度下降就是寻找最佳的权重w的方法之一。

 2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

中国从1971年开始全面开展了计划生育，使中国总和生育率很快从1970年的5.8降到1980年2.24，接近世代更替水平。此后，人口自然增长率很大程度上与经济的发展等各方面的因素相联系，与经济生活息息相关。影响中国人口自然增长率的因素有很多，如经济整体增长、居民消费水平、文化程度、人口分布，以及非农业与农业人口的比率等。

希望通过历史数据分析，对未来人口增长率进行预测。

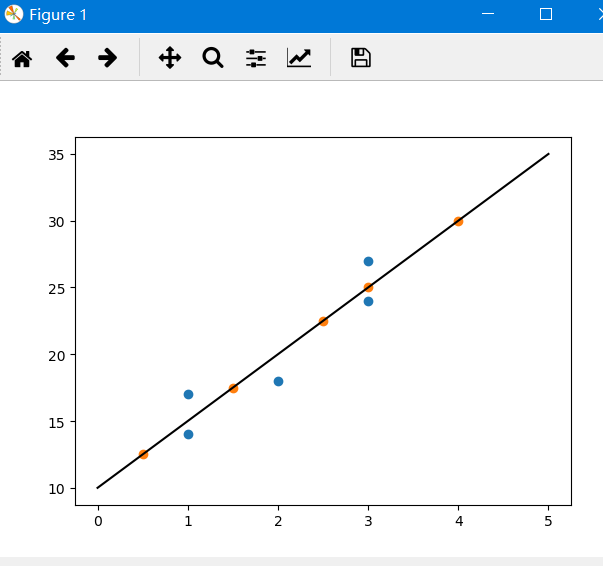
3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

import numpy as np
from matplotlib import pylab as pl

# 定义训练数据
x = np.array([1,3,2,1,3])
y = np.array([14,24,18,17,27])

# 回归方程求取函数
def fit(x,y):
    if len(x) != len(y):
        return
    numerator = 0.0
    denominator = 0.0
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    for i in range(len(x)):
        numerator += (x[i]-x_mean)*(y[i]-y_mean)
        denominator += np.square((x[i]-x_mean))
    print('numerator:',numerator,'denominator:',denominator)
    b0 = numerator/denominator
    b1 = y_mean - b0*x_mean
    return b0,b1

# 定义预测函数
def predit(x,b0,b1):
    return b0*x + b1

# 求取回归方程
b0,b1 = fit(x,y)
print('Line is:y = %2.0fx + %2.0f'%(b0,b1))

# 预测
x_test = np.array([0.5,1.5,2.5,3,4])
y_test = np.zeros((1,len(x_test)))
for i in range(len(x_test)):
    y_test[0][i] = predit(x_test[i],b0,b1)

# 绘制图像
xx = np.linspace(0, 5)
yy = b0*xx + b1
pl.plot(xx,yy,'k-')
pl.scatter(x,y,cmap=pl.cm.Paired)
pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
pl.show()