二叉树数据结构及其遍历

一、二叉树的定义及相关知识点

　　1.定义：再计算机科学中，二叉树是每个结点最多有两个子树的树结构，且二叉树的子树有左右之分，顺序不能任意颠倒；

　　2.性质：

　　　　a.如果二叉树的根节点层次从0开始，那么第i层树的节点为 2ⁱ 个节点；

　　　　b.高度为k的一个二叉树，那么它的结点node至多有2^k-1个结点（k>=1，这里注意了有些博客以及维基百科中是k>=0，从0开始的，所以高度为K的二叉树节点之多为2^(k+1)-1个结点）；

　　　　c.对任何一棵二叉树，如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1（这一条不太理解，待学习）。

　　3.完美二叉树（满二叉树）：深度为K（K>=1）的一个二叉树，其结点有2^k-1个结点，则该二叉树为完美二叉树；

　　　　

　　4.完全二叉树：从根结点到倒数第二层，满足完美二叉树（满二叉树），最后一层可以不完全填充，但是必须按照从左到右的顺序，其叶子结点都靠左对齐;

　　

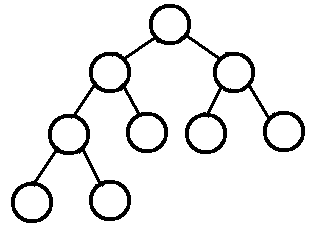
　　5.完满二叉树

　　未完待续......

二、二叉树的遍历

<?php
class Node{
    public $value = Null;
    public $child_left = Null;
    public $child_right = Null;

    function __construct($value)
    {
        if(!is_null($value) || !empty($value))
            $this->value = $value;
    }

    /***
     * 创建$this->>value的左右子树节点
     * @param $left
     * @param $right
     *
     */
    public function createNodeLrChild(Node $left=Null, Node $right=Null)
    {
        if(is_null($this->value) || empty($this->value))
            return false;
        if(!is_null($left) && !empty($left))
            $this->child_left = $left;
        if(!is_null($right) && !empty($right))
            $this->child_right = $right;
    }
}

final class Ergodic{
    /***
     * 先序遍历：先从根节点、再左子树、再右子树；在遍历左右子树的时候，仍然需要先从根节点开始遍历，再遍历左子树，再遍历右子树
     * @param $root
     */
    public static function preOrder($root)
    {
        #  定义一个栈
        $stack = array();
        array_push($stack, $root);

        # 循环取出节点的左右子树并压入栈中，再取出
        while(!empty($stack))
        {
            // 弹出一个节点，并输出节点的值
            $center_order = array_pop($stack);
            echo $center_order->value.' ';

            // 取出左右子树节点，并压去栈中（注意顺序：先序遍历是根节点、左子树、右子树；所以应该先压入右子树节点，先进后出）
            if(!empty($center_order->child_right) && !is_null($center_order->child_right))
                array_push($stack, $center_order->child_right);
            if(!empty($center_order->child_left) && !is_null($center_order->child_left))
                array_push($stack, $center_order->child_left);
        }
    }

    /***
     * 中序遍历：先左子树、再根节点、再右子树；
     * @param $root
     */
    public static function midOrder($root)
    {
        $stack = array();
        $center_order = $root;
        while(!empty($stack) || !empty($center_order) || $center_order !=null)
        {
            while($center_order !=null)
            {
                var_dump($center_order); // 输出该信息，有助于理解遍历的过程
                array_push($stack, $center_order);
                $center_order = $center_order->child_left; // 一直查找节点的左子树节点（是否有值，如果没有，则退出循环）
            }

            $center_order = array_pop($stack); // 然后弹出该节点的对象，获取该节点的值
            echo $center_order->value.' ';// 输出该值
            $center_order = $center_order->child_right; // 然后再获取该节点的右子树的值(看看是否存在左子树等)
        }
    }

    /***
     * 后序遍历
     * @param $roots
     */
    public static function endOrder($root)
    {
        $stack = array();
        $visit_stack = array();
        array_push($stack, $root);
        while(!empty($stack))
        {
            $center_order = array_pop($stack);
            array_push($visit_stack, $center_order);
            if($center_order->child_left != null)
                array_push($stack, $center_order->child_left);
            if($center_order->child_right != null)
                array_push($stack, $center_order->child_right);
        }

        while(!empty($visit_stack))
        {
            $center_order = array_pop($visit_stack);
            echo $center_order->value.' ';
        }
    }
}

# 创建二叉树数据结构
$a = new Node('A');
$b = new Node('B');
$c = new Node('C');
$d = new Node('D');
$e = new Node('E');
$f = new Node('F');
$g = new Node('G');
$h = new Node('H');
$i = new Node('I');

# 添加节点的左右子节点
$a->createNodeLrChild($b, $c);
$b->createNodeLrChild($d, $g);
$c->createNodeLrChild($e, $f);
$d->createNodeLrChild($h, $i);

# 先序遍历
//Ergodic::preOrder($a);
//echo "\n";
//Ergodic::midOrder($a);
//echo "\n";
//Ergodic::endOrder($a);