c 浮点数
2017-08-10 18:49 ZengGW 阅读(861) 评论(0) 编辑 收藏 举报一、二进制小数
十进制小数: 12.3410 == 1 * 101 + 2 * 100 + 3 * 10-1 + 4 * 10-2 = 12(34/100)
(可能很多人还不知道怎么计算一个数的负幂,这里给大家一个方法:一个数的负的X次方等于这个数的X次方分之一,比如2-2 = 0.25 = 1/2*2 = 1/4,现在明白不?)
二进制小数:101.11 == 1 * 22 + 0 * 21 + 1 * 20 + 1 * 2-1 + 1 * 2-2 = 4 + 0 + 1 + 1/2 + 1/4 = 5(3/4)
从二进制小数可以看出点左边的位的权是2的正幂;而点右边的位是2的负幂
下图是数b的定义:

从该图中不难看出有两种情况:
a>. 把小数点向左移动一位的时候相当于这个数被除以2(比如:101.112 = 5.75 --- 往左移动一位 -->10.1112 = 1 * 22 + 0 * 21 + 1 * 2-1 + 1 * 2-2 +1 * 2-3 = 2 + 0 + 1/2 + 1/4 + 1/8 = 2(7/8) = 2.875,)
b>. 把小数点向右移动一位的时候相当于这个数被乘于2(比如:101.112 = 5.75 --- 往左移动一位 -->1011.12 = 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 +1 * 2-1 = 8 + 0 + 2 + 1 + 1/2 = 11(1/2) = 11.5)
注意:
a>. 比如0.1,11112这样的数,刚好小于1,这样的数表示(63/64),我们使用科学计数法来表示:1.0-€
b>. 比如1/3、5/7这样的数,就是二进制小数所表单不了的,二进制小数表示法只能表示那些能够被写成x * 2y 的数
下面是一些题目,咱们借着题目分析一下(这个题目是深入理解计算机系统第三版的练习题):

疑问:
1.如何知道二进制小数部分有几位小数? 答:看分母,将分母换算成二进制,得到n位二进制数再减1(8 = 1000 = 4-1 = 3),比如1/8 = 0.001、1/2 = 0.1、1/16 = 0.0001
2.分子换算成小数部分后从小数点往右 位权越大还是越小? 答:从小数点往右二进制位的权越来越小,比如:1/16 =0.0001(有人计算出来是0.1000,这样是错的,这样的结果就是8/16 = 1/2 = 0.5 = 5 * 10-1 = 5/10 = )-------->这里涉及到十进制小数转二进制小数的问题,就是用小数去乘以2,不断的取整数:0.5 * 2 = 1.0 取1,小数部分就是1,结果就是0.1,一直乘以2,知道结果为1.0位置
a>. 3/8,首先分子比分母小,结果小于1;分母为8抓成二进制1000,小数部分则是n-1 = 3,分子部分011(是从右往左的),结果就是0.011;十进制:0.(1 * 2^-2 + 1 * 2^-3) = 3/8 = 0.375
b>. 23/16,首先分子大于分母,结果大于1,先计算整数部分为1,剩余为7/16,确定几位小数16 = 10000,小数位n-1 = 4,分子转成4位二进制 = 0111,结果就是1.0111;十进制:1 * 2^0 + 1 * 2^-2 + 1 * 2^-3 + 1 * 2^-4 = 1 + 0.25 + 0.125 + 0.0625 = 1.4375
c>. 10.1101,逆向运算 1 * 2^1 + 1 * 2^-1 + 1 * 2^-2 + 1 * 2^-4 = 2 + 1/2 + 1/4 + 1/16 = 2 + 13/16 = 45/16;十进制:2.8125
d>. 1.011 === 1 * 2^1 + 1 * 2^-2 + 1 * 2^-3 = 1 + 4/8 + 1/8 = 13/8 = 1.625
e>. 5.375 首先整数部分是5 = 101,小数部分是0.375,按照十进制小数转二进制小数,不断乘2,取整数(011),小数部分是011,结果就是101.011;小数值:5(3/8) = 43/8
f>.3.0625 首先整数部分是3 = 11,小数部分0.0625 = 0001,结果就是11.0001;小数值:3(1/16) = 49/16
二、IEEE浮点表示
IEEE浮点标准(表示一个数):V = (-1)s * M * 2E (不太理解)
介绍:
符号(s):决定数是负数(s == 1)还是整数(s == 0),而对于数值0的符号位解释作为特殊情况处理
有效数(M):它是一个二进制小数,它的范围在1~2-€或者0~1-€之间
指数(E):2的幂(正负都有可能),它的作用是对浮点数加权
浮点数的位分为三个域,编码值:
符号位(s):决定正负
尾数(M):一个二进制小数
阶码(E):对浮点数加权
存储一个浮点数(s正负号、exp指数E,frac小数部分):
对于单精度浮点格式(32位):

对于双精度浮点格式(64位):

根据阶码(E)字段的值不同我们可以分为四类浮点数:
a>. 规格化浮点数:

规格化浮点数:阶码值E = e - bias(2k-1 -1),bias在单精度情况下是127,双精度情况下是1023,因此单精度下E的值为[-126~+127],在双精度下E的值为[-1022~+1023];对于小数字段frac,f =0. fn-1fn-2.....f0,而位数M = f +1;在这里我们将浮点数的首位默认为1,所以没有显示的存储在存储器中,为什么能这样呢?因为我们可以通过调整阶码值E,使小数部分二进制的值落在1~2之间,获得额外的精度为
例如:0.10111,存储的话小数部分的二进制位是5位,存储就是000...10111,但是浮点数首位默认为1之后,我们小数部分存4位就可以了,1.0111 * 2-1 (why??前面咱们提到过,二进制小数,小数点往左移动一位就是除以2,往右移动就是乘以2,在这里我们往右移动了一位,结果就是1.0111,那么我们还原回去保持值不变就必须除以2,也就是*1/2)
表示范围:单精度下[-2^127,2^127],双精度下[-2^1023,2^1023],那么规范化的绝对值是大于 2 ^ (-126) 或 2 ^ (-1022) 的数字
示例1:0.25,先转成二进制小数0.01,那么根据规范化的属性转换一种形式,小数点往右移动2位 (0.01 * 2^2) * 2^-2 = 1.0 * 2^-2,根据阶码值计算E = -2 + 127 = 125,二进制小数部分全部都是0,那么最后的结果就是0 0111 1101 0000 0000 0000 0000 0000 000
示例2:1.5,转成二进制1.1,规格化默认首位为1,先忽略,0.1 * 2^0,那么阶码E = 127 + 0 = 127 = 01111111,小数部分1,后边补齐0即可,结果就是0 0111 1111 1000 0000 0000 0000 0000 000
b>. 非规格化浮点数:

非规格化浮点数:定义阶码E = 1 - bias (2k-1 -1),M = f = 0.fn-1 fn-2 fn-3 …… f2 f1 f0
表示范围:非规范化浮点数表示的则是小于 2 ^ (-126) 或 2 ^ (-1022) 的值
c>. 无穷大:

无穷大:frac部分二进制小数全为0
d>. NaN(Not a Number)

NaN:frac部分二进制小数不全为0
下边是几个文章的链接(写的特别好):
http://blog.csdn.net/hqin6/article/details/6701109
http://www.atjiang.com/CSAPP3-2.4_floating_point/
https://yasicyu.com/newarticle/IEEE-754%E6%A0%87%E5%87%86%E4%B8%8E%E5%AE%9E%E7%8E%B0
下面是一些练习题,本人对这一部分不是很懂,所以记录一下面试题的分析过程:
IEEE浮点格式的5位浮点数表示,1位符号位、2个指数位(k=2)和2位小数,指数偏移量bias = 2k-1 - 1 = 1
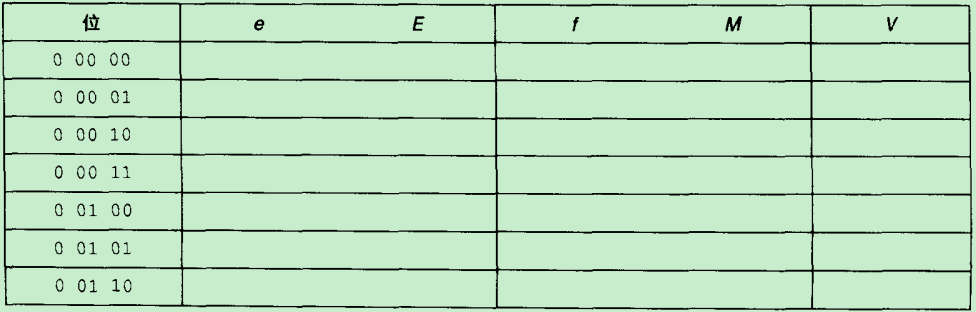

注意(0 00 00):
1.IEEE754浮点数表达式: V = M * 2e bias = 2k-1 - 1 = 1
2. 规格化数:E = e - Bias = e - 2k-1 - 1;M = f + 1
2.1 规格化数的范围:小数部分 0+1 = 1 ~ 1+3/4 = 7/4, V的范围 1 * 2^-1 = 1/2 ~ 2 * 7/4 = 14/4
3.非规格化数:E = 1 - Bias = 1 - 2k-1 - 1;f = M
3.1.非规格化数的范围:小数部分 0 ~ 3/4;阶码值为0,V的范围0 ~ 3/4
开始做题:
a>. 0 00 00: e = 0; E = 1-bias = 0; f = 0; M = 0; V = 0;
b>. 0 00 01: e = 0; E = 0; f = 1/4; M = f = 1/4; V = 1/4 * 2^0 = 1/4
c>. 0 00 10: e = 0; E = 0; f = 2/4; M = f = 2/4; V = 2/4 * 2^0 = 2/4
d>. 0 00 11; e = 0; E = 0; f = 3/4; M = f = 3/4; V = 3/4 * 2^0 = 3/4
e>. 0 01 00(这个就不再是非规格化数了,非规格化数的特点是阶码值全为0,这个符合规格化数):e = 1; E = e - Bias = 1 - 1 = 0; f = 0; M = f + 1 = 4/4; V = 2^0 * 4/4 = 4/4
f>. 0 01 01: e = 1; E = 0; f = 1/4; M = f + 1 = 5/4; V = 2^0 * 5/4 = 5/4
g>. 0 01 10: e = 1; E = 0; f = 2/4; M = f + 1 = 6/4; V = 2^0 * 6/4 = 6/4
h>. 0 01 11: e = 1; E = 0; f = 3/4; M = f + 1 = 7/4; V = 2^0 * 7/4 = 7/4
i>. 0 10 00: e = 2; E = 1; f = 0; M = f + 1 = 4/4; V = 2^1 * 4/4 = 8/4
j>. 0 10 01: e = 2; E = 1; f = 1/4; M = f +1 = 5/4; V = 2^1 * 5/4 = 10/4
k>. 0 10 10: e = 2; E = 1; f = 2/4; M = f +1 = 6/4; V = 2^1 * 6/4 = 12/4
l>. 0 10 11: e = 2; E = 1; f = 3/4; M = f + 1 = 7/4; V = 2^1 * 7/4 = 14/4
m>. 0 11 00 :这种情况就是无穷大的情况,因为阶码值全是1,小数部分全是0
n>. 0 11 01: 这种情况就是NaN了,因为阶码值全是1,而小数部分不全是0(e = 3; E = 2; f = 1/4; M = f + 1 = 5/4; V = 2^2 * 5/4 = 20/4 > 14/4)
三、浮点数舍入
浮点数舍入有四种方法,默认的舍入方法:向偶数舍入(round-to-even),也被称为向最接近的值舍入;其他三种方法产生的实际值的确界;
向偶数舍入:它试图找到最接近的值,采用的方法是将数字向上或者向下舍入,使得结果的最低有效位是偶数
比如:1.5RMB、2.5RMB想偶数舍入的结果都是2RMB
向零舍入:正数向下舍入,负数向上舍入,|x^| <= |x|
向下舍入:把正数和负数都向下舍入,x- < x
向上舍入:吧正数和负数都向上舍入,x+ > x
四、浮点数运算
浮点数不具有结合性
对于任何x,都有NaN + x = NaN
浮点数满足单调性熟属性:a>=b ,对于任何a,b的值,除了x不等于NaN,都有x + a >= x + b
五、浮点数
int、float、double三个类型相互转换:
a>. int转float,数值不会溢出,可能会被舍去
b>. int、float转double,因为double的范围更大,也有更高的位数(更多的有效位),能够保留精确的值
c>.double转float,从大范围转成小范围,所以值可能会溢出成+∞或-∞,由于精度较小,可能会被舍去
d>. double、float转int值将会向0截断,比如1.9999将会等于1,-1.99999将会等于-1


