c 整数运算

一、无符号加法（形式的模运算，无符号加法等价于计算模2^w 的和）

　　示例：非负数 x 和 y

　　位数： w(8位机)

　　范围： 0 <= x,y <= 2^w -1 

　　结果：0 <= x+y <= (2^w -1 + 2^w -1)  ====>  0 <= x+y <= 2^{w +1}-2  

　　比如：200 + 100 = 300 (2^w -1 <= 300 <=  2^{w +1}-2 )  ====> 300 mod 2^w(256) = 44

　　过程：300转换成二进制：100101100，但是咱们是8位机，我们从右往左数，左边的是高位，右边的是低位，把去高位舍去，保留8位：00101100（转换成10进制就是44）

　　那么这里就会出现一个很重要的概念：溢出？拿上边的示例来说明：当x + y > 2^w -1的时候，这个x+y的结果就会溢出，如图（整数加法和无符号加法之间的关系）：

　　

　　从这个图中我们可以分析一下，大概有两种情况（假设：w为4位 ）：

　　a. x + y < 2^w 它的结果的w+1位表示中的最高位会等于0，就算丢弃了最高位也不会改变值得大小，可能大家会很疑惑这事什么意思？

　　　　比如： 6+5 = 12 < 2⁴(16)，那么12的4位二进制表示 1100，w+1位的表示为01100，这就是上边说的w+1位表示中的最高位会等于0，就算把这个最高位去掉，结果变成4位1100，还是12，值不变

　　b. 2^w < x + y < 2^w+1 它的结果的w+1位表示中最高位会等于1，因此如果咱们把最高位丢弃了，它就相当于减去了2^w ？？？？？

　　　　比如：5+16 = 21，那么2^w(16) < 21 < 2^w+1(32)，21的二进制是 10101,最高位是1，那么去掉最高位的话结果就是0101（5），结果 x + y - 2^w，从上图可以看出 0 < x + y - 2^w < 2^w+1 - 2^w = 2^w ,结果就在0~2^w 中，刚好x和y的和，然后再模2^w 的结果

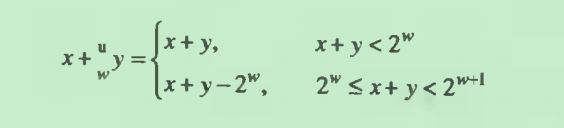　　，该图就是对上边两种情况最好的表示

　　那么咱们说一个算术溢出，是指完整的正数结果不能放到该数据类型的字长限制中去，就像上边的例子一样，w位4位，最大值为16，计算出一个21，那么这就是算术溢出，21不能放到4位长度类型里边去，

　　如何判断是否发生了溢出呢？？

　　　　比如： s = x + y；w=4， 0 <= x，y <= 2^w

　　　　（1）.当x + y >= x的时候，s就没有溢出，可以肯定s >= x；比如 1+13 = 14 < 2^w 没有产生溢出，结果是14，那么 1+13 >= x 

　　　　（2）.当s确实溢出了，那么公式就是s = x + y - 2^w ,比如 1+15 = 16 >= 2^w ,产生了溢出，结果当然是0了，那么 s < x，就产生了溢出

　　加法逆元（必须满足 -x + x = 0）：

　　　　a. x = 0，那么它的加法逆元就是0

　　　　b. x > 0，那么它的加法逆元就是 2^w - x，这是为什么呢？ 根据逆元运算 -x + x = 0  =====> x + 2^w - x = 2^w == 2^w 溢出了，结果就是0

　　　　

二、二进制补码加法

　　先来两张图有符号转无符号和无符号转有符号的图

　　1.有符号转无符号（T2U_w = x_w-12^W + X;）

　　

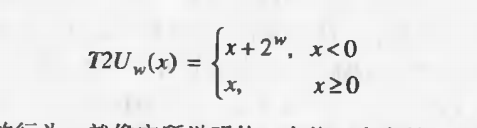
　　2.无符号转有符号（U2T_w = -x_w-12^W + X;）

　　

　　范围：-2^w-1 <= x,y <= 2^w-1 

　　补码加法： x + y = U2T_W(T2U_W(x) + T2U_w(y))  ====> 也就是　先是x和y的补码先相加，然后再转成有符号的数

　　　　　　　x + y = U2T_w[(-x_w-12^W + X + -y_w-12^W + y) mod 2^w] = [(x + y) mod 2^w]（这里可能大家会很奇怪，其实-x_w-12^W和-y_w-12^W就类似于求模取余是一样的）

　　这里会出现四种情况：负溢出、正常、正常、正溢出

　　1.负溢出：结果z，-2^w <= z < -2^w-1, 根据有符号转无符号的规则，z < 0, z¹ = z + 2^W，那么z的无符号数 0 <= z¹ < 2^w-1 ,我们看到了z¹ 在满足 z³ = z¹ 的范围之内（这里是补码相加，根据无符号转有符号的规则，z < 2^w-1,所以相等），那么这种情况就是负溢出，我们将两个负数x和y相加（我们能得到z < 2^w-1，根据无符号转有符号的规则，z保持不变） ,得到一个非负数的结果 z³ = x + y + 2^w；

　　2.正常：结果z，-2^w-1 <= z < 0，根据有符号转无符号的规则，z < 0, z¹ = z + 2^W，那么z的无符号数 2^w-1 <= z¹ < 2^w，z¹ = z³ - 2^w（因为根据无符号转有符号的规则，z >= 2^w-1，则z¹的有符号值必须减去2^w才行）,而z¹ = z + 2^W ，那么z³ = z¹ - 2^w =  z + 2^W - 2^w = z

　　3.正常：结果z，0 <= z < 2^w-1 ,根据有符号转无符号的规则，z > 0，z¹ = z，得到0 <= z < 2^w-1 ，根据无符号转有符号的规则，z <  2^w-1，所以z保持不变， z = x + y；

　　4.正溢出： 2^w-1 <= z <  2^w ，z > 0，z¹ = z，但是由于z的范围在2^w-1以上，根据无符号转有符号的规则，z³ = z¹ - 2^w， z³ = x + y - 2^w这种情况就是正溢出的情况，得到的结果将是负数，如下图：

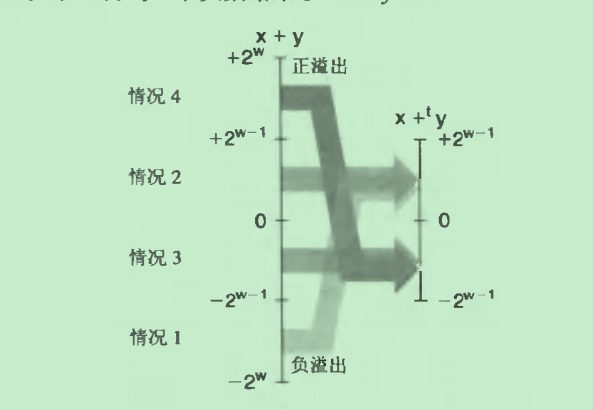　　从图中可以看出当结果在z < -2^w-1的时候是负溢出，在-2^w-1 <= z < 2^w-1 为正常，在2^w-1+1 <= z 为正溢出

　　下面是公式：

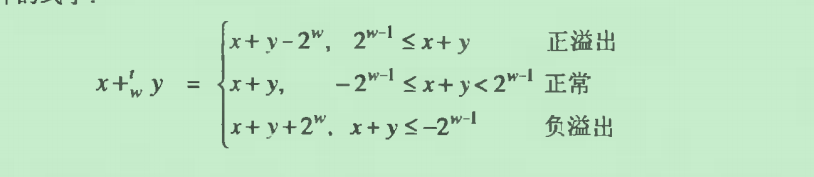　　不难看出正负溢出

 三、二进制补码的非

　　在范围-2^w-1 <= x < 2^w-1中的每个数字x都有二进制补码加法的加法逆元的（w=4，那范围就是-8 <= x < 8）；

　　1. 当x 不等于 -2^w-1 的时候，它的加法逆元是 -x ，-x 的范围 -2^w-1 < -x < 2^w-1 ，而 -x + x = 0

　　　　比如： -6 它的加法逆元就是 6，-6 + 6 = 0

　　　　过程：-6 的二进制补码 （0110 ---> 1001+1）1010 = 10，那么10 + 6 = 16, 2^w-1 <= 16 ，属于正溢出，根据正溢出的规则，x + y - 2^w = 16 - 16 = 0;

　　2. 当x = -2^w-1 = TMin_w ，那么-x = 2^w-1 ,则-x + x =  -2^w-1 + 2^w-1 = 0；

　　　　比如：-8 它的加法逆元就是8， -8 + 8 = 0

　　　　过程：-8的二进制补码（1000 ---> 0111+1 = 1000）,而8的二进制是10000，那么 8 + 8 = 16(10000，保留4位0000)，根据补码运算规则，属于正溢出，x + y - 2^w = 16 - 16 = 0;

　　如图（二进制补码的非运算）：

　　　　从这里可以看出，当x = -2^w-1 的时候，其实x的加法逆元就等于它本身，当x大于有符号最小值时，加法逆元是它2^w - x

　　通过上边的分析，其实大家应该能发现规律，那就是二进制补码的非可以使用另一种方式：先使用按位取反运算，然后再将结果+1，在c中公式就是 ^~x + 1（比如4位机：15的二进制1111，先取反再加一0000+1 = 0001 = 1），那么15 的二进制补码的非就是1

四、无符号乘法

　　范围 0 <= x,y < 2^w-1 内的正数

　　乘积的范围： 0~(2^w-1)²  = 2^2w - 2^w+1+1

　　如图：

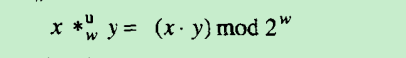　　　　其实无符号乘法等价于计算模2^w 的乘法，比如：w=4， 3*8 = 24 mod 16 = 8

五、二进制补码乘法

　　范围：-2^w-1 <= x,y <= 2^w-1 -1内的整数

　　乘积的范围： -2^w-1 * （-2^w-1 -1） = -2^2w-2 + 2^w+1 ~ -2^w-1 *-2^w-1  =  -2^2w-2

　　如图：

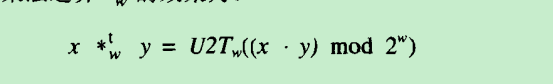　　　　这就是二进制补码乘法的运算效果，跟无符号乘法差不多，只不过最后要根据无符号转有符号而已

　　二进制补码乘法和无符号乘法，他们的乘法运算的位级表示其实是一样的，机器可以使用一种乘法指令来进行有符号和无符号整数的乘法

　　公式：x * y mod 2^w = [(x_w-12^W + X) * (y_w-12^W + y)] mod 2^w 

　　　　　　　　　　　= [x * y + (x_w-1y + y_w-1x)2^w + x_w-1 y_w-12^2w]  mod 2^w 

　　　　　　　　　　　= (x * y)  mod 2^w 

　　从这个公式可以看出，无符号和有符号整数乘法位级表示是一样的

　　下面来做一个练习题（一个一个来分析）：

　　

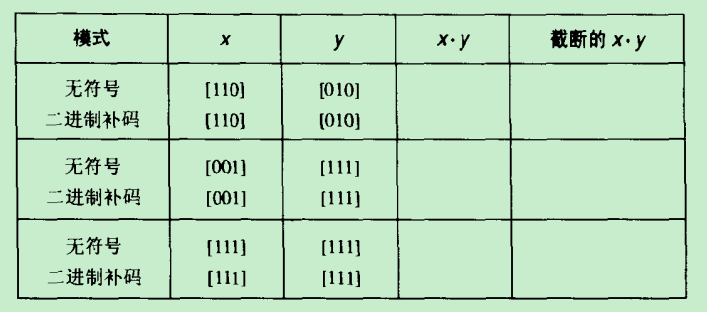
　　a>. 无符号： 110（6） * 010（2） = 12（001100） ==> 100(4)

　　　  补码：110（^~(110 - 1) = 010 = -2） * 010（2） = -4（000100-> 111011+1 = 111100） ==> 100(4)

　　b>.无符号：001（1） * 111（7） = 7（000111）==>111(7)

　　　  补码：001（1）* 111（^~（111-1） = 001 = -1） = -1（111111） ===> 111(7)

　　c>.无符号：111（7） * 111（7） = 49（110001） ===> 001(1)

　　　  补码：111（^~（111-1） = 001 = -1） * 111（^~（111-1） = 001 = -1） = 1（000001）===> 001（1）

六、乘以2的幂

　　大多数机器上边整数乘法相当的慢，其他的运算就比较的快了，相差差不多12倍，因此编译器使用的一项重要的优化：用移动（左移）和加法运算的组合代替乘以常数因子的乘法，如图：

　　从图中可以看出咱们位移运算，左移k位就是往右边添加k个0，

　　当然了如果位移的k大于w的话，那么结果肯定是保留w位，多余的截取掉了（是高位截取）,截取后的默认是有符号的数字，根据规则这个位向量的值为x2^k mod 2^w ,因此对于无符号变量x，c的表达式 x << k == x * pwr2k = x * 2^k (pwr2k等价 2^k)

　　比如：2 << 3 = 2 * 2³ = 16

七、除以2的幂

　　大多数机器上边整数除法相当的慢，比整数乘法更慢，相差差不多30倍，除以2的幂也可以使用位移来实现：使用右移，对于二进制补码数和无符号数，分别使用算术位移和逻辑位移，整数除法总是舍入到0

　　示例1（无符号数，使用逻辑右移来运算）：x = [x_w-1,x_w-2......x₀]（原始值）        x¹ =  [x_w-1,x_w-2......x_k]（位移k位后的值）   　　x² =  [x_k-1,x_k-2......x₀]（右移舍去的位）

　　位数：w位，移动k位(0<= k < w)

　　公式： x¹ = x/2^k

　　证明过程：x = x_i2ⁱ，x¹ = x_i-k2^i-k，x² = x_k2^k  == 根据x¹ = x/2^k ==> x = 2^kx¹ + x² 

　　　　　　0 < x² <= 2^k-1（2^k），那么x² / 2^k = 0（可能大家不太明白为什么等于0，因为无符号数除法，使用的是右移和逻辑移动，那么比如1/1 = 0，为什么呢？因为1的二进制位0001，往右移动一位为0000，结果就为0），就有x/2^k = x¹ + x²/2^k =  = x¹

　　结果：对于位向量[x_w-1,x_w-2......x₀]，使用逻辑右移k位会得到一个新的位向量[0,........0,x_w-1,x_w-2......x_k]，x¹其实就是将一个无符号的数进行逻辑右移k位，等价于除以2^k ,所以c表达式 x >> k,等价于x/pwr2k,pwr2k就等于2^k

　　示例2（二进制补码，使用算术右移来运算）:跟上边无符号的推理过程基本一样，只不过得到的结果不一样

　　结果：对于位向量[x_w-1,x_w-2......x₀]，使用算术右移k位，得到一个新的位向量：[x_w-1,x_w-1,x_w-1,x_w-2......xk]，它刚好是将[x_w-1,x_w-2......xk]从w-k位符号扩展到w位，这个移位的结果就是[x/y]的二进制补码表示

　　　　a. x > 0，这个移位的结果就是所期望的值

　　　　b. x < 0 和y > 0 ,整数的除法应该是x/y

　　　　c. 对于任何实数a， 被定义使得 a¹ - 1 < a <= a¹ ,整数除法应该将为负的的结果向上朝零舍入（比如：-5/2 = -2，-5的二进制补码表示0101=>1010+1 = 1011,往右移动一位==> 1101再有符号转无符号 1101-1 = ^~1100 = 0011 = -3）

　　　　e：设置“偏置”值来修正不合适的舍入，比如：整数x和y>0,[X/Y] = [(x+y-1)/y]，对于x<0，我们在右移之前先将x加上2^k -1,保障得到正确舍入的结果

　　　　d：（x < 0 ? （x + （1 << k）- 1）: x） >> k