51NOD 1277 字符串中的最大值（KMP）

》》点击进入原题测试《《

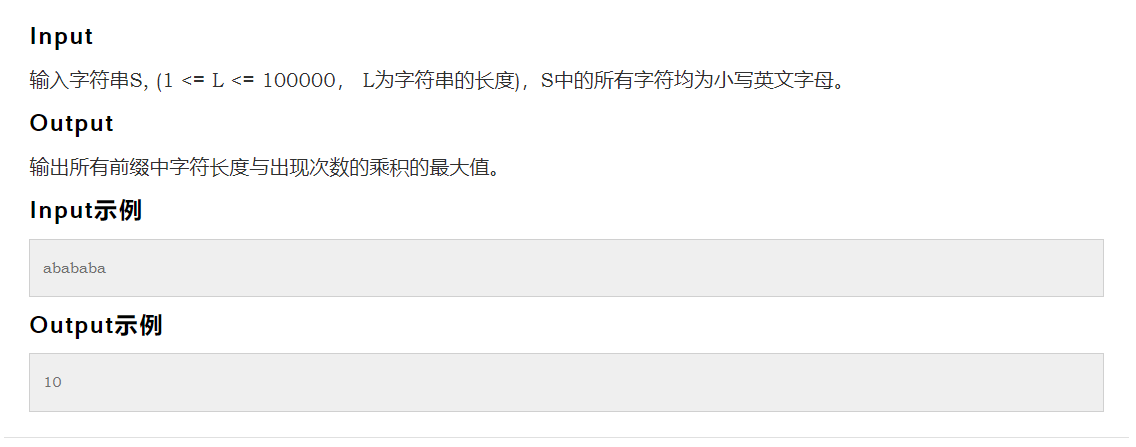
思路：用KMP优化的暴力写了一遍，超时！没有充分利用KMP中next数组的性质。

首先这个题是肯定要用到KMP算法的，然后会有一个next[]数组。

用一个数组来sum[i]表示长度为i的前缀的字符串有多少个，于是默认所有初始值为1；

然后倒着递推sum[next[i]]+=sum[i];原理的话自己找个样例手动模拟一下应该就清楚了，真的是很神奇的一个规律。

注意使用长整形，有个样例会溢出！

参照一下帖子 https://blog.csdn.net/largecub233/article/details/62039957

#include<cstdio>
#include<string>
#include<iostream>
using namespace std;
int ne[100010];
void cal_next(string str)
{
    ne[0] = -1;
    int k = -1;
    for (int i = 1; i < str.length(); i++){
        while (k != -1 && str[k + 1] != str[i])
            k = ne[k];

        if (str[k + 1] == str[i])k += 1;
        ne[i] = k;
    }
}
int kmp(string str, string str2)
{
    int k = -1, sum = 0;
    
    for (int i = 0; i < str.length(); i++){
        while (k>-1 && str[k + 1] != str[i])
            k = ne[k];
        if (str[k + 1] == str[i])
            k += 1;
        if (k == str2.length() - 1){
            sum++;
            i -= ne[k] + 1;
            k = -1;
        }
    }
    return sum;
}
int main()
{
    string a; cin >> a;
    int maxs = 0;
    cal_next(a);
    for (int i = 1; i <= a.length(); i++){
        string temp = a.substr(0, i);
        int ans = kmp(a, temp);
    //    cout << temp.length() << " " << ans << endl;
        if (ans*temp.length() > maxs)
            maxs = ans*temp.length();    
    }
    cout << maxs << endl;
    return 0;
}

#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define  ll long long
ll ne[100010], sum[100010];
void cal_next(string str)
{
    ne[0] = -1;
    int k = -1;
    for (int i = 1; i < str.length(); i++){
        while (k != -1 && str[k + 1] != str[i])
            k = ne[k];

        if (str[k + 1] == str[i])k += 1;
        ne[i] = k;
    }
}
int kmp(string str, string str2)
{
    int k = -1, sum = 0;
    
    for (int i = 0; i < str.length(); i++){
        while (k>-1 && str[k + 1] != str[i])
            k = ne[k];
        if (str[k + 1] == str[i])
            k += 1;
        if (k == str2.length() - 1){
            sum++;
            i -= ne[k] + 1;
            k = -1;
        }
    }
    return sum;
}
int main()
{
    string a; cin >> a;
    ll maxs = 0;
    for (int i = 0; i <= a.length(); i++)
        sum[i] = 1;
    
    cal_next(a);
    for (int i = a.length() - 1; i >=0; i--){
        maxs = max(maxs,(i+1)*sum[i+1]);
        sum[ne[i]+1] += sum[i+1];
    }
    cout << maxs << endl;
    return 0;
}