6-9 二叉树的遍历

6-9 二叉树的遍历（25 分）

本题要求给定二叉树的4种遍历。

函数接口定义：

void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

要求4个函数分别按照访问顺序打印出结点的内容，格式为一个空格跟着一个字符。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

BinTree CreatBinTree(); /* 实现细节忽略 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );

int main()
{
    BinTree BT = CreatBinTree();
    printf("Inorder:");    InorderTraversal(BT);    printf("\n");
    printf("Preorder:");   PreorderTraversal(BT);   printf("\n");
    printf("Postorder:");  PostorderTraversal(BT);  printf("\n");
    printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");
    return 0;
}
/* 你的代码将被嵌在这里 */

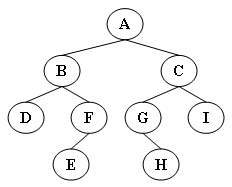
输出样例（对于图中给出的树）：

Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A
Levelorder: A B C D F G I E H
思路：原来C语言中没有STL🤯

void InorderTraversal(BinTree BT)
{
    if (BT == NULL)return;

    InorderTraversal(BT->Left);
    printf(" %c", BT->Data);
    InorderTraversal(BT->Right);

}
void PreorderTraversal(BinTree BT)
{
    if (BT == NULL)return;

    printf(" %c", BT->Data);
    PreorderTraversal(BT->Left);
    PreorderTraversal(BT->Right);
}
void PostorderTraversal(BinTree BT)
{
    if (BT == NULL)return;

    PostorderTraversal(BT->Left);
    PostorderTraversal(BT->Right);
    printf(" %c", BT->Data);
}
void LevelorderTraversal(BinTree BT)
{
    if (BT == NULL)return;
    
    BinTree binTree[100];
    int head = 0, last = 0;
    binTree[last++] = BT;
    
    while (head < last){
        BinTree temp = binTree[head++];
        printf(" %c", temp->Data);

        if (temp->Left)
            binTree[last++] = temp->Left;
        if (temp->Right)
            binTree[last++] = temp->Right;        
    }
}