51NOD 2370 奈芙莲的护符

》》这是原题传送门《《

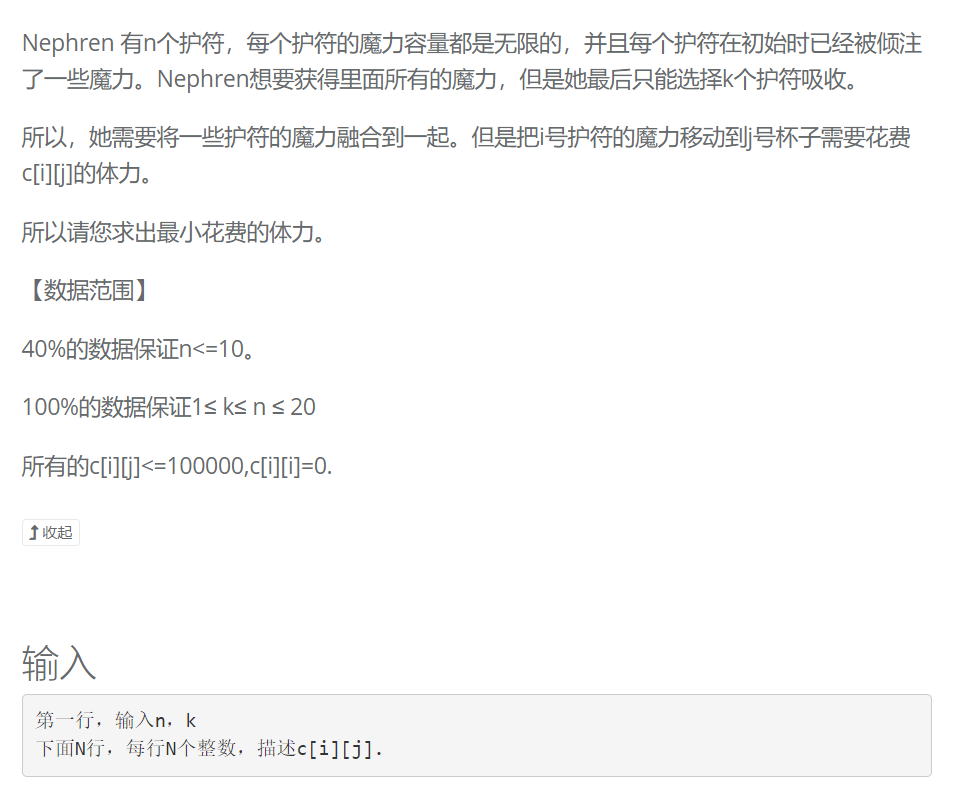
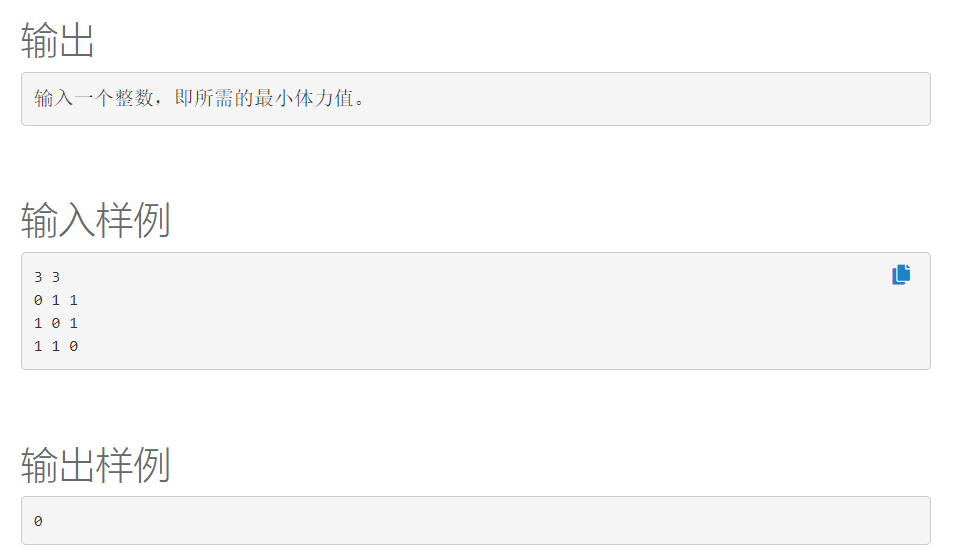
答案参考来自 http://www.cnblogs.com/sugewud/p/9822933.html

 思路：看到取值范围之后，仅有的思路还是暴力😔；上面链接的同学题解用的是状态压缩动态规划，emmmmm 我第一次接触，说点高兴的这个二进制我还是很熟悉的。

n的最大值为1048576，遍历到0的每一种状态，用1来表示魔力还在，0表示魔力已经转移；

从（1<<n)-1到0遍历，初始化dp[(1<<n)-1]=0;然后就能考虑到每一种从n个拥有魔力的护符到k个用友魔力的护符的所有情况。K以下就直接跳过，完美 /膜拜

 恬不知耻的贴一下别人代码🤫

#include<cstring>
#include<iostream>
#include<algorithm>
#define _ 0
#define ll long long
using namespace std;

const int maxm = (1 << 20) + 10;
const int maxn = 30;
int c[maxn][maxn], dp[maxm];
int num(int x){
    return !x ? 0 : 1 + num(x&(x - 1));
}
int main(){
    ios::sync_with_stdio(false);
    int n, k;
    while (cin >> n >> k){
        for (int i = 0; i < n; i++){
            for (int j = 0; j < n; j++){
                cin >> c[i][j];
            }
        }
        int ans = 1e9;
        memset(dp, 0x3f, sizeof dp);
        dp[(1 << n) - 1] = 0;
        for (int s = (1 << n) - 1; s >= 0; s--){
            if (num(s) < k)continue;
            for (int i = 0; i < n; i++)if (s&(1<<i))
            for (int j = 0; j < n; j++)if (!(s&(1 << j)))
                dp[s] = min(dp[s], dp[s ^ (1 << j)] + c[j][i]);
            if (num(s) == k)ans = min(ans, dp[s]);
        }
        cout << ans << endl;
    }
    return ~~(0 ^ _ ^ 0);
}