数和二叉树，查找算法总结

一.思维导图

二.重要概念笔记

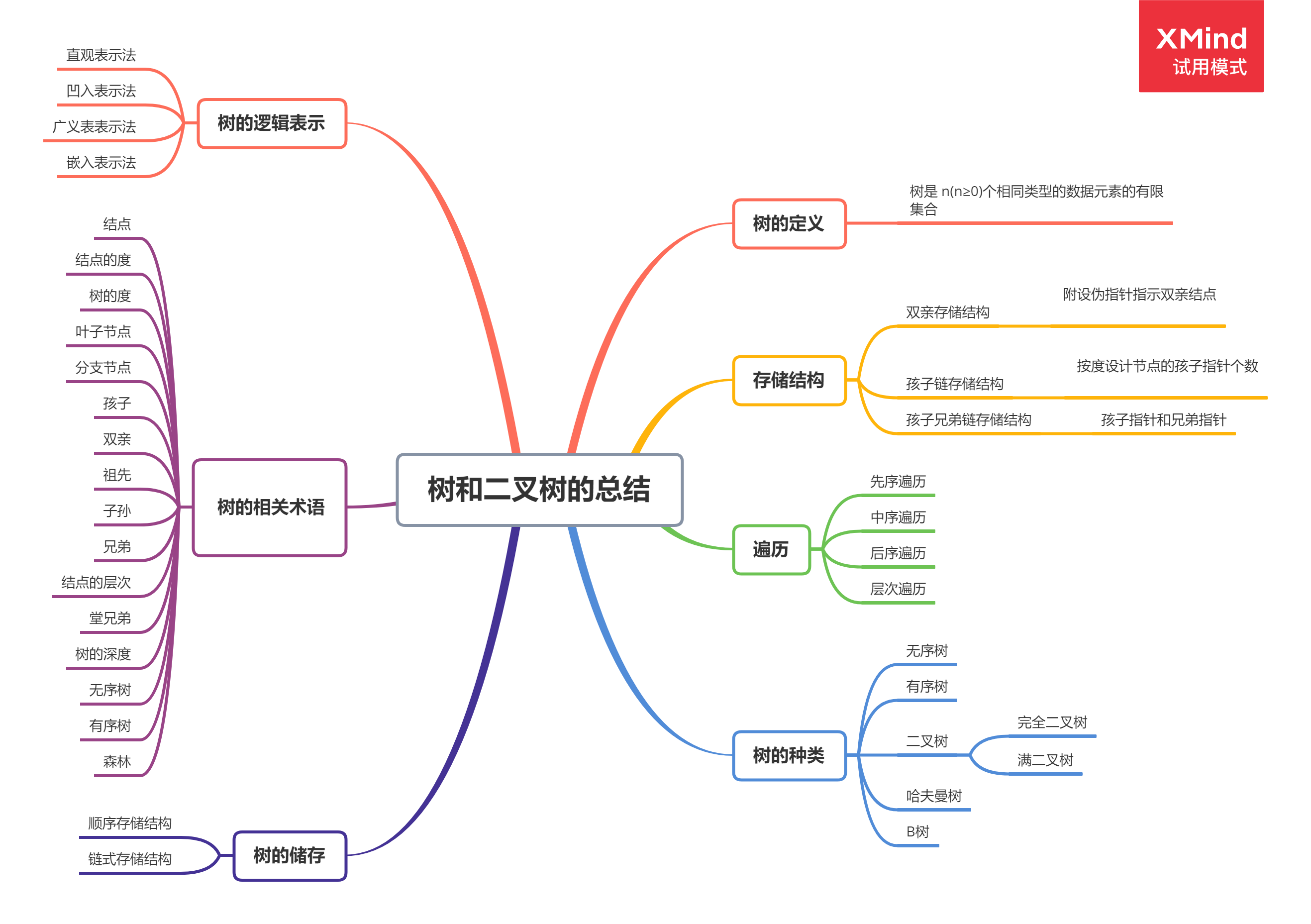
1.树

1.n=0 的树称为空树；对于n＞0的任意非空树T有：

-有且仅有一个特殊的结点称为树的根(Root)结点，根没有前驱结点
-若n＞1，则除根结点外，其余结点被分成了m(m＞0)个互不相交的集合T 1 ，T 2 ，…，T m ，其中每一个集合T i (1≤i≤m)本身又是一棵树。树T 1 ，T 2 ，…，T m
称为这棵树的子树

2.树的特点

-树的根结点没有前驱结点，除根结点之外的所有结点有且只有一个前驱结点
-树中的所有结点都可以有零个或多个后继结点

2.二叉树的遍历

1.前中后序遍历

以前序遍历为例

void preorder(node *root) {
		if( root == NULL)
			return; //到达空树,递归边界(前中后一样)
		printf("%d\n", root -> data); //访问根节点
		//访问左子树
		preorder(root -> lchild);
		//访问右子树
		preorder(root -> rchild);	
}

2.层序遍历

从树根自顶向下,且同层从左到右(需要用到队列)

void LayerOrder(node* root) {
		//存放node型变量的地址,可以直接对原元素进行修改
		queue<node*> q;
		q.push(root); //从根节点地址入队
		while( ! q.empty ( ) ){
				node* now = q.front(); //取出队首元素
				q.pop();
				printf("%d",now -> data); //访问队首元素
				if( now -> lchild ! = NULL)  {
						
						//升级版 
						//now -> lchild -> layer = now -> layer +1;
						//表示左孩子层号为右孩子加1
						q.push(now -> lchild) ; //左子树非空
				}
				if( now -> rchild ! = NULL)  { 
				        //升级版同上
						q.push(now -> rchild) ; //右子树非空
				}
		}
}

3.Eg: 已知先序和中序序列,要求构建一棵二叉树

node* create(int preL, int preR, int inL, int inR){
	// 先序序列区间[preL, preR], 中序序列区间[inL, inR]
	if(preL > preR) {
		return; //递归边界
	}
	node* root = new node;//新建一个节点
	root -> data = pre[preL]; //先序序列第一个值是根节点
    for(int i = inL; i <= inR; i++){
    	if(pre[preL] == in[i])
    		break; //在中序序列中找到与根节点的值相等的,确定分界线
    } 
    int leftin = i - inL;
    root -> lchild = create(preL+1, preL+leftin, inL, i-1);
    root -> rchild = create(preL+leftin+1, preR, i+1, inR);
    return root;
}

4.二叉排序树的构建，插入，查找与删除

InsertBST(T, key) {
    if (T为空) {
        创建T;
        T->data = key;
        T的左孩子 = T的右孩子 = 空;
        return;
    }
    else if (T->data = key)
        return;
    else if (key < T->data)
        InsertBST(T->lchild, key);
    else if (key > T->data)
        InsertBST(T->rchild, key);
}

int InsertBST(BTree& BT, int k) {
    if (BT == NULL) {
        BT = new BTNode;
        BT->data = k;
        BT->lchild = BT->rchild = NULL;
        return 1;
    }
    else if (BT->data == k) {
        return 0;
    }
    else if (k < BT->data) {
        return InsertBST(BT->lchild, k);
    }
    else
        return InsertBST(BT->rchild, k);
}
BTree SearchBST(BTree BT, int k) {
    if (BT == NULL || BT->data == k)
        return BT;
    if (k < BT->data)
        return SearchBST(BT->lchild, k);
    else
        return SearchBST(BT->rchild, k);
}
void DeleteBST(BTree & BT) {
    BTree q, s;
    if (BT->lchild == NULL) {
        q = BT;
        BT = BT->rchild;
        delete q;
    }
    else if (BT->rchild == NULL) {
        q = BT;
        BT = BT->lchild;
        delete q;
    }
    else {
        q = BT;
        s = BT->lchild;
        while (s->rchild) {
            q = s;
            s = s->rchild;
        }
        BT->data = s->data;
        if (q == BT)
            BT->lchild = s->lchild;
        else
            q->rchild = s->lchild;
        delete s;
    }
}

3.树的种类（概念）

1.无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树

2.有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树

3.二叉树：每个节点最多含有两个子树的树称为二叉树

-完全二叉树：对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；【倒数第一层不是倒数第二层的二倍，尚缺N个节点】
-满二叉树：对于上述的完全二叉树，如果去掉其第d层的所有节点，那么剩下的部分就构成一个满二叉树（此时该满二叉树的深度为d-1）；【倒数第一层是倒数第二层的二倍】

4.哈夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树

5.B树：【每一层数据大小有序】

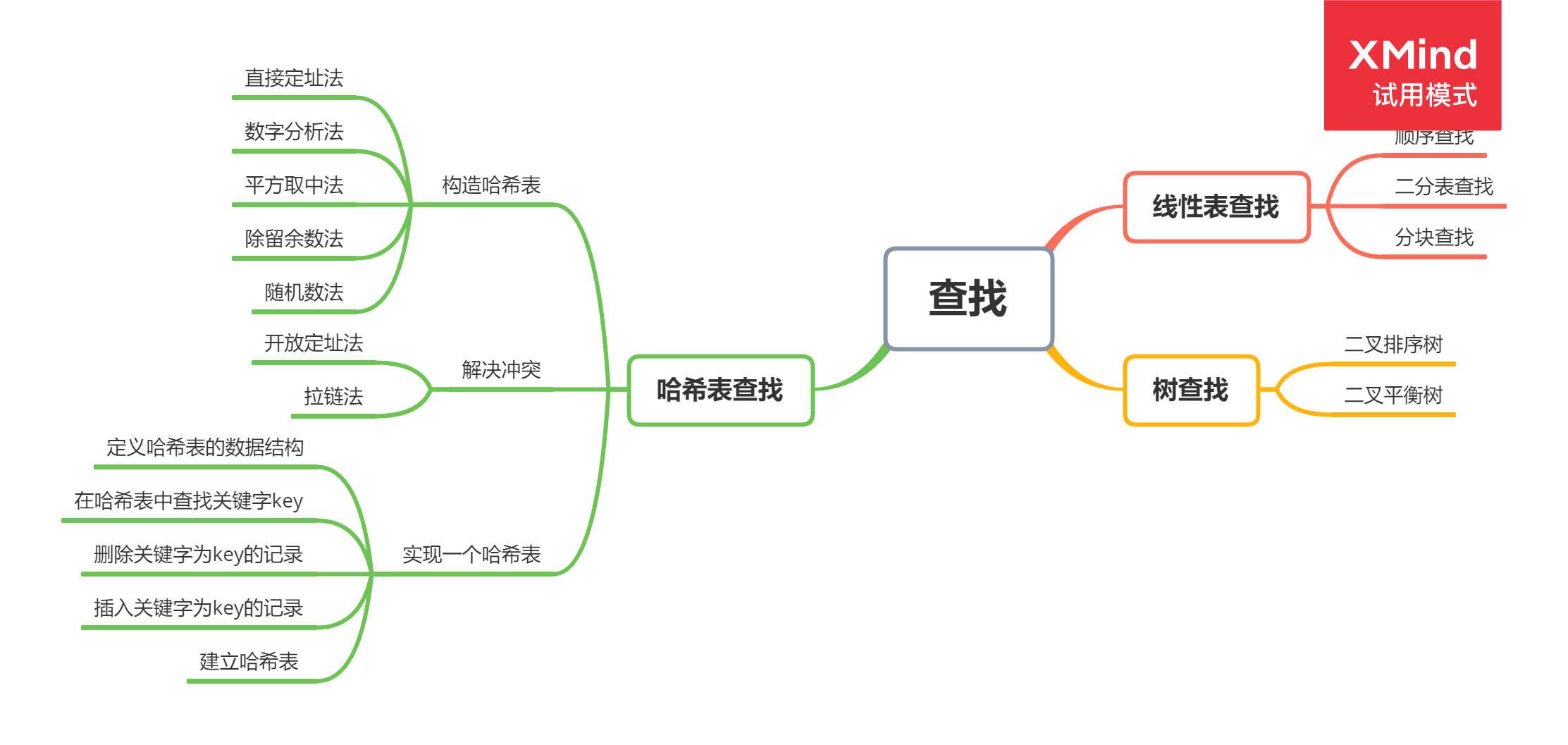
4.查找

1.二分法查找

void BinSearch(SeList r,int n,KeyType k)
{
	int low = 0, high = n - 1, mid;
	while (low <= high)
	{
		mid = (low + high) / 2;
		if (r[mid].key == k)
			return mid + 1;
		if (r[mid].key > k)
			high = mid - 1;
		else
			low = mid + 1;
	}
	return 0;
}

三.疑难问题

1.二叉树叶子结点带权路径长度和

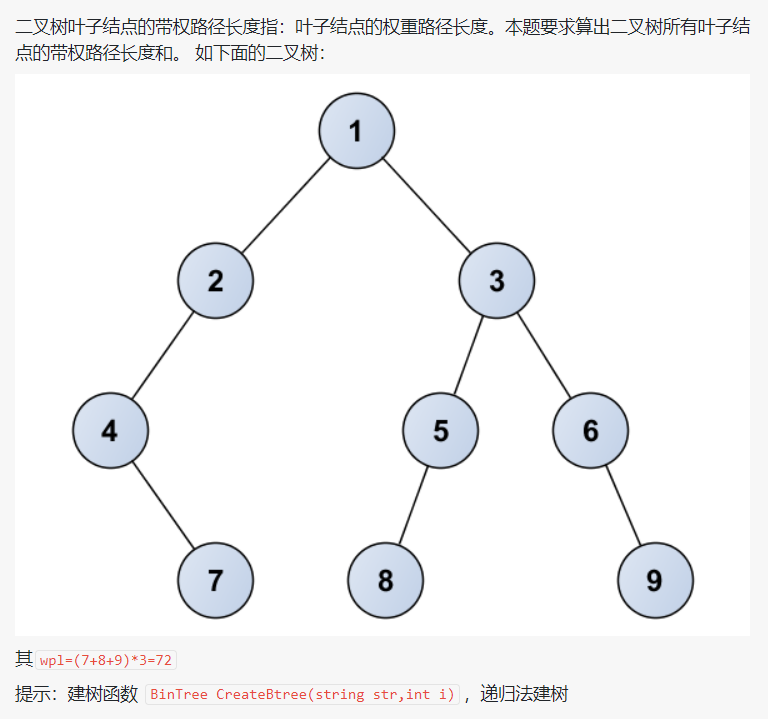
代码

#include<iostream>
#include<string>
using namespace std;
typedef struct BTNode {
    char data;
    struct BTNode *lchild, *rchild;
}BTNode, * BTree;
void CreateBtree(string S, BTree& BT, int i);//建树
int SumTree(BTree q, int i);//计算
int main() {
    BTree q;
    string s;
    cin>>s;
    CreateBtree(s, q,1);
    cout << SumTree(q, 0);
}
void CreateBtree(string S, BTree& BT, int i) {
    if (i >= S.size()) {
        BT = NULL;
        return;
    }
    if (S[i] == '#') {
        BT = NULL;
        return;
    }
    BT = new BTNode;
    BT->data = S[i];
    CreateBtree(S, BT->lchild, 2 * i);
    CreateBtree(S, BT->rchild, 2 * i + 1);
}
int SumTree(BTree q, int i) {
    if (q == NULL)return 0;
    if (q->lchild == NULL && q->rchild == NULL) {
        return (q->data-48) * i;
    }
    i++;
    return SumTree(q->lchild, i) + SumTree(q->rchild, i);
}