逻辑回归
1.1分类问题
在分类问题中,你要预测的变量 y 是离散的值,我们将学习一种叫做逻辑回归 (Logistic
Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。分类问
题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;之前我们
也谈到了肿瘤分类问题的例子,区别一个肿瘤是恶性的还是良性的。
1.2假说表示
sigmoid函数
因为线性回归模型预测的值超越[0,1]的范围,我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在 0 和 1 之间。


1.3判定边界

我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
1.4代价函数和梯度下降

因此,上述的Cost Function对于逻辑回归是不可行的,我们需要其他形式的Cost Function来保证逻辑回归的成本函数是凸函数。
我们跳过大量的数学推导,直接出结论了,我们找到了一个适合逻辑回归的代价函数:


当y=1时,hθ(x)趋向于1的cost值为0,反之cost则趋向于无穷大。当y=0时相反。这样就很好的惩罚了最后得结果。
简化代价函数

带入梯度下降公式得:

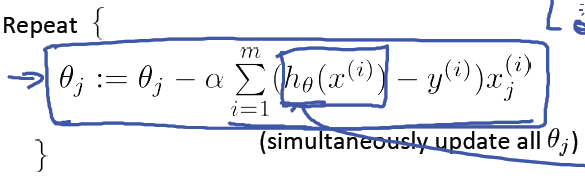
注意点:虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样,但是这里
的hθ(x)=g(θTx)与线性回归中不同,所以实际上是不一样的。另外,在运行梯度下降
算法之前,进行特征缩放依旧是非常必要的。

1.5多类别分类
用逻辑回归 (logistic regression)来解决多类别分类问
题,具体来说,我想通过一个叫做"一对多" (one-vs-all) 的分类算法。
举个例子:
假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里, 或者说可以自动地加上标签,那么,你也许需要一些不同的文件夹,或者不同的标签来完成 这件事,来区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好 的邮件,那么,我们就有了这样一个分类问题:其类别有四个,分别用 y=1、y=2、y=3、y=4 来代表。
为了能实现这样的转变,我们将多个类中的一个类标记为正向类(y=1),然后将其他
所有类都标记为负向类,这个模型记作hθ1(x)
。接着,类似地第我们选择另一个类标记为
正向类(y=2),再将其它类都标记为负向类,将这个模型记作
hθ2(x),依此类推。~~~概率论知识:当x和θ固定的情况下,求y=i得概率。

总之,我们已经把要做的做完了,现在要做的就是训练这个逻辑回归分类器:hθi(x),
其中 i 对应每一个可能的 y=i,最后,为了做出预测,我们给出输入一个新的 x 值,用这
个做预测。我们要做的就是在我们三个分类器里面输入 x,然后我们选择一个让
hθi(x)最大的i,即max hθi(x)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号