【数据结构与算法】2 - 2 矩阵的压缩存储
§2-2 矩阵的压缩存储
2-2.1 数组的存储结构
数组是 Java 语言所提供的已实现的存储结构。数组作为一个对象,其中元素被按顺序存放在堆的一片连续的存储空间中,可通过索引进行偏移寻址。堆中的元素需要通过栈中的引用变量访问,这种特性使得堆中的元素在存储空间中是零散的。这样,对于多维数组而言,其所有的元素并不一定都存放在一片连续的存储空间中。以二维数组 int[][] 为例,下图简要地解释了为什么二维数组(可推广至更高维数组)中的所有元素不会全部都存储在同一片连续存储空间内:
引用自 Stack Overflow: memory - Java: A two dimensional array is stored in column-major or row-major order? - Stack Overflow
而在 C++ 语言中,数组以行序优先的方式存储,一个数组中的所有元素必定按顺序连续存储在同一片存储空间中。
2-2.2 稀疏矩阵的定义及其压缩
当一个阶数较大的矩阵中的非零元素个数相对于矩阵元素的总个数非常小时,该矩阵称为稀疏矩阵(sparse matrix)。
同样地,当一个阶数较大的矩阵中不同值元素个数相对于矩阵中相同值的元素个数非常小时,这样的矩阵也称为稀疏矩阵。
稀疏矩阵的空间复杂度较大,而实际存储的有效信息个数占比较小,空间密度小,占用大量空间。因此,有必要压缩存储稀疏矩阵。
稀疏矩阵的压缩方式是采用三元组的方法。每个三元组的三个值分别记录元素值、元素所在稀疏矩阵的行号和列号。
本节采用的压缩方式是使用一个规模更小的矩阵(三元组线性表)存储压缩后的稀疏矩阵。
- 记录数组一共有几行几列、有多少个不同值;
- 把具有不同值的元素的行列及其值记录在一个规模较小的数组中,从而缩小程序的规模;
稀疏矩阵的一种使用场景为五子棋游戏中双方棋子的位置,使用这种方法可以有效地压缩存储大小。下图展示了一个稀疏矩阵和其对应的三元组线性表的例子:
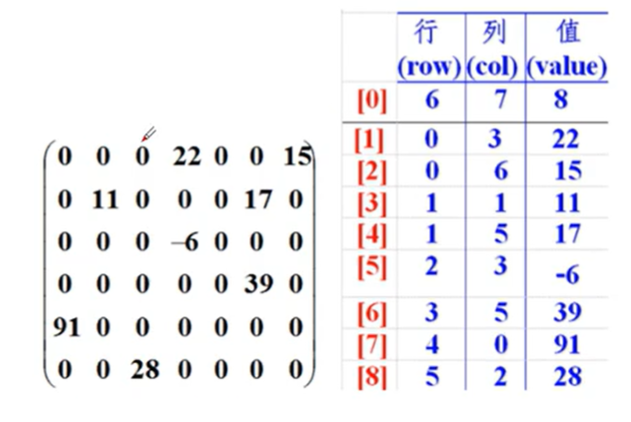
2-2.3 使用三元组线性表压缩稀疏矩阵
在转换之前,首先得明确稀疏矩阵应该存储什么内容。
稀疏矩阵是一个二维数组,由 4-6.1 中的图可知,它的首行存储原数组的行数列数和有效值个数,剩余行数用于存储有效值所在行、所在列和其对应值。
我们以下面的一个简单五子棋棋盘的数组开始:
// 原始棋盘矩阵是一个稀疏矩阵
int[][] checkerboard = new int[11][11];
checkerboard[2][1] = 1; // 以 1 为黑子
checkerboard[3][2] = 2; // 以 2 为白子
接下来,我们将这个稀疏矩阵逐步压缩至线性表中。首先,先找出稀疏矩阵中有效值的个数;
// 记录稀疏矩阵中有效值的个数
int num = 0;
// 遍历原矩阵,记录有效值个数
for (int i = 0; i < checkerboard.length; i++) {
for (int j = 0; j < checkerboard[i].length; j++) {
if (checkerboard[i][j] != 0){
num++;
}
}
}
然后,创建线性表,先记录稀疏矩阵的规模和有效值个数:
// 创建三元组线性表,采用规模更小的矩阵实现
// 头部信息:原数组的基本信息 - 行、列、有效值个数
int[][] sequentialList = new int[num+1][3]; // 线性表有额外的一行存储稀疏矩阵的规模和有效值个数
sequentialList[0][0] = checkerboard.length;
sequentialList[0][1] = checkerboard[0].length;
sequentialList[0][2] = num;
最后,向线性表中写入稀疏矩阵的有效值:
// 存储有效值
// 存储信息:有效值的所在行、列、有效值
int count = 0; // 当前正在写入的三元组线性表的所在行索引
for (int i = 0; i < checkerboard.length; i++) {
for (int j = 0; j < checkerboard[i].length; j++) {
if (checkerboard[i][j] != 0) {
count++; // 也可初始化为 1,在每次写完一行后自增
sequentialList[count][0] = i;
sequentialList[count][1] = j;
sequentialList[count][2] = checkerboard[i][j];
}
}
}
至此,稀疏矩阵压缩完成。
2-2.4 通过三元组线性表还原稀疏矩阵
以上述的五子棋棋盘为例,我们还希望根据压缩后的信息还原原矩阵的信息。根据三元组提供的信息即可还原。
// 还原稀疏矩阵
int[][] sparseMatrix = new int[sequentialList[0][0]][sequentialList[0][1]]; // 从线性表中读取原矩阵规模
for (int i = 1; i < sequentialList.length; i++) { // 注意 i = 1 开始
sparseMatrix[ sequentialList[i][0] ][ sequentialList[i][1] ] = sequentialList[i][2];
}
最后,我们将三个数组都打印出来,对比一下三者之间的相同点和差异,体会稀疏矩阵在压缩数据上的特点。

2-2.5 对称矩阵压缩存储
若一个 \(n\) 阶方阵 \(A[n][n]\) 中的元素满足 \(a_{i,j} = a_{j,i}, (0 \leq i, j \leq n-1)\),则称该方阵为 \(n\) 阶对称矩阵(symmetric matrix)。
显然,对于一个 \(n\) 阶对称矩阵而言,其主对角线以下部分(或以上部分)与另一部分信息完全相同,因此可以只存储其中一部分的信息从而压缩存储对称矩阵,即使用一维数组压缩存储对称矩阵。
对称矩阵可分为三个部分:主对角线、上三角和下三角部分。
存储对角线及下三角部分:若存储下三角部分,则原矩阵索引和压缩数组索引的对应关系为:
第 0 行 第 1 行 第 i 行,第 j 个 第 n-1 行
共 1 个 共 2 个 以等差数列形式递增 等差数列求和
a[0,0] a[0,1] a[1,1] ··· a[i,0] a[i,1] ··· a[i,j-1] a[i,j] ··· a a[i,i] ··· a[n-1,0] ··· a[n-1,n-1]
0 1 ······ k ······
则对于一个 \(n\) 阶对称矩阵而言,按下三角方式存储,压缩数组长度为 \(\frac{n(n+1)}{2}\)。对于原矩阵中第 \(i\) 行第 \(i\) 个元素(存储索引),其索引为:
存储上三角部分:存储上三角元素时,有 \(i < j\),其值等于 \(a_{j,i}\),即上述存储对角线和下三角部分的情况,则有:
2-2.6 三角矩阵压缩存储
矩阵的下三角部分的元素均为常数 \(c\) 的 \(n\) 阶方阵称为 \(n\) 阶上三角矩阵(upper triangular matrix)。反之,上三角部分的元素均为常数 \(c\) 的 \(n\) 阶方阵称为 \(n\) 阶下三角矩阵(lower triangular matrix)。
上三角矩阵:对于上三角矩阵中的元素 \(a_{i,j}, (i \leq j)\),其对应压缩数组中的索引 \(k\) 的关系有(全为存储索引)
-
对于存储在主对角线或上三角部分的元素,其前面共存储了 \(i\) 行元素(第 \(0\) 行存储了 \(n\) 个元素,第 \(1\) 行存储了 \(n-1\) 个元素,第 \(i-1\) 行存储了 \(n - i + 1\) 个元素),而在第 \(i\) 行中,\(a_{i,j}\) 前面又有 \(j - i\) 个元素。综上,有
\[k = \frac{i(2n - i + 1)}{2} + j - i, (i \leq j) \] -
对于存储在下三角部分的元素,其值为常数 \(c\),存储在数组的最后一个位置即可,即其索引为
\[k = \frac{n(n+1)}{2}, (i > j) \]
下三角矩阵:采用和上三角矩阵同样的压缩方法,推导过程类似,对于下三角矩阵中的元素 \(a_{i,j}, (i \geq j)\),其对应压缩数组中的索引 \(k\) 的关系有(全为存储索引)
-
对于存储在主对角线或下三角部分的元素,其前面共存储了 \(i\) 行元素(第 \(0\) 行存储了 \(1\) 个元素,第 \(1\) 行存储了 \(2\) 个元素,按等差数列正向递增,第 \(i-1\) 行存储了 \(i\) 个元素),而在第 \(i\) 行中,\(a_{i,j}\) 前面又有 \(j\) 个元素。综上,有
\[k = \frac{i(i + 1)}{2} + j, (i \geq j) \] -
对于存储在上三角部分的元素,其值为常数 \(c\),存储在数组的最后一个位置即可,其索引为
\[k = \frac{n(n+1)}{2}, (i < j) \]
2-2.7 对角矩阵压缩存储
若一个 \(n\) 阶方阵 \(A\) 满足其所有非零元素都集中在以主对角线为中心的带状区域中,则称该方阵为 \(n\) 阶对角矩阵(diagonal matrix)。
如图所示,对角矩阵主对角线的上、下方各有 \(b\) 条非零元素构成的次对角线,称 \(b\) 为半带宽,则矩阵带宽为 \(2b + 1\)(含主对角线)。
以一个 \(b = 1\) 的三对角矩阵为例,只将其非零元素 \(a_{i,j}\) 压缩存储到一个一维数组中,对应数组元素 \(b_k\)。
-
矩阵中行索引为 \(0\) 和行索引为 \(n-1\) 的行中都只有两个非零元素,其余各行都有 3 个非零元素;
-
对于行索引不为零的非零元素 \(a_{i,j}\),其前面存储了矩阵的前 \(i\) 行元素,即有 \(2 + 3(i - 1)\) 个元素,元素 \(a_{i,j}\) 在该行有三种情况:
- 若 \(a_{i,j}\) 为该行首个元素,则 \(j = i - 1\),其压缩数组索引为 \(k = 2 + 3(i - 1) = 3i - 1\);
- 若 \(a_{i,j}\) 为该行第二个元素,则 \(j = i\),其压缩数组索引为 \(k = 2 + 3(i - 1) + 1 = 3i\);
- 若 \(a_{i,j}\) 为该行第三个元素,则 \(j = i + 1\),其压缩数组索引为 \(k = 2 + 3(i - 1) + 2 = 3i + 1\);
综上,即可得到 \(k = 2i + j\)。
对于不同规模、不同带宽的对角矩阵,其压缩方法都是通过发现规律,从而将有规律分布的数据压缩存储到同一片存储空间中。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号