洛谷 P2921 在农场万圣节Trick or Treat on the Farm题解

题意翻译

题目描述

每年，在威斯康星州，奶牛们都会穿上衣服，收集农夫约翰在N(1<=N<=100，000)个牛棚隔间中留下的糖果，以此来庆祝美国秋天的万圣节。

由于牛棚不太大，FJ通过指定奶牛必须遵循的穿越路线来确保奶牛的乐趣。为了实现这个让奶牛在牛棚里来回穿梭的方案，FJ在第i号隔间上张贴了一个“下一个隔间”Next_i(1<=Next_i<=N)，告诉奶牛要去的下一个隔间；这样，为了收集它们的糖果，奶牛就会在牛棚里来回穿梭了。

FJ命令奶牛i应该从i号隔间开始收集糖果。如果一只奶牛回到某一个她已经去过的隔间，她就会停止收集糖果。

在被迫停止收集糖果之前，计算一下每头奶牛要前往的隔间数（包含起点）。

输入格式

第1行 整数n。

第2行到n+1行 每行包含一个整数 next_i 。

输出格式

n行，第i行包含一个整数，表示第i只奶牛要前往的隔间数。

样例解释

有4个隔间

隔间1要求牛到隔间1

隔间2要求牛到隔间3

隔间3要求牛到隔间2

隔间4要求牛到隔间3

牛1，从1号隔间出发，总共访问1个隔间；

牛2，从2号隔间出发，然后到三号隔间，然后到2号隔间，终止，总共访问2个隔间；

牛3，从3号隔间出发，然后到2号隔间，然后到3号隔间，终止，总共访问2个隔间；

牛4，从4号隔间出发，然后到3号隔间，然后到2号隔间，然后到3号隔间，终止，总共访问3个隔间。

翻译提供者：吃葡萄吐糖

题目描述

Every year in Wisconsin the cows celebrate the USA autumn holiday of Halloween by dressing up in costumes and collecting candy that Farmer John leaves in the N (1 <= N <= 100,000) stalls conveniently numbered 1..N.

Because the barn is not so large, FJ makes sure the cows extend their fun by specifying a traversal route the cows must follow. To implement this scheme for traveling back and forth through the barn, FJ has posted a 'next stall number' next_i (1 <= next_i <= N) on stall i that tells the cows which stall to visit next; the cows thus might travel the length of the barn many times in order to collect their candy.

FJ mandates that cow i should start collecting candy at stall i. A cow stops her candy collection if she arrives back at any stall she has already visited.

Calculate the number of unique stalls each cow visits before being forced to stop her candy collection.

POINTS: 100

输入格式

* Line 1: A single integer: N

* Lines 2..N+1: Line i+1 contains a single integer: next_i

输出格式

* Lines 1..N: Line i contains a single integer that is the total number of unique stalls visited by cow i before she returns to a stall she has previously visited.

输入输出样例

输入 #1复制

4 
1 
3 
2 
3 

输出 #1复制

1 
2 
2 
3 

说明/提示

Four stalls.

* Stall 1 directs the cow back to stall 1.

* Stall 2 directs the cow to stall 3

* Stall 3 directs the cow to stall 2

* Stall 4 directs the cow to stall 3

Cow 1: Start at 1, next is 1. Total stalls visited: 1.

Cow 2: Start at 2, next is 3, next is 2. Total stalls visited: 2. Cow 3: Start at 3, next is 2, next is 3. Total stalls visited: 2. Cow 4: Start at 4, next is 3, next is 2, next is 3. Total stalls visited: 3.

---

 

题解

这个题虽然是图的题目，但是它的图很特殊，每个节点的出度都是1，而且一定存在环。

直接暴力可以得40分。

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>

using namespace std;

const int MAXN = 1e5 + 5; 
int n, next[MAXN], vis[MAXN], ans[MAXN], p; 

int main()
{
 cin >> n;
 for(int i = 1; i <= n; i++)
 {
  cin >> next[i];
 }
 for(int i = 1; i <= n; i++)
 {
  memset(vis, 0, sizeof(vis));
  ans[i] = 1;
  p = i;
  vis[p] = 1;
  while(vis[next[p]] == 0)
  {
   vis[next[p]] = 1;
   p = next[p];
   ans[i]++;
  }
 }
 for(int i = 1; i <= n; i++)
 {
  cout << ans[i] << endl;
 }
 
 return 0;
}

剩下的问题就是如何解决TLE的问题。和01迷宫问题的思路类似，需要对图进行染色，找到环，同一个环上的各个节点的隔间数是相同的，把这个结果保存下来就可以减少后续的运算量了。下图是样例染色的结果。1号节点是个自环长度为1,2和3号节点是长度为2的环，所以这两个节点输出的隔间数都是环的长度2。4号节点经过1步走到2和3组成的环，所以它的隔间数是1+2=3。

 染色的过程有两种可能：

1）染色的过程遇到了同种颜色的节点，例如下图中2-3-4-3。

2）染色的过程中遇到了不同颜色的节点，例如下图中的5-2和6-4。

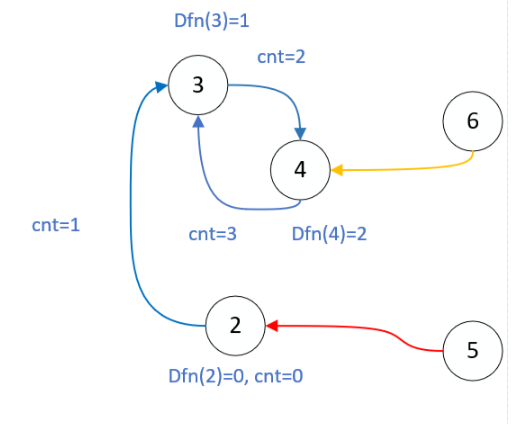
为了方便计算环的长度和走过的隔间数，我们引入两个变量：cnt和dfn数组。cnt从0开始，用于计算此次染色所经过的隔间数，每走一次加1。dfn记录每个节点和此次染色第一个节点之间的距离。例如第一种染色情况，dfn(2)=0，dfn(3)=1,dfn(4)=2。当从4走到3时，我们立刻可以发现一个同色节点组成的环。环的长度是cnt-dfn(3)=2。而且我们可以记录下这个颜色路径进入环的第一个节点是3号节点。

对于第2种染色过程，又分为两种情况：

1）所遇到的不同颜色的节点在环上，如4号节点。这种情况隔间数等于cnt+环长。

2）所遇到的不同颜色的节点不在环上，如2号节点。这种情况隔间数等于cnt+环长+从所遇到的节点到第一个进入环的节点的距离。

而判断节点是否在环上，可以用dfn的大小进行比较，所有比第一个进入环的节点的dfn小的节点都在环外，反之在环上。

下面就是改进后的代码：

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>

using namespace std;

const int MAXN = 1e5 + 5; 
int n, next[MAXN], vis[MAXN], ans[MAXN], p; 
int dfn[MAXN], cnt;
int looplen[MAXN]; // 环长 
int stloop[MAXN]; // 路径中进入环的第一个节点的dfn值 

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> next[i];
    }

    memset(vis, 0, sizeof(vis));
    for(int i = 1; i <= n; i++)
    {
        cnt = 0;
        p = i;
        while(vis[p] == 0)
        {
            vis[p] = i;
            dfn[p] = cnt;
            p = next[p];
            cnt++;
        }
        if(vis[p] == i)
        { // 走到了自己染色的环 
            ans[i] = cnt;
            looplen[i] = cnt - dfn[p];
            stloop[i] = dfn[p];
         } 
         else
         { // 走到了其他点染色的路径
             looplen[i] = looplen[vis[p]];
             stloop[i] = cnt;
             if(stloop[vis[p]] > dfn[p])
            { // 遇到的点不在环上 
                 stloop[i] += stloop[vis[p]] - dfn[p];
            }          
             ans[i] = stloop[i] + looplen[i];
         }
    }
    for(int i = 1; i <= n; i++)
    {
        cout << ans[i] << endl;
    }
    
    return 0;
}