20182303 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结

20182303 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结

目录

教材学习内容总结（Chapter19 图）

图的定义和基本术语

  • 定义：图是由顶点集合(Vertex)及顶点间的关系集合组成的一种数据结构:Graph＝( V, E )
    V={x|x∈某个数据对象 }是顶点的有穷非空集合；
    E={(x, y)|x,y∈V}是顶点之间关系的有穷集合，也也叫做边(Edge)集合。
  • 在图中的数据元素通常称为顶点V。
  • 无向边：若顶点x和y之间的边没有方向，则称该边为无向边(x,y)，(x,y)与(y,x)意义相同，表示x和y之间有连接。
  • 无向图：若图中任意两个顶点之间的边均是无向边，则称该图为无向图。
  • 有向边：若顶点x和y之间的边有方向，则称该边为有向边<x,y>，<x,y>与<y,x>意义不同，表示从x连接到y，x称为尾，y称为头。
  • 有向图：若图中任意两个顶点之间的边均是有向边，则称该图为有向图。
  • 邻接：是两个顶点之间的一种关系。如果图包含（u,v），则称顶点v与顶点u邻接。在无向图中，这也暗示了顶点u也与顶点v邻接。在无向图中邻接关系是对称的。
  • 关联：是指顶点和边之间的关系。在有向图中，边（u,v）从顶点u开始关联到v，或者相反，从顶点v开始关联到u。在无向图中，边(u,v)与顶点u和v相关联。
  • 完全图：每个顶点都与其他顶点相邻接的图。
  • 度(Degree)：顶点v的度是和v相关联的边的数目，记为TD(v)。
    • 入度：以v为头的边的数目，记为ID(v)
    • 出度：以v为尾的边的数目，记为OD(v)
    • TD(v)
      = ID(v) + OD(v)E
      = [TD(v1) + TD(v2) + … + TD(vn)] / 2E
      = ID(v1) + ID(v2) + … + ID(vn)E
      = OD(v1) + OD(v2) + … + OD(vn)
  • 权(Weight)：与图的边相关的数字叫做权，权常用来表示图中顶点间的距离或者耗费。
  • 带权的图通常称为网。
  • 路径：依次遍历顶点序列之间的边所形成的轨迹。没有重复顶点的路径称为简单路径。路径的长度是路径上的边或弧的数目。
  • 环：指路径包含相同的顶点两次或两次以上。也就是说，在有向图的一条路径中，如果从某顶点出发，最后能够返回该顶点，则该路径是环。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路称为简单环或简单回路。
  • 连通性是图中另一个重要的概念。
    • 对于无向图而言，如果它的每个顶点都能通过某条路径到达其他顶点，那么我们称它为联通的。
    • 如果该条件在有向图中同样成立，则称该图是强连通。
    • 尽管无向图可能不是连通的，但它可能包含连通的部分，这部分分支为连通分支。
    • 如果有向图中只有部分是强连通的，则该部分称为强连通分支。
    • 某些特定的顶点对于保护图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使得图或某分支失去连通性，则称该顶点为关结点

图的操作

  • 创建图结构
  • 遍历图
  • 对顶点的操作：查找、取值、赋值、插入、删除等
  • 对边的操作：插入、删除、存取或修改权值等

图的存储结构及实现

邻接矩阵

用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中的边或弧的信息。
例：

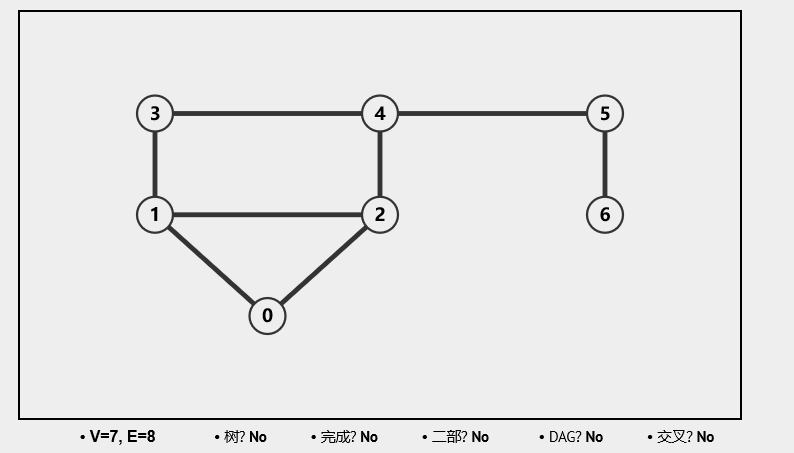
  • 时间复杂度：
    • 边查找：O(1)
    • 顶点度查找：O(n)
  • 空间复杂度：O(n^2)

边集数组

利用一维数组存储图中所有边的一种图的表示方法
上例：

  • 时间复杂度：若该图有e条边，n个顶点，则查找一条边或一个顶点的度的时间复杂度都为O(e)。
  • 空间复杂度：O(n+e)

邻接表

（1）图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过，数组可以较容易的读取顶点的信息，更加方便。
（2）图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。

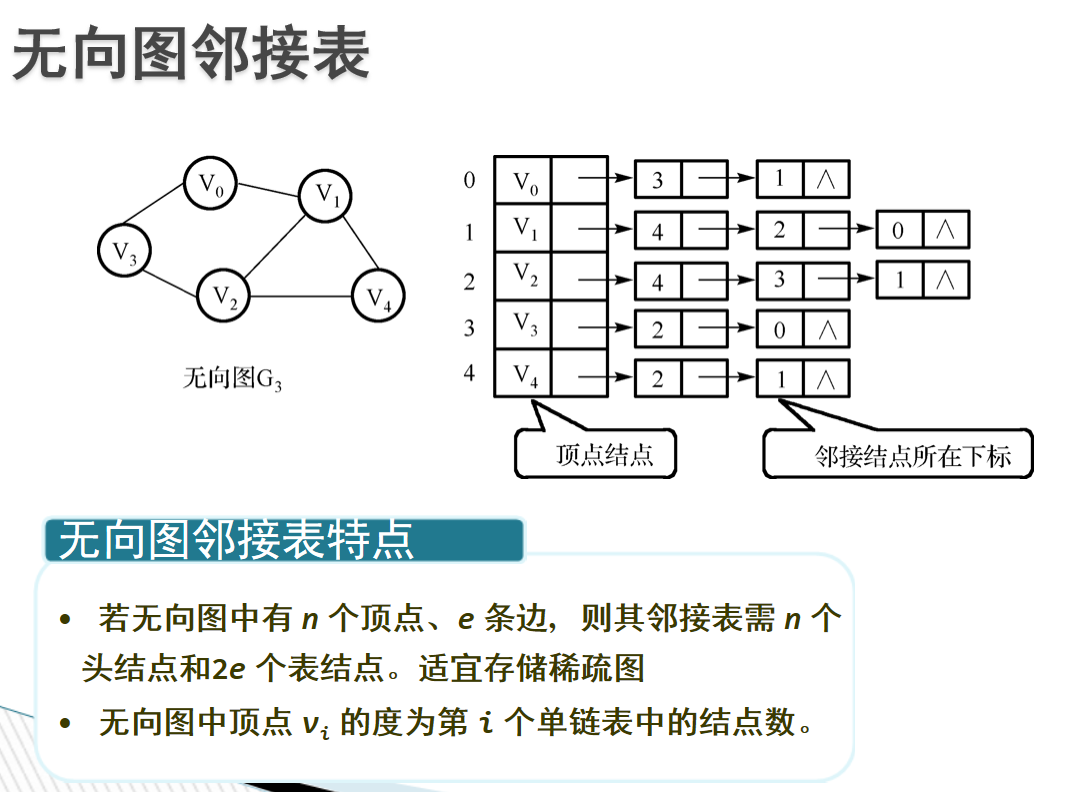
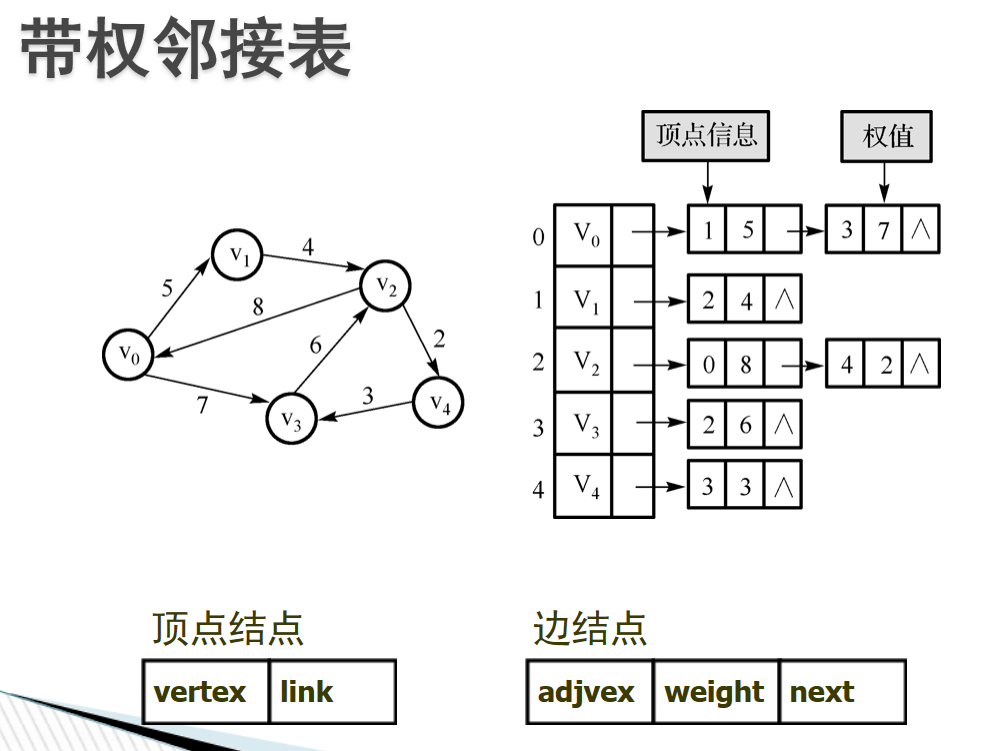
上例：

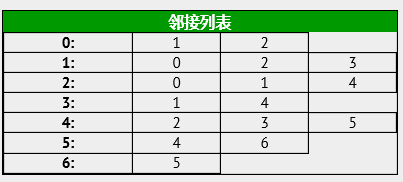
  • 空间复杂度：O(n+e)

十字链表

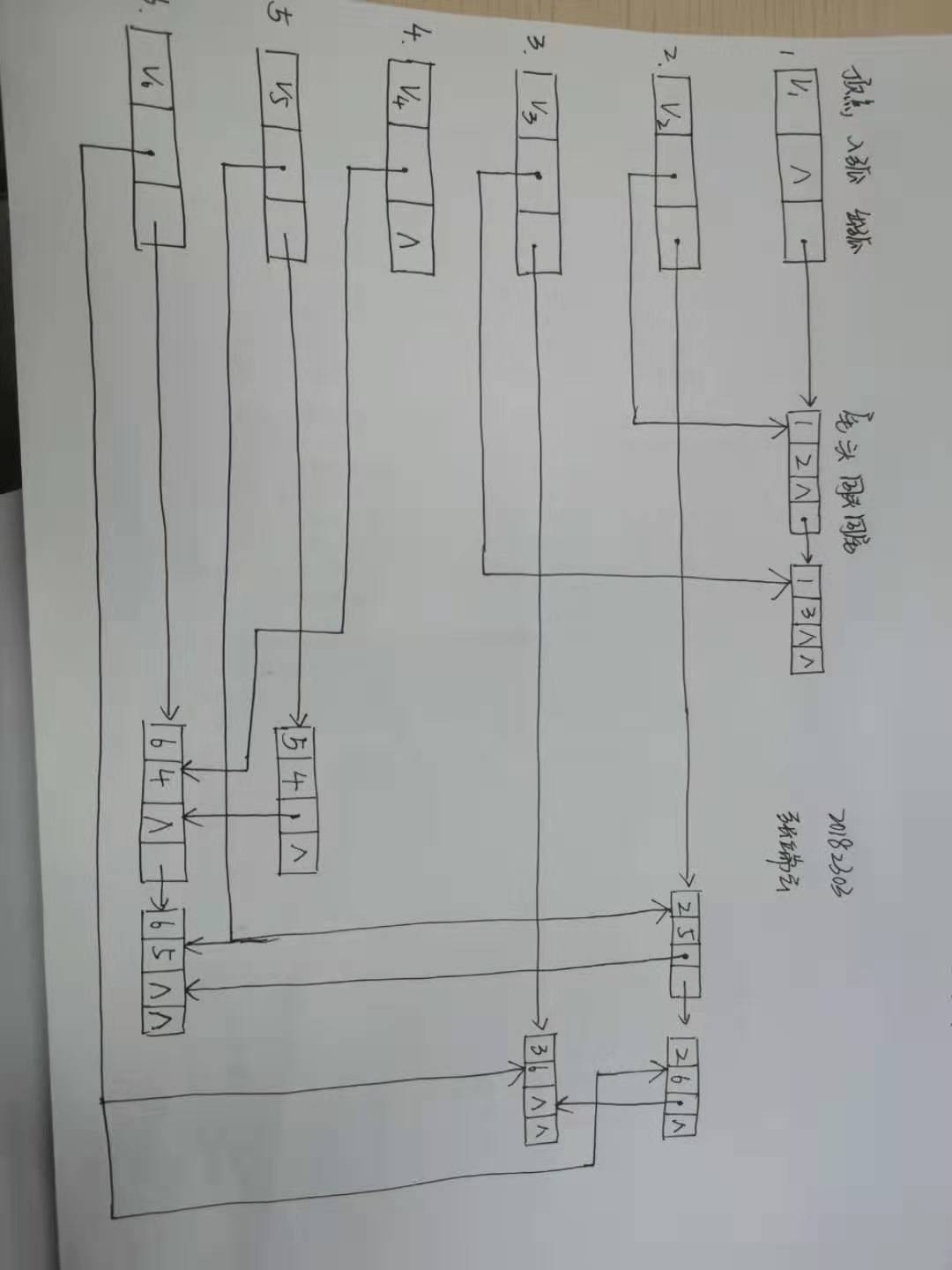
图存储结构归纳比较

表 1　几种图的存储结构的比较

Tab1　The Comparsion of Several Graph for Storing Structures

名称 实现方法 优点 缺点 时间复杂度
邻接矩阵 二维数组 易判断两点间的关系,容易求得顶点的度 占用空间大 O(n2+m*n)2
邻接表 链表 节省空间,易得到顶点的出度 不易判断两点间的关系,不易得到顶点的入度 O(n+m)或O(n*m)
十字链表 链表 空间要求较小,易求得顶点的出度和入度 结构较复杂 同邻接表
邻接多重表 链表 节省空间,易判断两点间的关系 结构较复杂 同邻接表

图的遍历

以v为起始点，由近至远，依次访问和v有路径相通且路径长度为1,2,...的顶点的过程。

从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。

教材学习中的问题和解决过程

  • 问题1：深度优先遍历无序列表栈的变化过程？

  • 问题1解决方案：

    • 算法表述
      1.访问初始结点v，并标记结点v为已访问。
      2.查找结点v的第一个邻接结点w。
      3.若w存在，则继续执行4，否则算法结束。
      4.若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
      5.查找结点v的w邻接结点的下一个邻接结点，转到步骤3。
    • 过程分析：

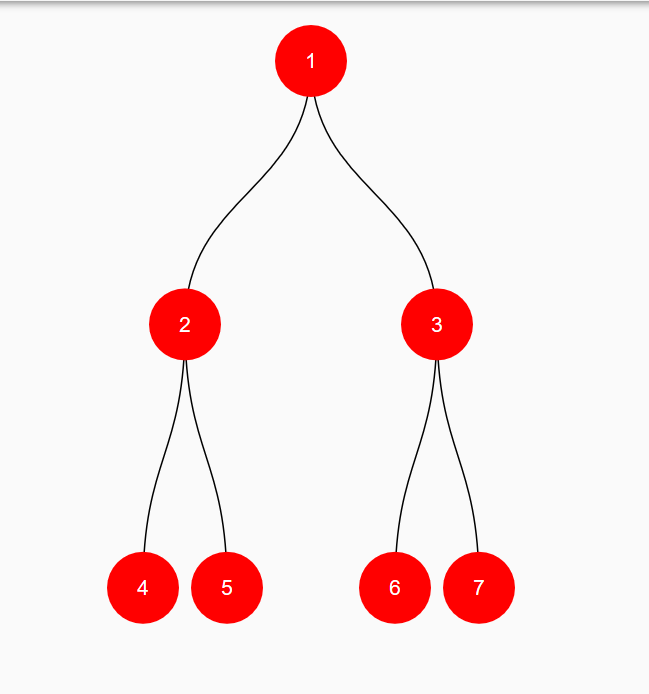
    （1）首先节点 1 进栈，节点1在栈顶；
    （2）然后节点1出栈，访问节点1，节点1的孩子节点3进栈，节点2进栈；
    （3）节点2在栈顶，然后节点2出栈，访问节点2
    （4）节点2的孩子节点5进栈，节点4进栈
    （5）节点4在栈顶，节点4出栈，访问节点4，
    （6）节点4左右孩子为空，然后节点5在栈顶，节点5出栈，访问节点5；
    （7）节点5左右孩子为空，然后节点3在站顶，节点3出栈，访问节点3；
    （8）节点3的孩子节点7进栈，节点6进栈
    （9）节点6在栈顶，节点6出栈，访问节点6；
    （10）节点6的孩子为空，这个时候节点7在栈顶，节点7出栈，访问节点7
    （11）节点7的左右孩子为空，此时栈为空，遍历结束。

代码调试中的问题和解决过程

  • 问题1：广度优先遍历测试时空指针异常。
  • 问题1解决方案：将enqueue方法修改为↓
public void enqueue(T element)
    {
        LinearNode<T> node = new LinearNode<T>(element);

        if (isEmpty())
            head = node;
        else
            tail.setNext(node);

        tail = node;
        count++;
    }

代码托管

Chapter19

上周考试错题总结

  1. To maintain the completeness of the tree, there is only one valid element to replace the root, and that is the element stored in the first leaf in the tree.
    A .True
    B .False
    正确答案： B 你的答案： A
    解析：为了保持树的完整性，只有一个有效的元素可以替换这个元素，那就是存储在树的最后一个叶子中的元素。

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 10000行 30篇 400小时
第一周 254/254 2/2 21/21 开始编写简单的程序
第二周 132/386 1/3 26/47 学会使用Scanner类
第三周 632/1018 2/5 21/68 学会使用部分常用类
第四周 663/1681 2/7 27/95 junit测试和编写类
第五周 1407/3088 2/9 30/125 继承以及继承相关类与关键词
第六周 2390/5478 1/10 25/150 面向对象三大属性&异常
第七周 1061/6539 2/12 25/175 算法，栈，队列，链表
第八周 813/7352 2/14 26/201 查找与排序
第九周 3424/10776 3/17 25/226 树&二叉查找树
第九周 1770/12546 2/19 30/256 图&深入了解安卓布局

  • 计划学习时间:25小时

  • 实际学习时间:30小时

参考资料

posted @ 2019-11-25 22:24  zdyyy  阅读(154)  评论(0)  编辑  收藏  举报