20182303 2019-2020-1 《数据结构与面向对象程序设计》实验7报告
课程:《程序设计与数据结构》
班级: 1823
姓名:张端云
学号:20182303
实验教师:王志强
实验日期:2019年10月30日
必修/选修: 必修
实验内容
- 定义一个Searching和Sorting类,并在类中实现linearSearch,SelectionSort方法,最后完成测试。
要求:不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位。
提交运行结果图。 - 重构你的代码
- 把Sorting.java Searching.java放入 cn.edu.besti.cs1823.(姓名首字母+四位学号) 包中;
- 把测试代码放test包中,重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)。
- 参考 http://www.cnblogs.com/maybe2030/p/4715035.html ,学习各种查找算法并在Searching中补充查找算法并测试,提交运行结果截图。
- 补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个),测试实现的算法(正常,异常,边界),提交运行结果截图。
- 编写Android程序对实现各种查找与排序算法进行测试,提交运行结果截图,推送代码到码云(选做)。
实验过程及结果
point1
Searching
要求在类中实现linearSearch方法,并完成测试。
public static Comparable LinearSearch(Comparable[] data,Comparable target)
{
Comparable result=null;
int index=0;
while(result==null&&index<data.length)
{
if(data[index].compareTo(target)==0)
result=data[index];
index++;
}
return result;
}
测试:

Sorting
要求在类中实现SelectionSort方法,并完成测试
public static void selectionSort(Comparable[] data) {
int min;
for (int index = 0; index < data.length - 1; index++) {
min = index;
for (int scan = index + 1; scan < data.length; scan++)
if (data[scan].compareTo(data[min]) < 0)
min = scan;
swap(data, min, index);
}
}
测试:
-
正序、逆序、乱序测试
-
空指针异常测试
-
越界异常测试
point2
把Sorting.java、Searching.java放入 cn.edu.besti.cs1823.Zdy2303中,并完成测试。
IDEA测试
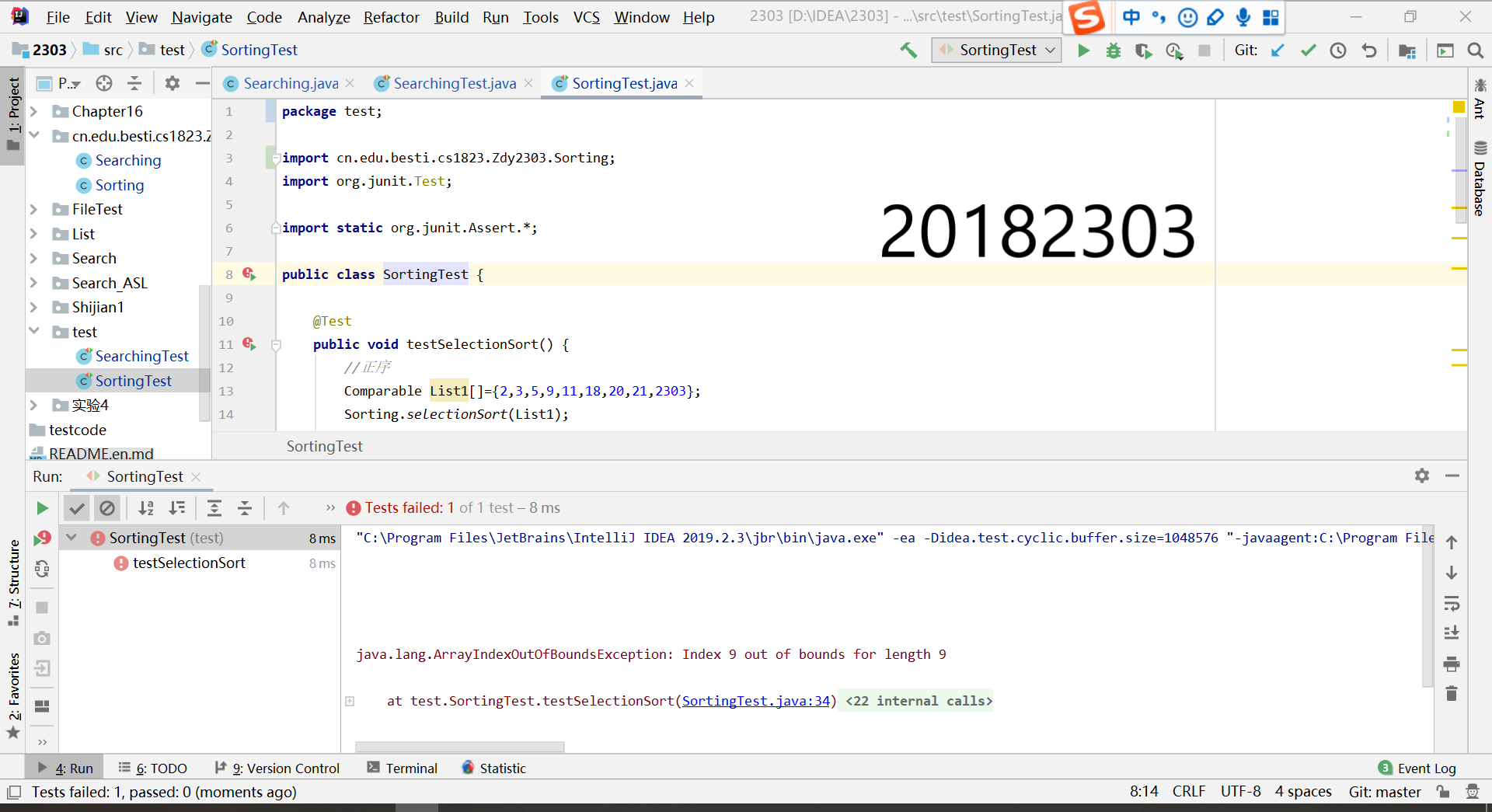
命令行测试
point3
学习各种查找算法并在Searching中补充查找算法并测试。
补充的查找算法有:二分查找、插入查找、斐波那契查找。
- 二分查找
public static Comparable binarySearch(Comparable[] data,Comparable target)
{
Comparable result=null;
int first=0,last=data.length,mid;
while(result==null&&first<=last)
{
mid=(first+last)/2;
if(data[mid].compareTo(target)==0)
result=data[mid];
else
if(data[mid].compareTo(target)>0)
last=mid-1;
else
first=mid+1;
}
return result;
}
- 插入查找
public static<T> boolean linearSearch(T[] data,int min,int max,T target)
{
int index=min;
boolean found=false;
while(!found&&index<=max)
{
found=data[index].equals(target);
index++;
}
return found;
}
- 斐波那契查找
- 斐波那契数列:又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34.....在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)
- 斐波那契查找:斐波那契查找同样是基于二分查找实现的,只不过它是根据斐波那契数列的特点对数组进行划分,将key值与temp[mid](mid = low+Fibonacci(k-1)-1)进行比较,分为三种情况:
当key=temp[mid]时,mid即为查找元素在数组中的索引值;
当key>temp[mid]时,在temp数组的左边继续进行查找;
当key<temp[mid]时,在temp数组的右边继续进行查找。
public static int Fibonacci(int n) {
if(n == 0) {
return 0;
}
if(n == 1) {
return 1;
}
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
public static int FibonacciSearch(int[] data,int n,int key) {
int low = 1;
int high = n;
int mid;
// 寻找k值,k值要求k值能使得F[k]-1恰好大于或等于n
int k = 0;
while (n > Fibonacci(k) - 1) {
k++;
}
//因为无法直接对原数组增加长度,所以定义一个新的数组
//采用System.arraycopy()进行数组间的赋值
int[] temp = new int[Fibonacci(k)];
System.arraycopy(data, 0, temp, 0, data.length);
//对数组中新增的位置进行赋值
for (int i = n + 1; i <= Fibonacci(k) - 1; i++) {
temp[i] = temp[n];
}
while (low <= high) {
mid = low + Fibonacci(k - 1) - 1;
// 在mid的左边进行查找
if (temp[mid] > key) {
high = mid - 1;
k = k - 1;
}
// 在mid的右边进行查找
else if (temp[mid] < key) {
low = mid + 1;
k = k - 2;
} else {
if (mid <= n) {
return mid;
}
//当mid位于新增的数组中时,返回n
else {
return n;
}
}
}
return 0;
}
测试:
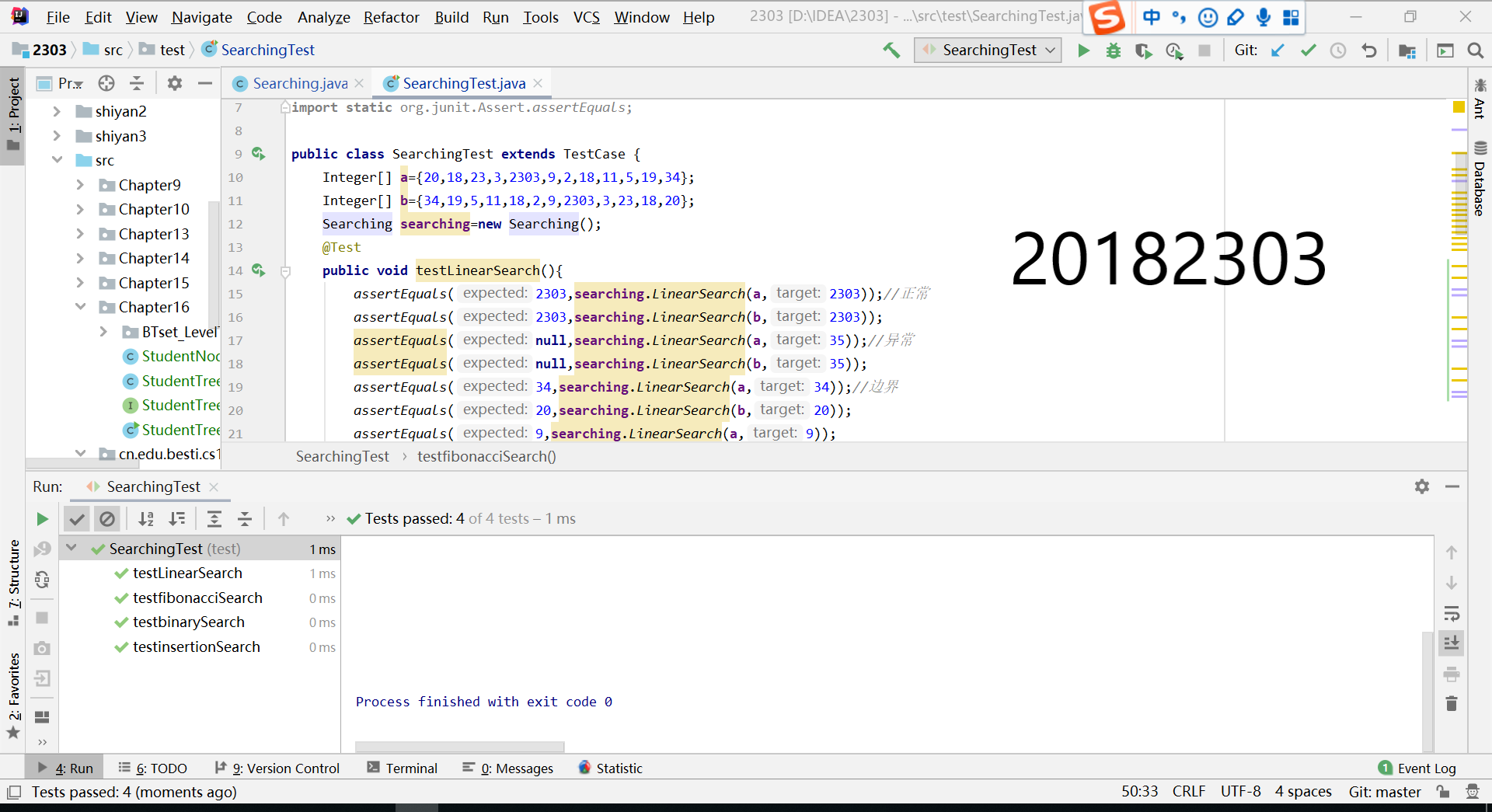
point4
补充实现排序方法:希尔排序,堆排序,二叉树排序等(至少3个),并完成测试(正常,异常,边界)。
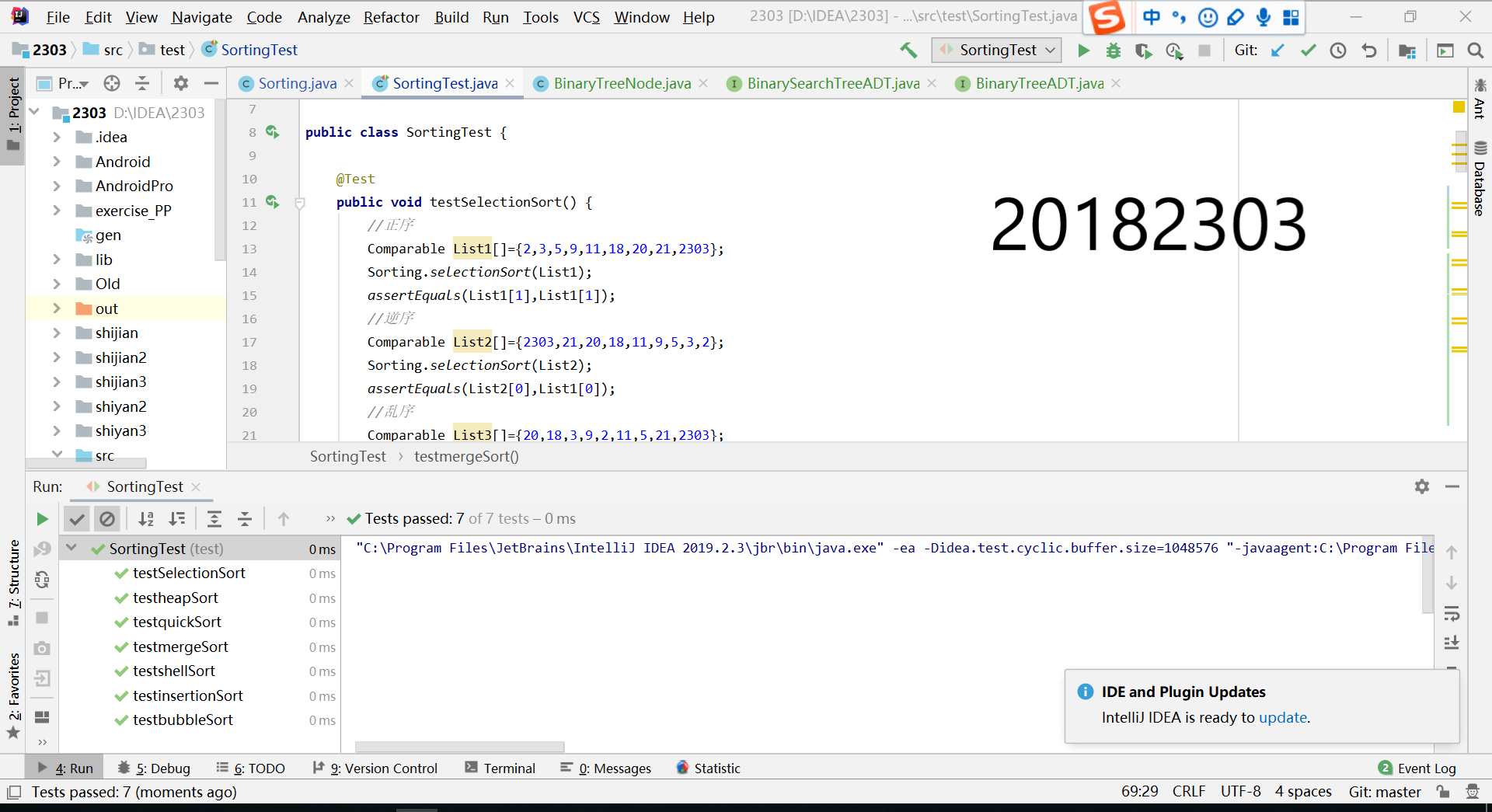
point5
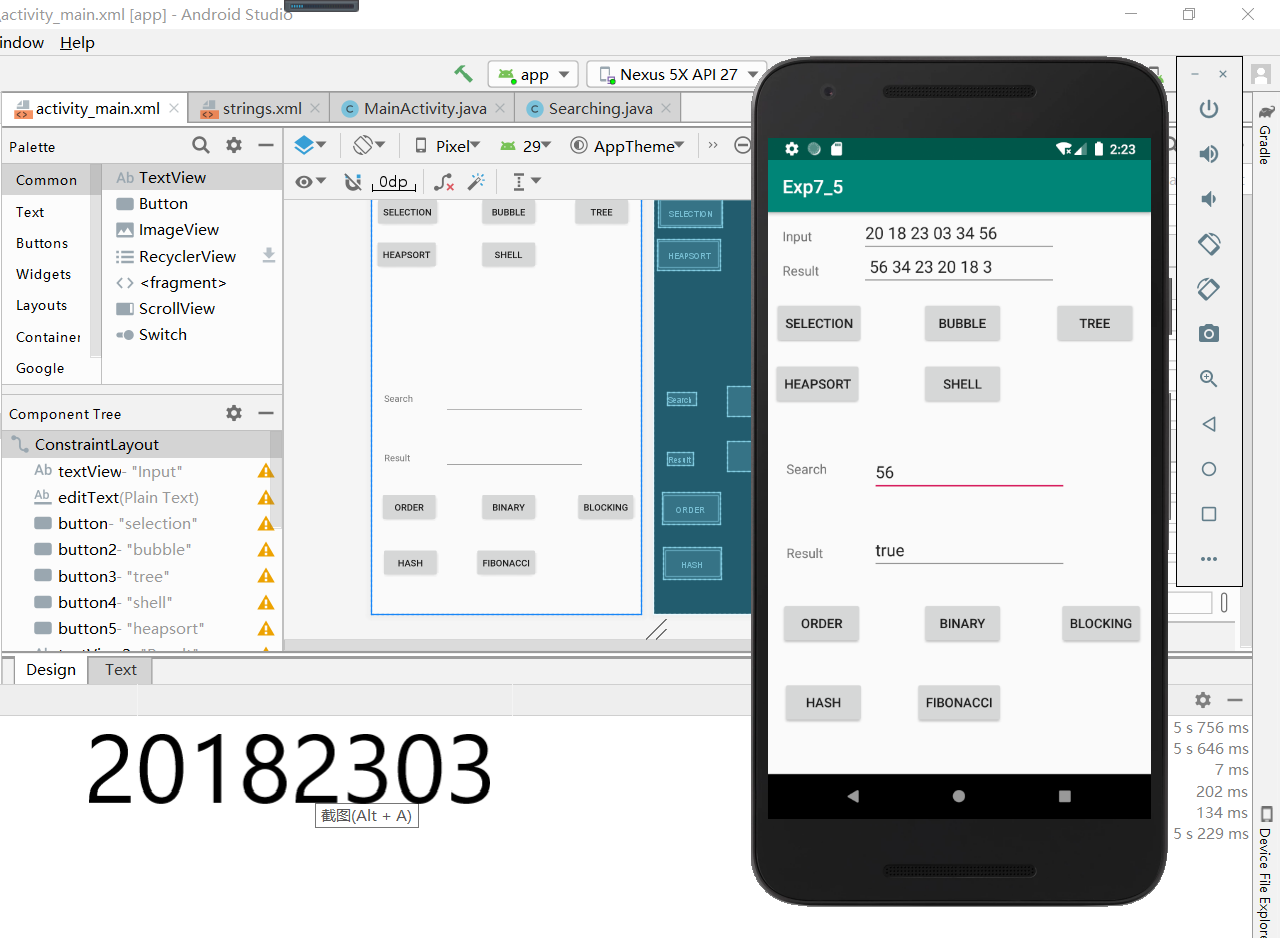
编写Android程序对实现各种查找与排序算法进行测试。
3. 实验过程中遇到的问题和解决过程
-
问题1:在完成命令行测试时,发现命令行中不能使用junit测试。
-
问题1解决方案:Ubuntu单元测试JUnit的使用
由以上链接,理论上命令行实现junit是可行的,然而我并没有尝试成功...只能编写驱动程序进行测试。
其他(感悟、思考等)
本次实验发现自己对于linux命令行的操作已经有些生疏,知识果然不会一直乖乖的待在自己脑子里,三天不复习,知识就会上房揭瓦。


