20182303 2019-2020-1 《数据结构与面向对象程序设计》第8周学习总结
目录
教材学习内容总结
Chapter13 查找与排序
- 查找
1.线性查找:从表头开始,依次将每个值与目标元素进行比较。
public static<T>
boolean linearSearch(T[] data,int min,int max,T target)
{
int index=min;
boolean found=false;
while(!found&&index<=max)
{
found=data[index].equals(target);
index++;
}
return found;
}
线性查找的平均时间复杂度为O(n)。
2.二分查找:在一个已排序的项目组中,从列表的中间开始查找,如果中间元素不是要找的指定元素,则削减一半查找池,从剩余一半的查找池(可行候选项)中继续以与之前相同的方式进行查找,多次循环直至找到目标元素或确定目标元素不在查找池中。
public static <T extends Comparable<T>>
boolean binarysearch (T[] data, int min, int max,int mid,T target)
{
boolean found = false;
//int mid = (min + max) / 2;
if(data[mid].compareTo(target)==0)
found = true;
else if (data[mid].compareTo(target)>0)
{
if(min<mid-1)
{
mid--;
found = binarysearch(data,min,max,mid,target);
}
}
else if(mid+1<=max)
{
mid++;
found = binarysearch(data,min,max,mid,target);
}
return found;
}
二分查找的平均时间复杂度为O(log2n)。
3.分块查找——索引顺序表:先折半查找,再线性查找,性能介于两者之间。

4.散列查找——除留余数法:用关键字k除以不大于散列表长度的数m所得余数作为哈希地址,即有:H(k)=k%m 。
- 排序
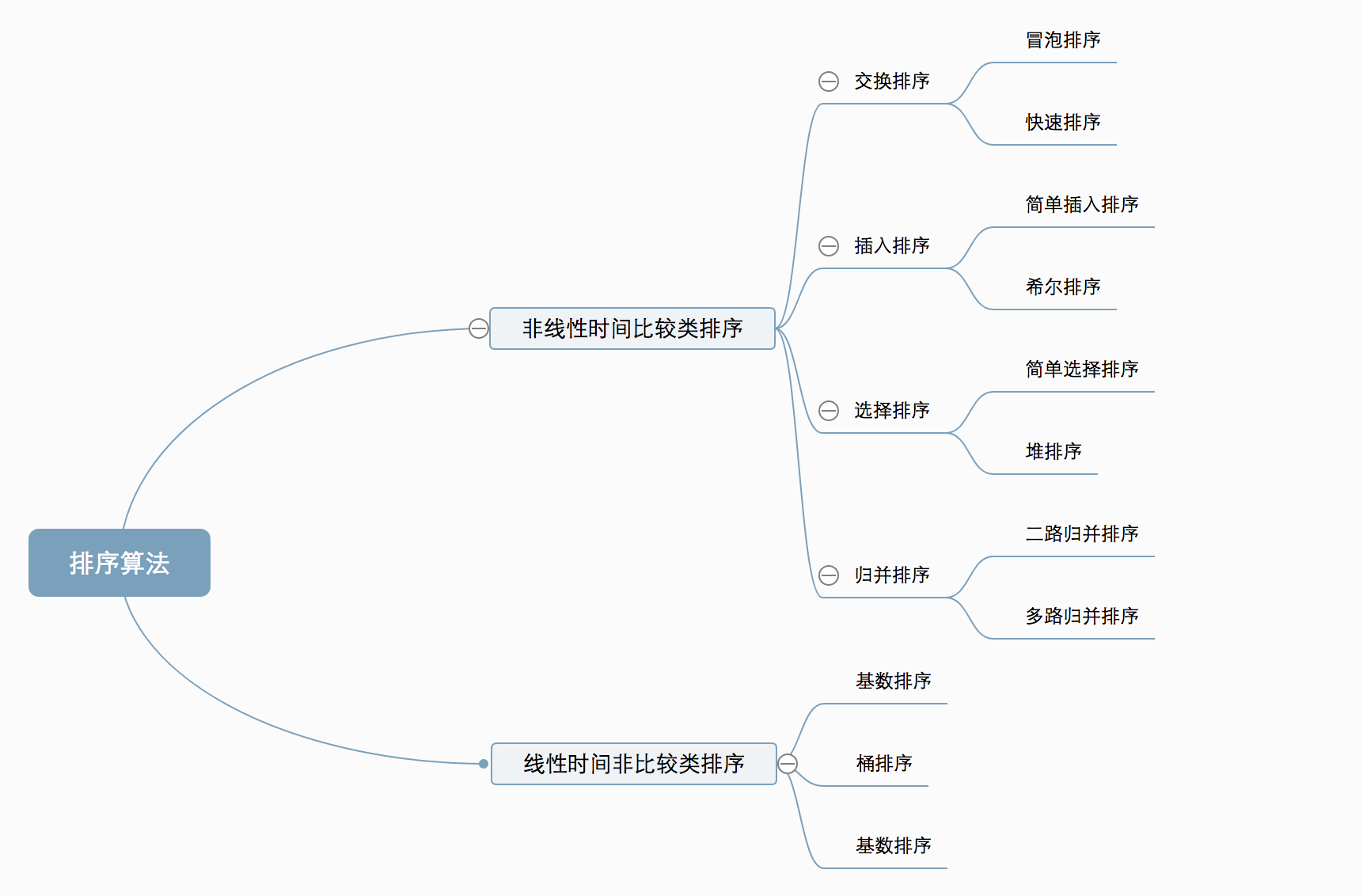
1.插入排序
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
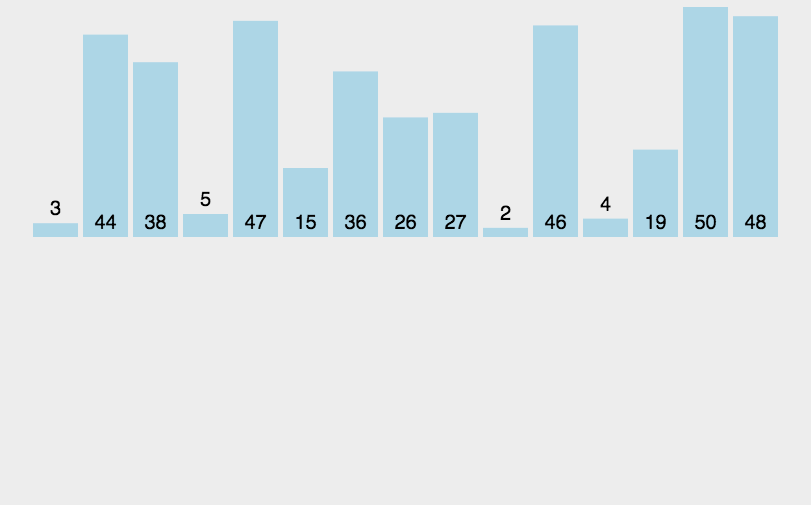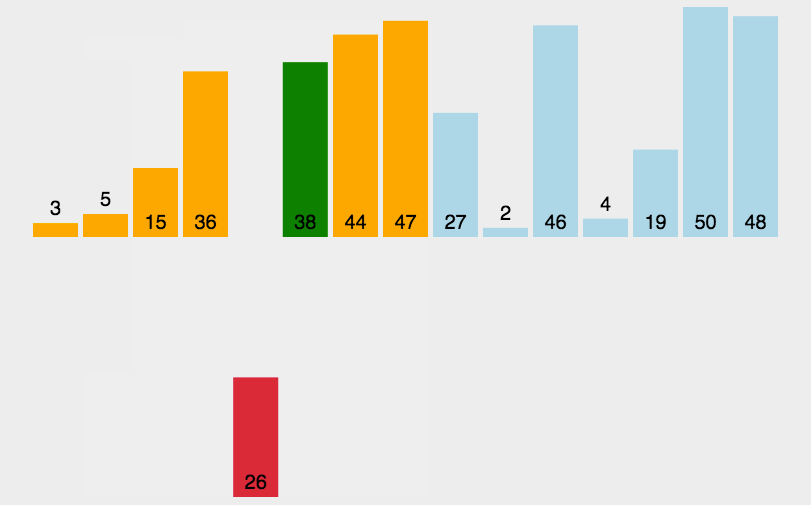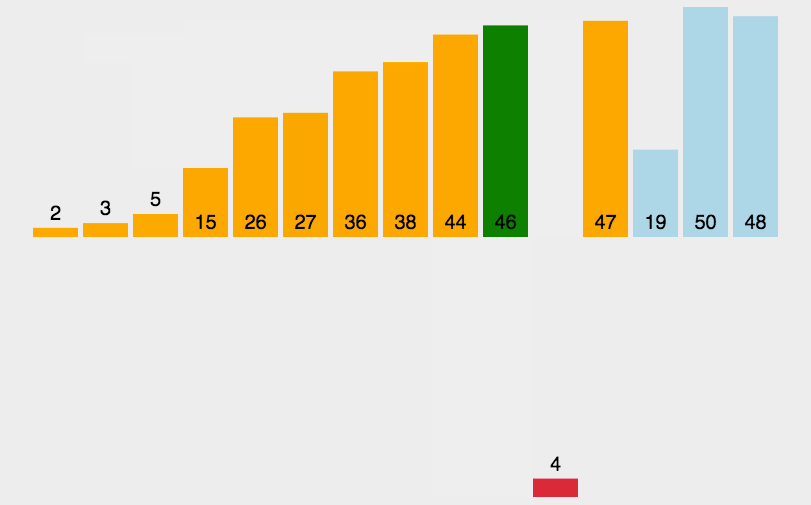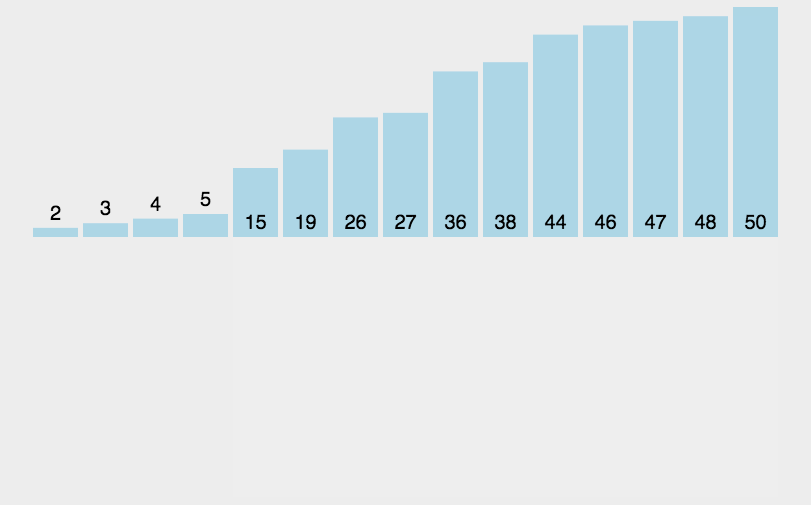
实现:
public static <T extends Comparable<T>> void insertionSort(T[] data)
{
//循环次数为n,时间复杂度为O(n)
for (int index = 1; index < data.length; index++)
{
T key = data[index];
int position = index;
//循环次数为n,时间复杂度为O(n)
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1];
position--;
}
data[position] = key;
}
}
2.交换排序
- 冒泡排序:通过反复比较相邻元素的大小并在必要时进行互换,最终实现排序。
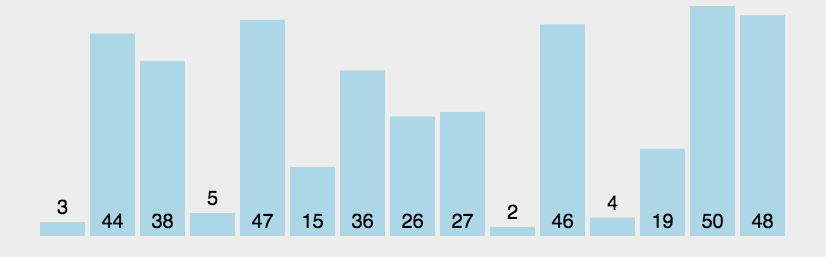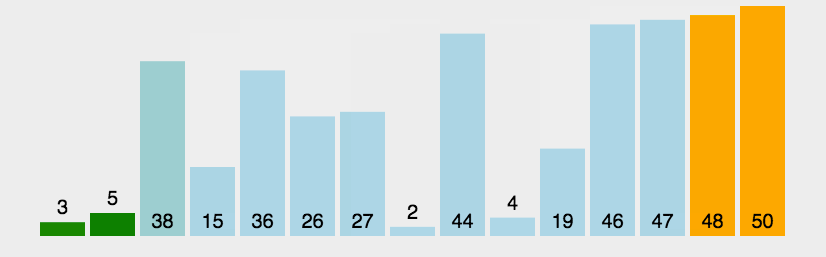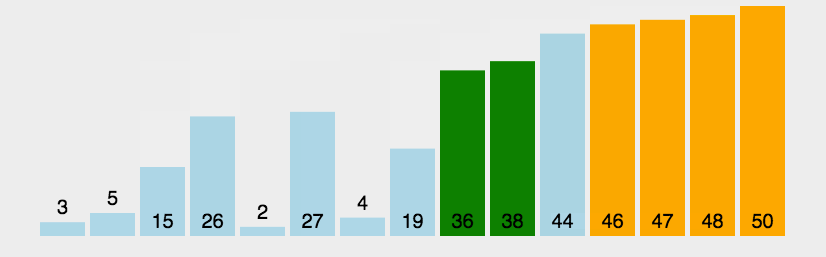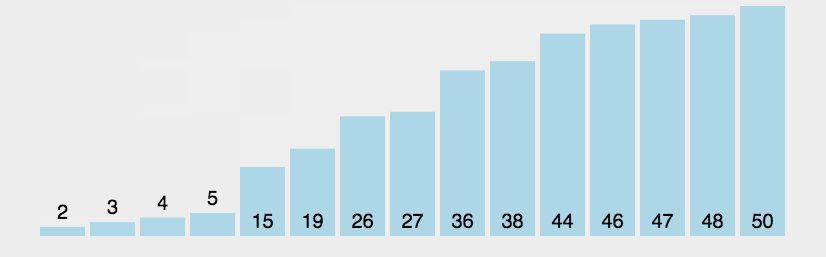
实现:
public static <T extends Comparable<T>> void bubbleSort(T[] data)
{
int position, scan;
T temp;
//循环次数为n-1,时间复杂度为O(n)
for (position = data.length - 1; position >= 0; position--)
{
//循环次数为n,时间复杂度为O(n)
for (scan = 0; scan <= position - 1; scan++)
{
if (data[scan].compareTo(data[scan+1]) > 0) {
swap(data, scan, scan + 1);
}
}
}
}
- 快速排序:以枢轴为基准,通过一趟排序,将待排元素分为左右两个子序列,左子序列元素的关键字均小于或等于枢轴元素的关键字,右子序列的关键字则大于枢轴元素的关键字;然后分别对两个子序列继续进行排序,直至整个序列有序。(递归)
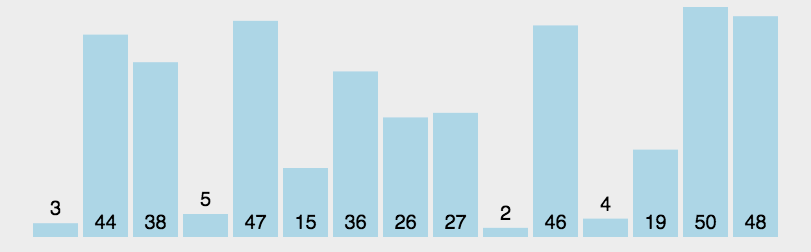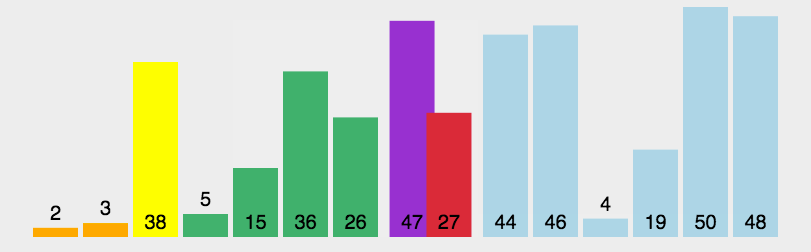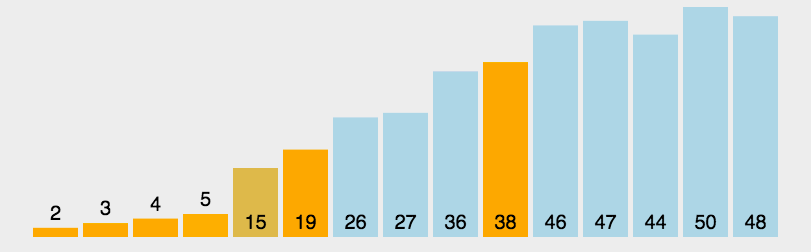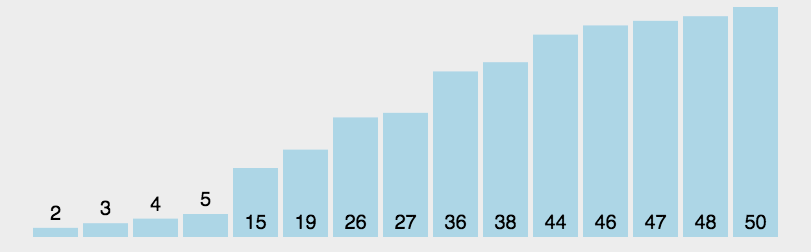
实现:
public class QuickSort {
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return;
}
i=low;
j=high;
temp = arr[low];
while (i<j) {
while (temp<=arr[j]&&i<j) {
j--;
}
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
3.选择排序
通过反复将某一特定值放到它在列表中的最终已排序位置来实现排序。
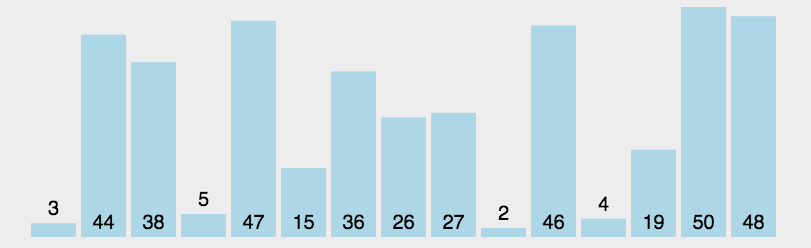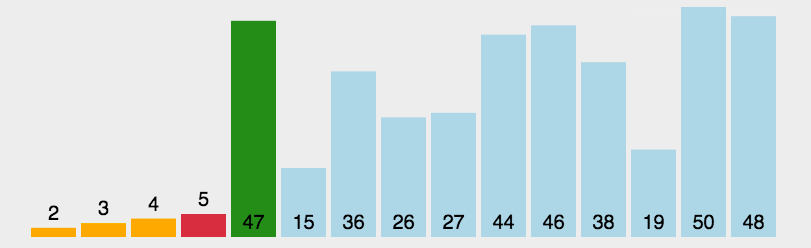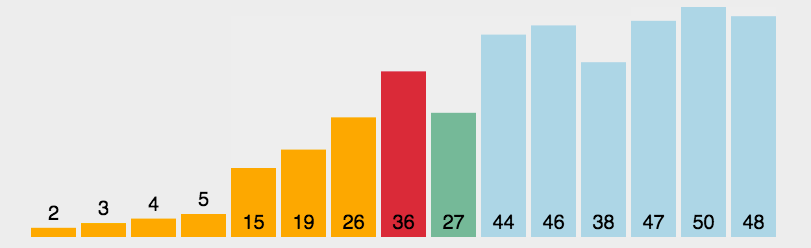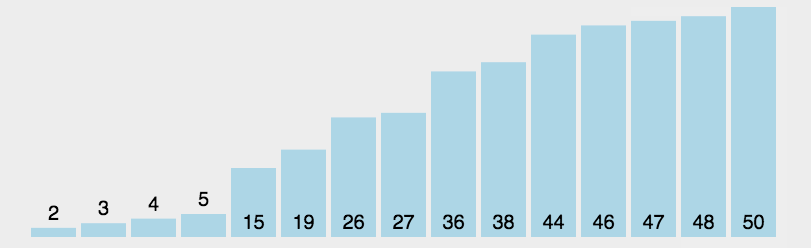
实现:
public static <T extends Comparable<T>> void selectionSort(T[] data)
{
int min;
T temp;
//循环次数为n,时间复杂度为O(n)
for (int index = 0; index < data.length-1; index++)
{
min = index;
//循环次数为n,时间复杂度为O(n)
for (int scan = index+1; scan < data.length; scan++) {
if (data[scan].compareTo(data[min])<0) {
min = scan;
}
}
swap(data, min, index);
}
}
4.基数排序:基于排序关键字结构来排序。

5.归并排序:通过将列表进行递归式分区直至最后每个列表中都只剩余一个元素后,将所有列表重新按顺序重组完成排序。

- 排序算法好坏衡量
- 时间效率:排序的时间开销可用算法执行中的数据比较次数与数据移动次数来衡量。
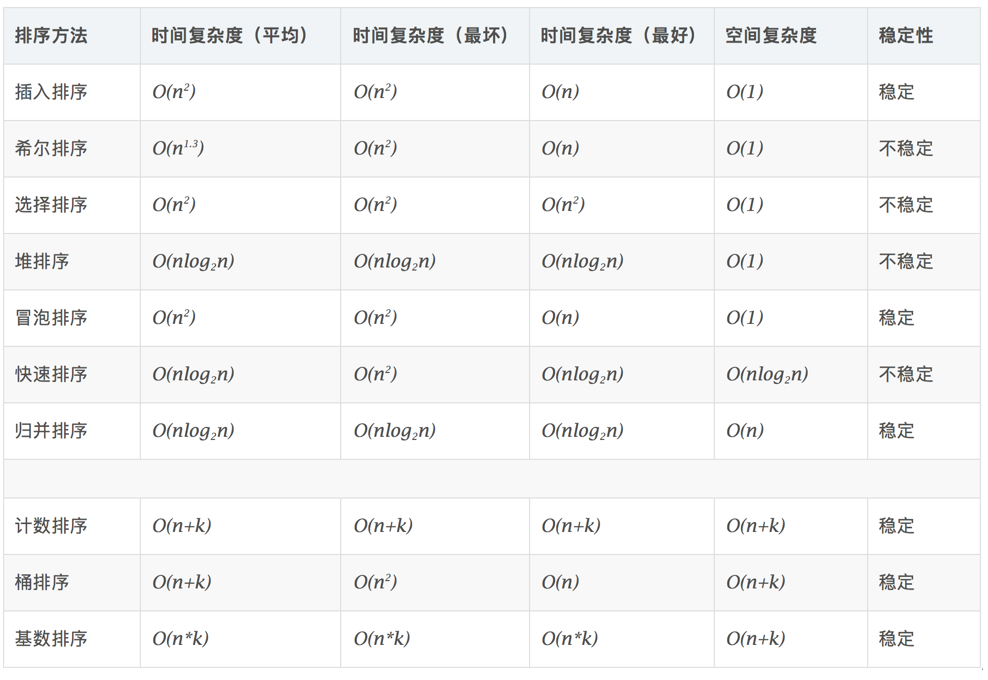
- 空间效率:占内存辅助空间的大小。
- 稳定度:若两个记录A和B的关键字值相等,但排序后A,B的先后次序保持不变,则可以说这种算法是稳定的。
教材学习中的问题和解决过程
- 问题1:快速排序算法逻辑及实现
- 问题1解决方案: 此处引用《啊哈!算法》中的形象讲解与可爱插图,但本书是用C语言实现,根据这个逻辑,用Java来实现(代码见教材学习内容)。
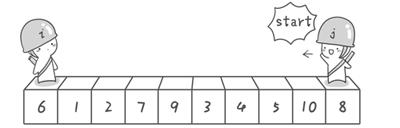
“6 1 2 7 9 3 4 5 10 8”
先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换它们。这里可以用两个变量i 和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i 指向序列的最左边(即i=1),指向数字6。让哨兵j 指向序列的最右边(即j=10),指向数字8。
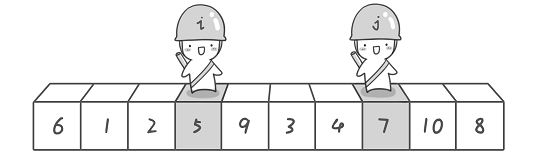
首先哨兵j 开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j 先出动,这一点非常重要。哨兵j 一步一步地向左挪动(即j–-),直到找到一个小于6的数停下来。接下来哨兵i 再一步一步向右挪动(即i++),直到找到一个大于6的数停下来。最后哨兵j 停在了数字5面前,哨兵i 停在了数字7面前。
现在交换哨兵i 和哨兵j 所指向的元素的值。交换之后的序列如下。
6 1 2 5 9 3 4 7 10 8
到此,第一次交换结束。接下来哨兵j 继续向左挪动(再次友情提醒,每次必须是哨兵j先出发)。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下。
6 1 2 5 4 3 9 7 10 8
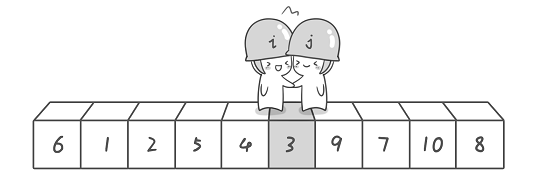
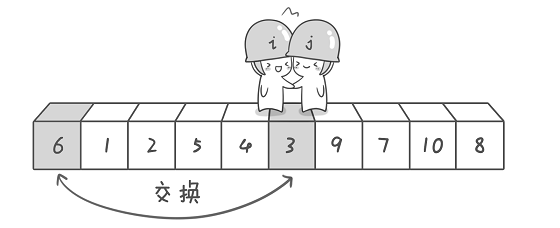
第二次交换结束,“探测”继续。哨兵j 继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下。
3 1 2 5 4 6 9 7 10 8
到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,其实哨兵j 的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6 为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。
代码调试中的问题和解决过程
-
问题1:
public static <T extends Comparable<T>> void method(T[] data)什么意思? -
问题1解决方案:
<T extends Comparable<? super T>>
extends的作用:extends后面跟的类型,如<任意字符 extends 类/接口>表示泛型的上限;
super的作用:与extends相反,表示的是泛型的下限。
即:extends对泛型上限进行了限制即T必须是Comparable<? super T>的子类,然后<? super T>表示Comparable<>中的类型下限为T。<T extends Comparable<T>>和<T extends Comparable<? super T>>有什么不同
<T extends Comparable<T>>
类型T必须实现Comparable接口,并且这个接口的类型是T。这样,T的实例之间才能相互比较大小。
<T extends Comparable<? super T>>
类型T必须实现Comparable接口,并且这个接口的类型是T或者是T的任一父类。这样声明后,T的实例之间和T的父类的实例之间可以相互比较大小。
代码托管

上周考试错题总结
无考试
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 254/254 | 2/2 | 21/21 | 开始编写简单的程序 |
| 第二周 | 132/386 | 1/3 | 26/47 | 学会使用Scanner类 |
| 第三周 | 632/1018 | 2/5 | 21/68 | 学会使用部分常用类 |
| 第四周 | 663/1681 | 2/7 | 27/95 | junit测试和编写类 |
| 第五周 | 1407/3088 | 2/9 | 30/125 | 继承以及继承相关类与关键词 |
| 第六周 | 2390/5478 | 1/10 | 25/150 | 面向对象三大属性&异常 |
| 第七周 | 1061/6539 | 2/12 | 25/175 | 算法,栈,队列,链表 |
| 第八周 | 813/7352 | 1/13 | 26/201 | 查找与排序 |
-
计划学习时间:25小时
-
实际学习时间:26小时