笔记:左偏树
摘要:贺了三道题,啥也没学会。
贺的是:hsfzLZH1 和 05年集训队论文 和 OI-wiki
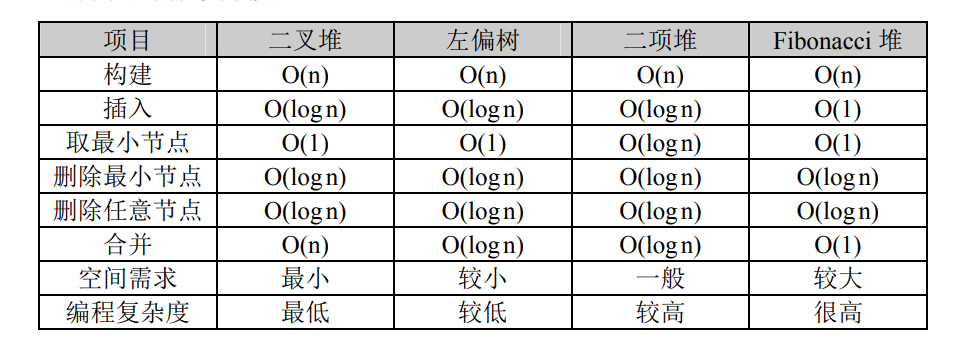
左偏树的定义和性质
我们定义一个 外节点 的 \(dis\) 是 1。每个点的 \(dis\) 等于它到最近的外节点的距离。特别地,空节点的 \(dis\) 是 -1。
那么,对于一个 \(n\) 个节点的二叉树,根的 \(dis\) 不超过 \(\log {(n+1)}-1\)。
Proof
一个根节点 \(dis\) 为 \(x\) 的二叉树,他至少有 \(x\) 层是满的。
\(n\ge 2^{x+1}-1\)
\(x\le \log {(n+1)}-1\)
左偏树,是一棵满足如下两个性质的二叉树。
两个性质:
- 具有左偏性质。即:\(\forall u\in T,dis(lson(u))\ge dis(rson(u))\)
- 具有堆性质。
两个结论:
- \(dis(u)=dis(rson(u))+1\)。下图是论文里的示例图。
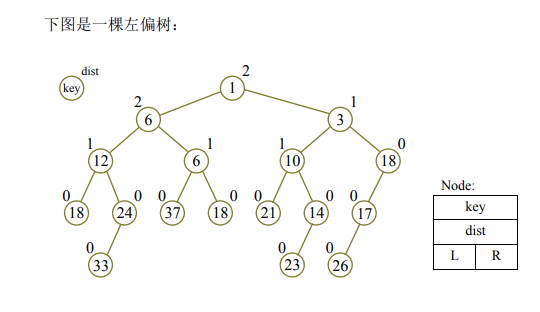
- 往右一直走,最多走 \(\log {(n+1)}-1\) 步
原因:对于一个 \(n\) 个节点的二叉树,根的 \(dis\) 不超过 \(\log {(n+1)}-1\)。
左偏树的操作
主要是合并,插入,删除根,建树,删除任意节点。
这里以小根堆为例。
合并
合并两棵左偏树。
把权值较大的左偏树 \(B\) 并到 根权值较小的的左偏树 \(A\) 的右子树 \(right(A)\) 上,一层层并下去。
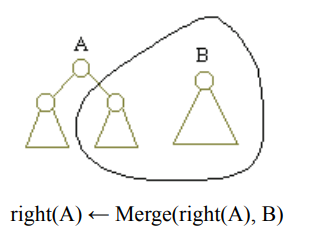
合并完了,这时候可能不再满足 \(dis(left(A))\ge dis(right(A))\),这时就交换 \(A\) 的左右子树。
(下图中第一次交换是为了保证 \(A\) 的根 比 \(B\) 的根 权值小)
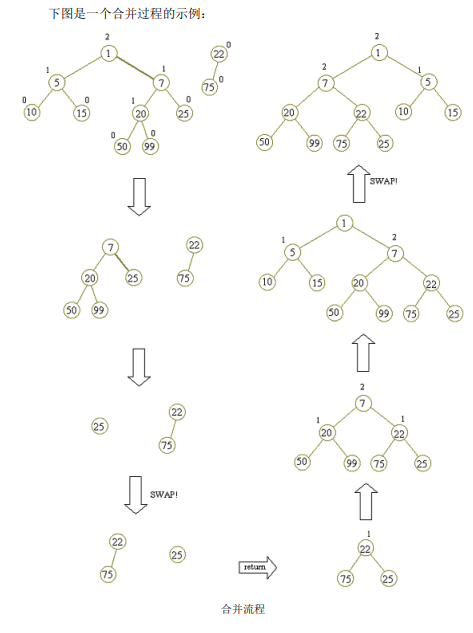
时间复杂度:每次向右走一步。\(O(\log n)\)
插入
直接将单点当做一棵树,执行合并操作。\(O(\log n)\)
删除根
合并俩儿子。\(O(\log n)\)
建树
下面都是论文的解释。


删除任意节点
下面都是OI wiki。
先将左右儿子合并,然后自底向上更新 、不满足左偏性质时交换左右儿子,当 \(dist\) 无需更新时结束递归:
int& rs(int x) { return t[x].ch[t[t[x].ch[1]].d < t[t[x].ch[0]].d]; }
// 有了 pushup,直接 merge 左右儿子就实现了删除节点并保持左偏性质
int merge(int x, int y) {
if (!x || !y) return x | y;
if (t[x].val < t[y].val) swap(x, y);
t[rs(x) = merge(rs(x), y)].fa = x;
pushup(x);
return x;
}
void pushup(int x) {
if (!x) return;
if (t[x].d != t[rs(x)].d + 1) {
t[x].d = t[rs(x)].d + 1;
pushup(t[x].fa);
}
}

习题
-
这真的适合当板题吗。。逐渐不会并查集的路径压缩。
code
#include<bits/stdc++.h> using namespace std; typedef long long ll; #define fi first #define se second #define mkp make_pair #define PII pair<int,int> const int N = 1e5 + 10; int n, m, f[N], val[N], dis[N], tr[N][2]; int find(int x) { return (x == f[x]) ? x : f[x] = find(f[x]); } int merge(int x, int y) { if(!x || !y) return x | y; if(val[x] > val[y] || (val[x] == val[y] && x > y)) swap(x, y); tr[x][1] = merge(tr[x][1], y); if(dis[tr[x][0]] < dis[tr[x][1]]) swap(tr[x][0], tr[x][1]); f[tr[x][0]] = f[tr[x][1]] = x; //最多也是跳log次。 dis[x] = dis[tr[x][1]] + 1; return x; } void del(int x) { val[x] = -1; f[tr[x][0]] = tr[x][0]; f[tr[x][1]] = tr[x][1]; f[x] = merge(tr[x][0], tr[x][1]); //子树中有些点路径压缩到的还是x,让他们跳到正确的根。 } int main() { dis[0] = -1; scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++) scanf("%d", &val[i]), f[i] = i; while(m--) { int op, x, y; scanf("%d", &op); if(op == 1) { scanf("%d%d", &x, &y); if(val[x] == -1 || val[y] == -1) continue; x = find(x); y = find(y); if(x != y) f[x] = f[y] = merge(x, y); } else { scanf("%d", &x); if(val[x] == -1) { puts("-1"); continue; } int y = find(x); printf("%d\n", val[y]); del(y); } } return 0; } -
是谁在贺自己以前的代码?是我啊,那没事了。
题意:给你一棵树(保证 \(fa_i<i\)),每个节点有val,lead。对于一个点,在它子树里选 \(\sum val \le m\) 的点,\(ans=max(ans,lead*tot)\) 。求最大ans
题解:
每个点维护一个堆,表示当前它子树中性价比最高且 \(\sum val \le m\) 的点。
从下到上遍历树(这里就直接从 \(n\) 扫到 \(1\)) 每次把该点的子树和它父亲当前子树合并。
每个点和父亲合并一次,被删除至多一次。\(O(\log n)\)
code
#include<bits/stdc++.h> using namespace std; typedef long long ll; #define fi first #define se second #define mkp make_pair #define PII pair<int,int> const int N = 1e5 + 10; int n, m, fa[N], tot[N], val[N], lead[N], dis[N], tr[N][2], rt[N]; ll sum[N]; int merge(int x, int y) { if(!x || !y) return x | y; if(val[x] < val[y]) swap(x, y); tr[x][1] = merge(tr[x][1], y); if(dis[tr[x][0]] < dis[tr[x][1]]) swap(tr[x][0], tr[x][1]); dis[x] = dis[tr[x][1]] + 1; return x; } int main() { dis[0] = -1; scanf("%d%d", &n, &m); ll ans = 0; for(int i = 1; i <= n; i++) { scanf("%d%d%d", &fa[i], &val[i], &lead[i]); rt[i] = i; sum[i] = val[i]; tot[i] = 1; ans = max(ans, 1ll * lead[i]); } for(int i = n; i > 1; i--) { sum[fa[i]] += sum[i]; tot[fa[i]] += tot[i]; rt[fa[i]] = merge(rt[fa[i]], rt[i]); while(sum[fa[i]] > m) { sum[fa[i]] -= val[rt[fa[i]]]; tot[fa[i]]--; rt[fa[i]] = merge(tr[rt[fa[i]]][0], tr[rt[fa[i]]][1]); } ans = max(ans, 1ll * lead[fa[i]] * tot[fa[i]]); } printf("%lld\n", ans); return 0; } -
论文题/yun
首先考虑将严格递增改成单调不降,\(b[i]-i\) 是单调不降序列。
不妨以 \(a[i]-i\) 作为 \(a\) 求单调不降的 \(b\),最后答案每个 \(+i\)
考虑特殊情况:
- 情况1:\(a\) 单调不降:\(a=b\)
- 情况2:\(a\) 单调不增:\(b_i\) 都是 \(a\) 中位数
考虑将原序列分成 \(m\) 段,每一段都是 情况2。(情况1 可以分裂成很多 情况2)
我们希望 \(b\) 递增,如果有相邻两段不递增,那么这一整段我们都取原来 \(a\) 数组里这一整段的中位数。Proof
设 \(a_{1}\) 到 \(a_n\) 中位数 为 \(u\),\(a_{n+1}\) 到 \(a_m\) 中位数是 \(v\),\(a_{1}\) 到 \(a_m\) 中位数是 \(w\)
现在的 \(b\) 是 \((u,u,...,u,v,v,...v)\)
如果 \(u\le v\),那很显然不用动了
如果 \(u>v\),我们要证明不存在答案比 \((w,w,w...w)\) 更优的 \(b\)
/ll 看论文吧。现在问题变成了:合并两个有序集以及查询某个有序集内的中位数。
我们发现,只有当某一区间内的中位数比后一区间内的中位数大时,合并操作才会发生,也就是说,任一区间与后面的区间合并后,该区间内的中位数不会变大。
于是我们可以用最大堆来维护每个区间内的中位数,当堆中的元素大于该区间内元素的一半时,删除堆顶元素,这样堆中的元素始终为区间内较小的一半元素,堆顶元素即为该区间内的中位数。
——论文
我们维护的堆,是前 \(\lceil \frac {len} 2\rceil\) 大的值。
使用左偏树,查询 \(O(1)\) ,合并 \(O(\log n)\)。 可以达到 \(O(n\log n)\) 的复杂度。code
#include<bits/stdc++.h> using namespace std; typedef long long ll; #define fi first #define se second #define mkp make_pair #define PII pair<int,int> const int N = 1e6 + 10; int n, m, dis[N], tr[N][2], val[N], a[N], b[N]; int top; struct node { int rt, l, r, sz, mid; node() { rt = 0; l = 0; r = 0; sz = 0; mid = 0; } node(int smrt, int sml, int smr, int smsz, int smmid) { rt = smrt; l = sml; r = smr; sz = smsz; mid = smmid; } }st[N]; int merge(int x, int y) { if(!x || !y) return x | y; if(val[x] < val[y]) swap(x, y); tr[x][1] = merge(tr[x][1], y); if(dis[tr[x][0]] < dis[tr[x][1]]) swap(tr[x][0], tr[x][1]); dis[x] = dis[tr[x][1]] + 1; return x; } int main() { dis[0] = -1; scanf("%d", &n); for(int i = 1; i <= n; i++) { scanf("%d", &a[i]); val[i] = a[i] - i; } for(int i = 1; i <= n; i++) { st[++top] = node(i, i, i, 1, a[i] - i); while(top > 1 && st[top - 1].mid > st[top].mid) { top--; st[top].r = st[top + 1].r; st[top].sz += st[top + 1].sz; st[top].rt = merge(st[top].rt, st[top + 1].rt); while(st[top].sz > (st[top].r - st[top].l + 2) / 2) { st[top].sz--; st[top].rt = merge(tr[st[top].rt][0], tr[st[top].rt][1]); } st[top].mid = val[st[top].rt]; } } for(int i = 1; i <= top; i++) for(int j = st[i].l; j <= st[i].r; j++) b[j] = st[i].mid + j; ll ans = 0; for(int i = 1; i <= n; i++) ans += abs(b[i] - a[i]); printf("%lld\n", ans); for(int i = 1; i <= n; i++) printf("%d ", b[i]); puts(""); return 0; } /* 5 2 5 46 12 1 */

