LOJ #2880,BZOJ 4237,LG AT1225 「JOISC 2014 Day3」稻草人

かかしかかしかかしかかしかかしかかしかかしかかしかかしかかしかかし

如果不用关心组成的矩形里面有没有其他稻草人，就可以直接二维数点了，可惜不行，那么我们考虑cdq分治。（我也不知道为什么是这样转化）
不妨按y分治，最后的数组是归并排序成 \(x\) 升序的。

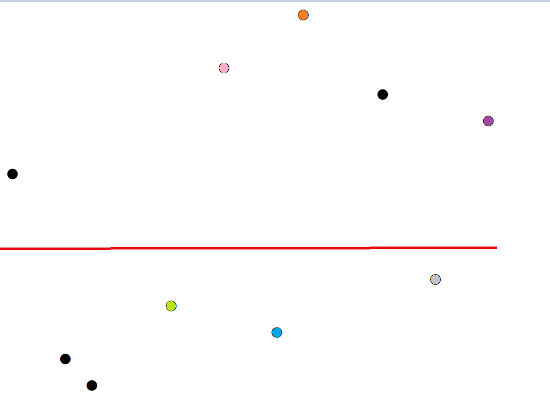
如果在同一个边，那就继续分治
如果不在同一边，怎么计算？
不妨在扫右上角的点的时候统计答案。
设当前扫到的右上角的点（在上半边）是 \((x_b,y_b)\) 合法的左下角点（在下半边）是 \(x_a,y_a\)。
我们最后的数组是归并成 \(x\) 升序的，所以我们扫到的点都是 \(x\) 递增的。
一对点对受到了两种限制，上半边和下半边。

• 上半边的限制
  \(x_a<x_c<x_b,y_a<y_c<y_b\) 的 \((x_a,y_a)\) 不能存在。（\(a,b\) 组成的矩形中间有点）
  我们扫过的所有点正是 \(y_a<y_c,x_c<x_b\) 的所有点（\(b\) 左下的点），那么就是要求 \(\forall y_c<y_b,x_a> x_c\)
  也就是 \(x_a \ge max\{x_c | y_c<y_b\}\)。（图中，如果以橙点为 \(b\)，那么由于粉点的影响，\(a\) 可以是蓝点，但不可以是绿点。）
  所以维护一个 \(y\) 单调递增的单调栈，用于找到左边最近的（即 \(x_c\) 最大） \(y_c<y_b\) 就可以了。
• 下半边的限制
  \(x_a<x_c<x_b,y_a<y_c<y_b\) 的 \((x_a,y_a)\) 不能存在。（\(a,b\) 组成的矩形中间有点）
  我们扫过的所有点正是 \(y_a<y_c,x_c<x_b\) 的所有点（\(b\) 左下的点），那么就是要求 \(\forall x_a<x_c,y_a>y_c\)
  其实就是任意满足 \(x_1<x_2\) 两点的，必须同时满足 \(y_1>y_2\)（图中，如果以紫点为 \(b\)，那么\(a\) 可以是灰点，但不可以是绿点和蓝点。）
  所以维护一个 \(y\) 单调递减的单调栈。栈内就是 \(x\) 递增，\(y\) 递减的了。

然后每次统计答案的时候，二分单调栈即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ls(x) ((x)<<1)
#define rs(x) ((x)<<1|1)
#define fi first
#define se second
#define mkp make_pair
#define PII pair<int,int>
int read() {
    char c = getchar(); int ff = 1; int x = 0;
    while(c < '0' || c > '9') { if(c == '-') ff = -1; c = getchar(); }
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return ff * x;
}
const int N = 2e5 + 10;
int n, lshx[N], lshy[N], lenx, leny; ll ans;
struct node {
	int x, y;
	friend bool operator < (node &a, node &b) {
		return a.y < b.y;
	} 
}p[N], tmp[N];
int st1[N], st2[N];
bool cmp(int a, int b) { return p[a].x < p[b].x; }
void cdq(int l, int r) {
	
	if(l == r) return;
	int mid = (l + r) >> 1;
	cdq(l, mid); cdq(mid + 1, r);
	//st1：x单调递增，维护y单调递减。（如果该点能贡献，那么在下半部分内它右上角且横坐标x之前的地方，没点。即任意贡献点，x1<x2,y1>y2） 
	//st2: x单调递增，找左边第一个满足y'<y的，维护y单调递增。 
	int i = l, j = mid + 1, k = l - 1, top1 = 0, top2 = 0;
	while(i <= mid || j <= r) {
		if(j > r || (i <= mid && p[i].x < p[j].x)) {
			while(top1 && p[st1[top1]].y < p[i].y) top1--;
			tmp[++k] = p[i]; st1[++top1] = i; i++;
		} else {
			while(top2 && p[st2[top2]].y > p[j].y) top2--; 
			
			p[n + 1].x = p[n + 1].y = 0; if(top2) p[n + 1].x = p[st2[top2]].x;
			int pos = lower_bound(st1 + 1, st1 + top1 + 1, n + 1, cmp) - st1;
			ans += top1 - pos + 1; 
			tmp[++k] = p[j]; st2[++top2] = j; j++;
		}
	}
	for(int i = l; i <= r; i++) p[i] = tmp[i];

	return;
}
int main() {
//	freopen("ex.out", "w", stdout);
	n = read();
	for(int i = 1; i <= n; i++) {
		p[i].x = read(), p[i].y = read();
		lshx[++lenx] = p[i].x, lshy[++leny] = p[i].y;
	}
	sort(lshx + 1, lshx + lenx + 1); sort(lshy + 1, lshy + leny + 1);
	for(int i = 1; i <= n; i++) {
		p[i].x = lower_bound(lshx + 1, lshx + lenx + 1, p[i].x) - lshx;
		p[i].y = lower_bound(lshy + 1, lshy + leny + 1, p[i].y) - lshy;
	}
	sort(p + 1, p + n + 1);
	cdq(1, n);
	printf("%lld\n", ans);
	return 0;
}