2021初赛:毒瘤汇总
已经加入了2020年的毒瘤汇总。
杂
链接器的功能是( B)。
把源代码转换成特定硬件平台的机器指令。
把机器指令组合成完整的可执行程序。
把源代码转换成可执行程序。
把高级语言翻译成低级语言。
-
世界上第一次提出「人工智能」这⼀概念的科学家是(C )
A. 艾伦·麦席森·图灵(Alan Mathison Turing)
B. 冯·诺伊曼(John von Neumann)
C. 约翰·麦卡锡(John McCarthy)
D. 斯蒂芬·威廉·霍金(Stephen William Hawking) -
编译器的作用是(D)
A. 把源代码转换成特定硬件平台的机器指令
B. 把机器指令组合成完整的可执行程序
C. 把源代码转换成可执行程序
D. 把高级语言翻译成低级语言
11、下列排序算法中最好最坏情况下的时间复杂度相同的是(C)。
A、希尔排序 O(n)~O(nlogn)
B、快速排序 O()~O(n^2)
C、堆排序 O(nlogn)
D、基数排序 O(nk) k会变!!
12、下列关于说法正确的是(B)。
A、贪心算法不具有最优子结构性质
B、动态规划全局最优解一定包含局部最优解
C、动态规划可以不满足无后效性
D、贪心算法的子问题往往互相独立
2.下列不属于应用层协议的是(D)。
A. FTP协议 B.HTTP协议 C.SMTP协议 D.TCP协议
12、以下在OSI模型中不属于TCP/IP模型中的应用层的是(BC)
A、会话层 B、网络层
C、数据链路层 D、表示层
13.下列哪些算法是由tarjan发明的(ABC)
A、Splay
B、LCT
C、Median of medians linear time selection algorithm
D、Timsort
9、请给以下四个事件发生的时间排序(B)
1.举办第一次NOIP
2.举办第一次NOI网络同步赛
3.NOIP提高组由四题改为三题
4.举办第一次APIO
A、1234 B、1243
C、2134 D、2143
以下是面向对象的高级语言的有(BD )。
A. 汇编语言
B. C++
C. Fortran
D. Java
面向过程:C,BASIC,Pascal;
面向对象:C++,Java,Smalltalk,Object Pascal ,Python;
解释型语言(java,Python)
7.下列有关CPU的说法,正确的是( B )
A.CPU的用途是将计算机系统所需要的显示信息进行转换驱动显示器。
B.CPU 的性能和速度取决于时钟频率(一般以赫兹或千兆赫兹计算,即 hz 与 Ghz)和每周期可处理的指令(IPC),两者合并起来就是每秒可处理的指令(IPS)。
C.AMD 是世界上最大的半导体公司,也是首家推出 x86 架构处理器的公司。
D.目前的 CPU 一般都带有3D 画面运算和图形加速功能,所以也叫做“图形加速器”或“3D加速器”。
解析:A、D都是显卡,C是INTEL
7、下列地址中,属于B类IP地址的是(C )。
A、27.33.119.2 B、192.97.32.121 C、133.201.189.32 D、126.33.82.107
是128.0.0.0~191.255.255.255
4、真正能唯一标识出一台计算机网络中一台计算机的地址是(D)。
A.地址掩码
B.ip地址
C.域名地址
D.MAC地址
选D 不是B
mac地址是是网卡芯片的唯一标识码
一个网卡会有一个全球唯一固定的MAC地址,但可对应多个IP地址。
域名地址,域名与IP对应,一个域名可以对应多个IP,一个IP可以对应多个域名
10.若要使用 g++ 编译器,开启 -Ofast 优化,且使用 C++ 11 标准,将源文件 prog.cpp 编译为可执行程序 exec,且保留调试信息,则需要使用的编译命令为( D )
A.g++ prog.cpp -Ofast exec -std=c++11 -debug
B.g++ prog.cpp -Ofast exec -std=c++11 -g
C.g++ prog.cpp -o exec -Ofast -std=c++11 -debug
D.g++ prog.cpp -o exec -Ofast -std=c++11 -g

1、采样频率为44.1kHz,16位量化的双声道立体声,其20秒钟数据量约为(C)。
A)1.68MB B)1.68KB
C)3.36MB D)3.36KB
44.1*1000*2*20*16/8*1024*1024=C
2、在下列几种存储器中,访问速度最快的是(D)。
A.硬盘 B.cache C.RAM D.寄存器
寄存器>Cache>RAM>ROM>u盘
15、下列关于高级语言的说法不正确的是(C)。
A、Fortran是历史上的第一个面向科学计算的高级语言
B、Pascal和C都是编译执行的高级语言
C、BASIC是历史上的第一个支持面向对象的语言
D、编译器将高级语言程序转变为目标代码
历史上的第一个支持面向对象的语言是Simula 67
数值转换、逻辑运算
2、以下四项中( A )项与别的选项最不相同。
A.P∧﹁ Q
B.(P ∧ Q)→ P
C.P →( P ∨ Q)
D.﹁( P ∨ Q)∨﹁( ﹁P ∧ ﹁Q)
A是可满足式,其它都是重言式
16、令p,q,r,s为四个命题,判定下列命题的可满足性(可满足定义为存在一组(p,q,r,s)使命题为真)。其中可满足的有(AD)
A、(p ∨ ¬q) ∧ (¬p ∨ q) ∧ (¬p ∨ ¬q)
B、(p → q) ∧ (p → ¬q) ∧ (¬p → q) ∧ (¬p → ¬q)
C、(p ↔ q) ∧ (¬p ↔ q)
D、(p ∨ q ∨ ¬r)∧(p ∨ ¬q ∨ ¬s)∧(p ∨ ¬r ∨ ¬s)∧(¬p ∨ ¬q ∨ ¬s) ∧ (p ∨ q ∨ ¬s)
1、与二进制数101.01011等值的十六进制数为(D)。
A.A.B B.5.51 C.A.51 D.5.58
补0啊白痴
数学
- 两艘轮船都要停靠同一个泊位,它们可能在昼夜的任意时刻到达,甲、乙两船停靠泊位的时间分别为4小时和2小时,求有一艘船停靠泊位时必须等待一段时间的概率。
A、29/144 B、67/288
C、35/144 D、55/288
https://zhidao.baidu.com/question/1925193434845790827.html
- 在一条长度为 1 的线段上随机取两个点,则以这两个点为端点的线段的期望长度是(B)。
A. 1 / 2
B. 1 / 3
C. 2 / 3
D. 3 / 5
https://blog.csdn.net/Hi_KER/article/details/83040154
5、已知2018年10月7日是星期日,那么1296年8月17日是(C)
A. 星期一 B.星期二
C.星期五 D.星期六
17xx年的时候某人-10天了。
麻蛋,算了半天。
14、\(有三个1级分裂怪,每个x级怪可以吃掉另x-1到x+1个x级怪\)
\(分裂出x^2 - 1 到 x^2+2个x + 1级分裂怪(自己死亡),\)
\(求以下哪几种怪的个数情形是可能出现的?\)ABCD
A、0个一级分裂怪,1个二级分裂怪,6个三级分裂怪,10个四级分裂怪
B、2个一级分裂怪,3个三级分裂怪,3个4级分裂怪,35个5级分裂怪
C、1个一级分裂怪,2个三级分裂怪,3个4级分裂怪,46个5级分裂怪
D、3个一级分裂怪
10、随机抛硬币,在连续三次得到的结果是正反正时停止。那么期望抛的次数是(D)
A、7 B、8
C、9 D、10
10、桌上有若干枚棋子,甲、乙两人玩轮流取棋子游戏,每次可取1枚、3枚或4枚,但不可取2枚,当无棋子取时算输。甲、乙两人都是玩取棋子游戏的绝顶高手,从不会失误。现甲、乙两人共玩了三局,先手分别是,甲,乙,甲,三局游戏开始时棋子枚数分别是7,13,21。问甲、乙双方在三局游戏中的必胜方分别是(C)?
A.乙 乙 甲 B. 甲 乙 甲
C.乙 乙 乙 D. 乙 甲 乙
后取必胜.
设先取为甲,后取为乙
则每轮乙取的数必须与甲取的数,两数之和能被3整除.
即甲取1,则乙取2;甲取2则乙取4;甲取4则乙取2.
因16被3除余1,如此取法,可使最终必余一数给甲.
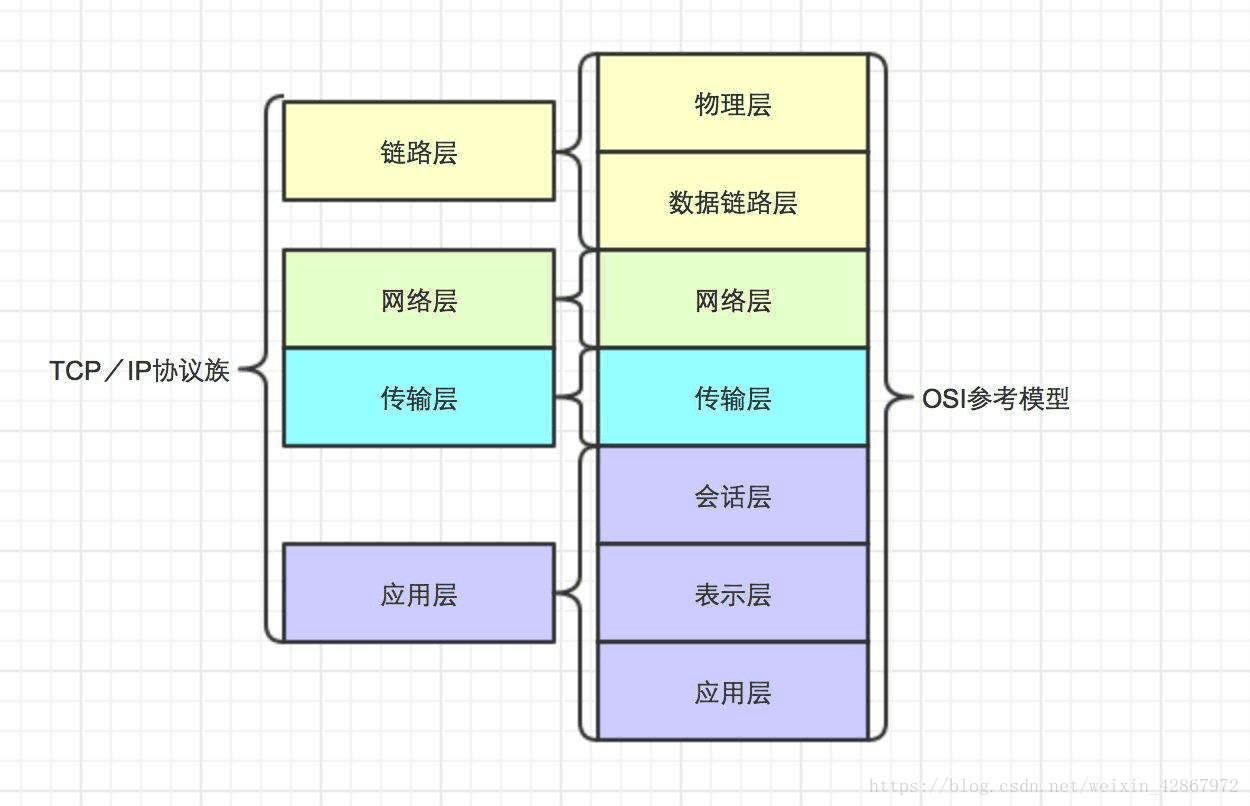
10、给定如图所示的正方形(n=3)。我们可以在这个正方形的某个格子上放置大炮。但是,如果大炮在同一行或者同一列,他们就会互相攻击到。大炮数量为2,请你求出可能的放置方案总数,使得大炮互相不会攻击到。现在告诉你n=3时,总数为46,则n=4时,总数为()。
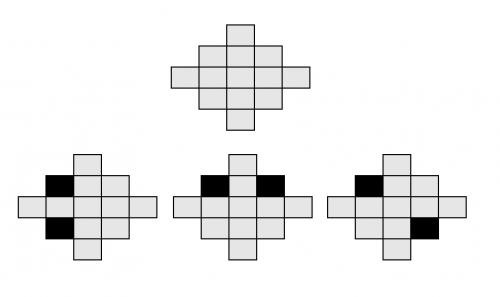
如图所示:上面为n=3的正方形,下面三幅图,前两幅可以互相攻击到,第三幅无法互相攻击到。
A、127 B、157 C、206 D、248
解析:首先注意n=4的正方形不要画错(长为4宽为4)。
考虑到限制条件为不同行不同列,那么我们可以做一个等价变换:
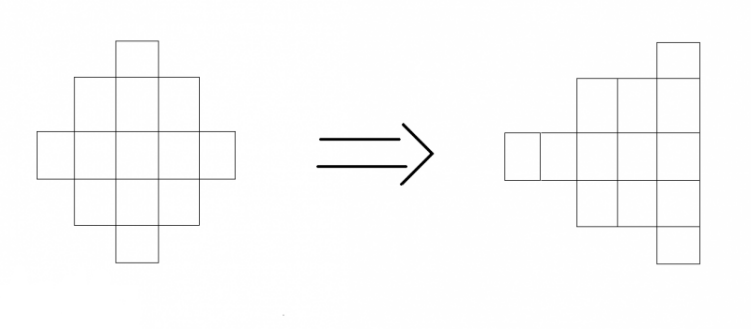
把原图变为一个宽度递增的图形,这样做的好处是避免了后效性问题。
设f[i][k]表示前i列放了k个的方案,
有f[i][k]=f[i−1][k]+f[i−1][k−1]∗(lon[i]−(k−1)) lon(i)表示当前列的宽度
15.在xxy的面前摆了4包不同品牌的薯条(用a代替)和5包不同品牌的蕃茄酱(用b代替),其中有4个b的品牌与4个a一一对应,另一个b的品牌则无法对应。每次操作,xxy从剩下的a中随机选择一个,从剩下的b中随机选择一个,一起吃掉。这样4此以后,a已经没有了,b还有一包,xxy就会把这包b送给小y。问xxy恰好只吃到一组同品牌的a和b的概率约为( A )
A. 37% B. 36% C. 33% D. 31%
解析:分两种清况。
第一种,抛弃的b刚好是多余品牌。那么选一对a,b对应正确,其余错排即可。4*2
第二种,选一对a,b对应正确,再选一个a对应多余b。剩余两个可简单列出。 总的433
\((4*2+4*3*3)/P(5,4)\)
13、Kathy函数是这样定义的:
f(1)=1
f(3)=3
f(2n)=f(n)
f(4n+1)=2f(2n+1)-f(n)
f(4n+3)=3f(2n+1)-2f(n)
对于一个给定的数m=55,求出所有满足f(n)=n,(n<=m)的自然数n的个数(B )
A. 11 B. 13 C. 17 D. 25
解析:m以内,二进制编码形态下是回文串的个数。
3、一个圆形水池中等概率随机分布着四只鸭子,那么存在一条直径,使得鸭子全在直径一侧的概率是(D)。
A.1/16 B.1/8 C.A.1/4 D.1/2
考虑首先固定一只鸭子,这只鸭子与圆心的连线将圆分为两部分。
那么剩下的 3 只鸭子都在同一个半圆的概率为\((\frac{1}{2})^3\times 2=0.25\)。
如果令顺时针方向的半圆有效的话,概率就是 0.125 。而 4 只鸭子是独立的,所以总的概率是 0.5 。
4、工厂里有三根铁棒,分别长为 3,4,5,现在你可以对其中一些铁棒进行加长,但总的加长长度不能超过10,问有多少种加长的方案使得加长后的铁棒可以构成三角形。( A )
A.187 B. 274 C.286 D. 572
答案是187
枚举加长长度i,那么总方案为\(\sum C(i,2)\) 插板法。
然后再减去非法的方案:非法方案计算也是插板法。
具体见XJOI 8835
11、S是集合{1,2,…,2004}的子集,S中的任意两个数的差不等于4或7,S中最多含有多少个元素?(D)
A.840
B.835
C.910
D.912

1 5 9 2 6 10 3 7 11 4 8 1
时间复杂度
11、T(n)为某个算法输入为n时的运算次数。如果T(i)(i<=1)为常数,且T(n)=3T(sqrt(n))+log2n,那么以下比T(n)复杂度低有(AC)
A、O(log(n)*sqrt(log(n)) B、O(sqrt(n))
C、O(log(n)) D、O(log^2(n))
若某算法的计算时间表示为递推关系式:
T(N) = 2T(N / 2) + N log N
T(1) = 1
则该算法的时间复杂度为( )。
A. \(O(N)\)
B. \(O(N \log N)\)
C. \(O(N \log^2 N)\)
D. \(O(N^2)\)
正确答案: C
利用分叉树来做,根结点nlogn,每次下分两个子树,结点为n/2logn/2,一直做到最后,发现最后的log里面的真数为1,也就是0。对每一层加和,第一层nlogn,第二层nlogn/2也就是nlogn-nlog2,以此类推,nlogn-nlog4,nlogn-nlog8,....,nlogn-nlogn。树高以2为底logn,乘进去为nlognlogn - n/2logn -n/2*(logn)2,就是O(n(logn)2)。(手机百度回答不会插入图片,我是这么做的,有错误还请指出
9、以下关于渐进记号的性质是正确的有:()
A.f(n) =Θ(g(n)),g(n) =Θ(h(n)) ⇒f(n) =Θ(h(n))
B.f(n) =O(g(n)),g(n) =O(h(n)) ⇒h(n) =O(f(n))
C.O(f(n))+O(g(n)) = O(min{f(n),g(n)})
D.f(n) = O(g(n)) ⇔g(n) = O(f(n))
算法分析中,记号O表示渐进上界,记号Ω表示渐进下界,记号Θ表示紧渐进界
11、设有向图有n个顶点和e条边,采用邻接表作为其存储表示,在进行拓扑排序时,总的计算时间为( B )。
A. O(nloge) B. O(n+e) C. O(ne) D. O(n^2)
???
5、建堆算法可以用递推式表示:把建堆过程想成先对左子树建堆(T(n/2)),再对右子树建堆(T(n/2)),最后对根下溯(O(lg n)),可得:
T(n) = 2*T(n/2) + O(lg n)
求T(n)时间复杂度( C )。
A.O (n^2) B.O (n logn ) C.O (n) D. O (1)
设 \(n = 2^k\)

树、图
8、一棵二叉树的高度为h(根为第一层),所有节点的度为0或2,则此树最少有()个节点。
A、 2^h-1 B、2h-1 C、2h+1 D、h+1
B
4、一张10个点的完全图,任意删去一条边,它的哈密顿回路的数量为(A)
A、141120 B、322560
C、161280 D、362880
边:可以a-b和b-a
/2:1231 和1321 重复了。
6、设完全图G有n个结点,m条边,则当(C)时,G中存在欧拉回路。
A.m为奇数 B.m为偶数 C.n为奇数 D.n为偶数
7、有n个叶子的哈夫曼树的结点总数为( D )
A.不确定 B.2n C.2n+1 D.2n-1
14、下列有关图的说法不正确的是(B)。
A.用边表示活动的网络(AOE网)的关键路径是指从源点到终点的路径长度最长的路径。
B.对于AOE网络,加速任一关键活动就能使整个工程提前完成。
C.对于AOE网络,任一关键活动延迟将导致整个工程延迟完成。
D.在AOE网络中,可能同时存在几条关键路径,称所有关键路径都需通过的有向边为桥。
阅读程序
1、
1 #include<bits/stdc++.h>
2 using namespace std;
3 int arr[101];
4 int main() {
5 int n,gap;
6 cin>>n;
7 for(int i=1; i<=n; i++)
8 cin>>arr[i];
9 for (gap = n / 2; gap > 0; gap /= 2){
10 int k=0;
11 for (int i = gap; i <= n; i++){
12 for (int j= i - gap; j > 0 && arr[j] > arr[j + gap]; j -= gap){
13 swap(arr[j], arr[j + gap]);
14 k++;
15 }
16 }
17 cout<<k<<endl;
18 }
19 for(int i=1; i<=n; i++)
20 cout<<arr[i]<<" ";
21 return 0;
22 }
17、若gap恒为1,20行输出结果不变。( T )
2、
1 struct Node {
2 ll d,id;
3 bool operator < (const Node &A) const {
4 return d > A.d);
5 }
6 };priority_queue<Node> pq;
7 inline void f() {
8 for(int i=1; i<=n; i++) dis[i]=inf/3;
9 dis[1]=0,pq.push((Node) {0,1});
10 while(!pq.empty()) {
11 Node now=pq.top();
12 pq.pop();
13 int val=now.d,u=now.id;
14 if(dis[u]<val) continue;
15 for(int p=head[u]; p; p=nxt[p]) {
16 int v=a[p];
17 if(dis[u]+b[p]<dis[v]) {
18 dis[v]=dis[u]+b[p];
19 pq.push((Node) {dis[v],v});
20 }
21 }
22 }
23 }
23、对于任意输入,17行b[p]的值一定不能小于0。( T )
3、
如下代码用来计算字符串s的前缀函数。
定义前缀函数pi[i]=max(k=0-i){k:s[0…k-1]=s[i-(k-1)…i]}
简单来说pi[i]就是,子串s[0…i]最长的相等的真前缀与真后缀的长度。
例如:s[0…4]=ababc,pi[3]=2,pi[4]=0
规定:单个字符没有真前缀和真后缀,pi[0]=0
1 vector<int> prefix_function(string s) {
2 int n = (int)s.length();
3 vector<int> pi(n);
4 for (int i = 1; i < n; i++) {
5 int j = pi[i - 1];
6 while (j > 0 && s[i] != s[j]) j = pi[j - 1];
7 if (s[i] == s[j]) j++;
8 pi[i] = j;
9 }
10 return pi;
11 }
28、该算法是在线算法。( T )
29、pi数组中元素值域为[0,n)。( F )
1、
1 #include
2 using namespace std;
3 void fun(char *a, char b, int &c) {
4 a = b;
5 (a)++;
6 c++;
7 }
8 int main() {
9 char c1, c2, *p1, *p2;
10 c1 = 'A';
11 c2 = 'a';
12 int c3;
13 c3 = 48;
14 p1 = &c1;
15 p2 = &c2;
16 fun(p1, p2, c3);
17 cout << c1 <<" "<< c2 <<" "<< c3 << endl;
18 return 0;
19 }
16、第3行和第14行的‘&’含义相同。( F )
分别是引用和指针!!
完善程序
2【好数】对于一个正整数X,如果把X化成二进制数后,如果X的二进制数至少有三个连续的1或者至少有3个连续的0(不能有前导0),那么X就是“好数”。例如8就是“好数”,因为8对应的二进制数是1000,有三个连续的0。整数15也是“好数”,因为15对应的二进制数是1111,也有三个连续的1。整数27就不是“好数”,因为27对应的二进制数是11011,既没有连续的三个1也没有连续三个0。
现在给出两个整数Low、UP,求Low和UP范围内有多少个“好数”。(0 <= Low <= UP <= 2147483647)
代码如下:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll F[125][2][2];
ll Ans,Sum,len,k,n,m;
string sm;
ll Change(ll t) {
if(t<=0)return 0;
Ans=0,k=t,len=0;
sm="";
while(k) { //求t的二进制
char s=k%2+48;
sm=s+sm,k/=2;
}
len=sm.length();
for(int i=2; i<len; ++i) //求t的二进制长度-1位的坏数
Ans+= ① ;
if(t>0) ② ;
k=0;//求t的二进制长度位的坏数
while(++k<=len)
if(sm[k]=='1') {
sm[k]='0';
int l=1;
char r=sm[0];
bool B=0;
for(int i=1; i<=k; ++i)
if( ③ ) {
l++;
if(l==3) {
B=1;
break;
};
} else l=1,r=sm[i];
if(B==0)
Ans+= ④ ;
sm[k]='1';
}
int l=1;
char r=sm[1];
bool B=0;
for(int i=2; i<=len; ++i)
if( ⑤ ) {
l++;
if(l==3) {
B=1;
break;
};
} else l=1,r=sm[i];
if(!B)Ans++;
return t-Ans;
}
int main() {
scanf("%d%d",&n,&m);
F[2][1][0]=F[2][1][1]=F[2][0][0]=F[2][0][1]=1;//初值
for(int i=3; i<=31; ++i) {
F[i][0][0]=F[i-1][0][1];
F[i][1][0]= ⑥;
F[i][1][1]=F[i-1][1][0];
F[i][0][1]= ⑦;
}
Sum=Change(m)-Change(n-1);//前缀和
printf("%d",Sum);
return 0;
}
39.填入①处的代码是 C
A. F[i-1][1][0]+F[i-1][1][1]
B. F[i-1][0][1]+F[i-1][1][1]
C. F[i][1][0]+F[i][1][1]
D. F[i][0][1]+F[i][1][1]
40.填入②的代码是 B
A.len++
B. Ans++
C. F[0][0][0]
D. F[1][0][0]
41.填入③⑤处的代码是 A
A. sm[i]==r
B. sm[i]==’0’
C. sm[i]==’1’
D. sm[i]==sm[k]
42.填入④处的代码是 D
A. F[len-k][sm[k]-48][0]
B. F[len-k][sm[k-1]-48][0]
C. F[len-k+1][sm[k]-48][0]
D. F[len-k+1][sm[k-1]-48][0]
43.填入⑥和⑦处的代码分别是 D
A. F[i-1][1][1];F[i-1][0][1]
B. F[i-1][0][1];F[i-1][1][1]
C. F[i-1][1][1]+F[i-1][0][1];F[i-1][0][1]+F[i-1][1][0]
D. F[i-1][0][0]+F[i-1][0][1];F[i-1][1][1]+F[i-1][1][0]

 2021初赛:毒瘤汇总
2021初赛:毒瘤汇总


