二维计算几何基础
感觉写这个总是怀疑自己数学是不是完蛋了
以下全为抄各种课件
建议看WC2022课件。
自己的混乱板子 code
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
double eps = 1e-8, inf = 1e15, Pi = acos(-1.0);
const int N = 200010;
int dcmp(double x) {
if(fabs(x) < eps) return 0;
return (x < 0) ? -1 : 1;
}
struct Point {
double x, y;
Point() { x = y = 0; }
Point(double a, double b) { x = a; y = b; }
friend Point operator + (Point a, Point b) { return Point(a.x + b.x, a.y + b.y); }
friend Point operator - (Point a, Point b) { return Point(a.x - b.x, a.y - b.y); }
friend Point operator * (Point a, double b) { return Point(a.x * b, a.y * b); }
friend Point operator / (Point a, double b) { return Point(a.x / b, a.y / b); }
friend bool operator == (Point a, Point b) { return (dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0); }
bool operator < (const Point a) const {
return (x != a.x) ? (x < a.x) : (y < a.y);
}
Point turn(Point p0, double ang) {
Point p = Point(x, y);
Point tmp = (p - p0);
tmp.x = tmp.x * cos(ang) - tmp.y * sin(ang);
tmp.y = tmp.y * sin(ang) + tmp.y * cos(ang);
return p0 + tmp;
}
};
typedef Point Vector;
struct Line {
//l=(1-t)A+tB=A+t(B-A)=x+ty
Point p; Vector v;
Line() { p.x = p.y = v.x = v.y = 0; }
Line(Point a, Point b) { p = a; v = b - a; }
};
double Dot(Point a, Point b) { return a.x * b.x + a.y * b.y; }
double Cross(Point a, Point b) { return a.x * b.y - a.y * b.x; }
double Len(Point a) { return sqrt(a.x * a.x + a.y * a.y); }
double LineProjection(Point p, Point p1, Point p2) { return Dot(p - p1, p2 - p1) / Len(p2 - p1); }
Point ProjectionPoint(Point p, Point p1, Point p2) { return p1 + (p2 - p1) * LineProjection(p, p1, p2) / Len(p2 - p1); }
Point ReflectionPoint(Point p, Point p1, Point p2) { return ProjectionPoint(p, p1, p2) * 2 - p; }
void Clockwise(Point p, Point p1, Point p2) {
double cr = Cross(p1 - p, p2 - p);
if(cr) {
if(cr > 0) puts("COUNTER_CLOCKWISE");
else puts("CLOCKWISE");
} else {
double lp = LineProjection(p, p1, p2);
if(lp < 0) puts("ONLINE_BACK");
else if(lp - Len(p2 - p1) > 0) puts("ONLINE_FRONT");
else puts("ON_SEGMENT");
}
}
bool isOnSegment(Point p, Point p1, Point p2) {
//若允许在点与端点重合
if(p == p1 || p == p2) return 1;
return (dcmp(Cross(p1 - p, p2 - p)) == 0 && dcmp(Dot(p1 - p, p2 - p)) < 0);
//若不允许点与端点重合
//return (Len(P - A) + Len(B - P) - Len(B - A) == 0);
}
void LinePO(Line l1, Line l2) {
if(Cross(l1.v, l2.v) == 0) puts("2");
else if(Dot(l1.v, l2.v) == 0) puts("1");
else puts("0");
}
int SegmentProperIntersection(Line l1, Line l2) {
Point a1 = l1.p, a2 = l1.p + l1.v, b1 = l2.p, b2 = l2.p + l2.v;
//若不允许在端点处相交,删去下一行
if(isOnSegment(a1, b1, b2) || isOnSegment(a2, b1, b2) || isOnSegment(b1, a1, a2) || isOnSegment(b2, a1, a2)) return 1;
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1);
double c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
//cout<<(dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0)<<endl;
return (dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0);
}
Point LineIntersection(Line a, Line b) {
Point p = a.p, q = b.p;
Vector v = a.v, w = b.v, u = p - q;
double t = Cross(w, u) / Cross(v, w);
return p + v * t;
}
double DistanceToLine(Point a, Line b) {
Point b1 = b.p, b2 = b.p + b.v;
Point t = ProjectionPoint(a, b1, b2);
return Len(a - t);
}
double DistanceToSeg(Point a, Line b) {
Point b1 = b.p, b2 = b.p + b.v;
Point t = ProjectionPoint(a, b1, b2);
if(!isOnSegment(t, b1, b2)) return inf;
return Len(a - t);
}
double SegmentDistance(Line a, Line b) {
if(SegmentProperIntersection(a, b)) return 0;
Point a1 = a.p, a2 = a.p + a.v, b1 = b.p, b2 = b.p + b.v;
double x = min(min(DistanceToSeg(a1, b), DistanceToSeg(a2, b)), min(DistanceToSeg(b2, a), DistanceToSeg(b1, a)));
double y = min(min(Len(a1 - b1), Len(a1 - b2)), min(Len(a2 - b1), Len(a2 - b2)));
return min(x, y);
}
double PolygonArea(int n, Point *p) {
double ret = 0;
for(int i = 2; i <= n; i++)
ret += Cross(p[i] - p[1], p[(i + 1 > n) ? 1 : (i + 1)] - p[1]);
return fabs(ret) / 2;
}
int isConvex(int n, Point *p) {
p[n + 1] = p[1]; p[n + 2] = p[2];
for(int i = 1; i <= n; i++)
if(Cross(p[i] - p[i + 1], p[i + 2] - p[i + 1]) > 0) return 0;
return 1;
}
int PointinPolygon(Point p0, int n, Point *p) {
//cout<<"calc:"<<endl;
p[n + 1] = p[1];
for(int i = 1; i <= n; i++)
if(isOnSegment(p0, p[i], p[i + 1])) return 1;
int cnt = 0;
for(int i = 1; i <= n; i++) {
Point a = p[i], b = p[i + 1];
if(a.y > b.y) swap(a, b);
if(dcmp(Cross(a - p0, b - p0)) < 0 && dcmp(a.y - p0.y) < 0 && dcmp(p0.y - b.y) <= 0)
cnt++;
}
if(cnt & 1) return 2;
return 0;
}
void ConvexHull(int n, Point *p, int &m, Point *q) {
sort(p + 1, p + n + 1);
m = 0;
for(int i = 1; i <= n; i++) {
while(m > 1 && Cross(p[i] - q[m], q[m - 1] - q[m]) >= 0) m--;
q[++m] = p[i];
}
int k = m;
for(int i = n - 1; i >= 1; i--) {
while(m > k && Cross(p[i] - q[m], q[m - 1] - q[m]) >= 0) m--;
q[++m] = p[i];
}
if(p[0] == p[m] && n > 1) m--;
return;
}
double squaredist(Point a) {
// cout<<a.x<<" "<<a.y<<endl;
return a.x * a.x + a.y * a.y;
}
double MaxDistConvex(int n, Point *p) {
if(n == 1) return 0;
if(n == 2) return squaredist(p[2] - p[1]);
double ans = 0;
p[n + 1] = p[1];
int j = 2, bg = 2;
for(int i = 1; i <= n; i++) {
//对于边(p[i], p[i+1])
while(dcmp(fabs(Cross(p[j] - p[i], p[i + 1] - p[i])) - fabs(Cross(p[j % n + 1] - p[i], p[i + 1] - p[i]))) <= 0) {
if(j == bg) break;
ans = max(ans, max(squaredist(p[j] - p[i]), squaredist(p[j] - p[i + 1])));
j = j % n + 1;
}
if(i == 1) bg = i;
ans = max(ans, max(squaredist(p[j] - p[i]), squaredist(p[j] - p[i + 1])));
ans = max(ans, squaredist(p[i] - p[i + 1]));
}
return sqrt(ans);
}
code
//误差分析
int dcmp(double x) {
static double eps = 1e-8;
return (x > eps) - (x < -eps);
}
struct Point;
typedef Point Vector;
struct Point{
double x, y;
void in() {
scanf("%lf%lf", &x, &y);
}
void print() {
printf("%.2lf %.2lf\n", x, y);
}
Point(double x = 0, double y = 0) : x(x), y(y) {
}
//坐标旋转
inline Vector rotate(double ang) {
return Vector(x * cos(ang) - y * sin(ang), x * sin(ang) + y * cos(ang));
}
inline double dot(const Vector &a) {
return x * a.x + y * a.y;
}
inline bool operator == (const Point &a) const {
return sgn(x - a.x) == 0 && sgn(y - a.y) == 0;
}
inline bool operator < (const Point &a) const {
return sgn(x - a.x) < 0 || sgn(x - a.x) == 0 && sgn(y - a.y) < 0;
}
inline Vector operator + (const Vector &a) const {
return Vector(x + a.x, y + a.y);
}
inline Vector operator - (const Vector &a) const {
return Vector(x - a.x, y - a.y);
}
//叉积
inline double operator * (const Vector &a) const {
return x * a.y - y * a.x;
}
inline Vector operator * (double t) const {
return Vector(x * t, y * t);
}
inline Vector operator / (double t) {
return Vector(x / t, y / t);
}
inline double vlen() {
return sqrt(x * x + y * y);
}
inline Vector norm() {
return Point(-y, x);
}
};
//直线相交
point intersect(point P, Vector v, point Q, Vector w) {
point p;
Vector u = P - Q;
double t = (w * u) / (v * w);
p = P + v * t;
return p;
}
//凸包
void gao(){
if(n < 3){
return;
}
std::sort(p, p + n);
std::copy(p, p + n - 1, p + n);
std::reverse(p + n, p + 2 * n - 1);
int m = 0, top = 0;
for(int i = 0; i < 2 * n - 1; i++) {
while(top >= m + 2 && sgn((p[top - 1] - p[top - 2]) * (p[i] - p[top - 2])) <= 0) {
top--;
}
p[top++] = p[i];
if(i == n - 1) {
m = top - 1;
}
}
n = top - 1;
}
//半平面交
int inhalfplane(point p,point s,point e) {
return sgn((e - s) * (p - s)) ;
}
std::vector<point> CUT(const std::vector<point> &p, point s, point e) {
//p: 当前维护的凸包,s: 加入直线的起点, e: 加入直线的终点
//可用的一侧平面在直线左侧。
//分类讨论可推导出。
std::vector<point> q;
int n = (int) p.size();
for(int i = 0; i < n; i++) {
int nowin = inhalfplane(p[i], s, e);
int nextin = inhalfplane(p[(i + 1) % n], s, e);
if(nowin >= 0) {
q.push_back(p[i]);
}
if(nextin * nowin < 0) {
q.push_back(intersect(p[i], p[(i + 1) % n] - p[i], s, e - s));
}
}
return q;
}
//多边形判断是否在内部
bool point_in_polygon(Point o, Point *p, int n) {
int t;
Point a, b;
p[n] = p[0];
for(int i = 0; i < n; i++) {
if(dot_on_seg(o, Seg(p[i], p[i + 1]))) {
return true;
}
}
t = 0;
for(int i = 0; i < n; i++) {
a = p[i]; b = p[i + 1];
if(a.y > b.y) {
std::swap(a, b);
}
if(sgn((a - o) * (b - o)) < 0 && sgn(a.y - o.y) < 0 && sgn(o.y - b.y) <= 0) {
t++;
}
}
return t & 1;
}
基础知识
向量
点 \(A(x_1,y_1)\) 指向 \(B(x_2,y_2)\) 的向量为 \((x_2-x_1,y_2-y_1)\)
一个向量可以表示两个点之间的方向,以及长度
点积(内积)
两个向量 \(A,B\) 做点积等价于 \(x_1*x_2+y_1*y_2=|A||B|*cos(\theta)\)
点积也用来求两个向量的夹角
还可以用来求一个向量在另一个向量上的投影
叉积(外积)
两个向量 \(A(x_1,y_1), B(x_2,y_2)\) 的叉积可以表示为 \(x_1*y_2-x_2*y_1\)
叉积的值如果为正,表示从B向量在A向量的左边;如果为负,表示B向量在A向量的右边。
即假设A,B向量都从原点O出发,那么 从OA到OB如果在顺时针180度范围内,叉积就为正,否则为负
坐标旋转
点 \((x_1, y_1)\) 以 \((x_0, y_0)\) 为中心逆时针旋转 \(a\) 度
等价于 \((x_1-x_0, y_1-y_0)\) 绕原点旋转,求出旋转后的坐标加上 \((x_0,y_0)\) 即可
\((x,y)\) 绕原点逆时针旋转 \(a\) 度会得到
\((x*cos(a) - y * sin(a), x*sin(a) + y * cos(a))\)
距离
原坐标系的曼哈顿距离,就等于将每个点 \((x,y)\) 都转成 \((x+y,x-y)\) 下的切比雪夫距离。
原坐标系的切比雪夫距离,就等于将每个点 \((x,y)\) 都转成 \((\frac {x+y} 2,\frac {x-y} 2)\) 下的曼哈顿距离。
曼哈顿距离坐标系是由切比雪夫坐标系旋转 45°,再缩小到原来的一半得到的(?)
多边形
求多边形的面积(不一定是凸的):随便按照一个方向求相邻 三个点构成的有向三角形的面积之和, 最后取绝对值
\(O(\log n)\) 判断点是否在凸多边形内部:二分判断点在哪一块三角形区域内,最后再判断点是否在三角形内部
存储
- 点
记录其横纵坐标值即可。用 pair 或开结构体记录均可。 - 向量
由于向量的坐标表示与点相同,所以只需要像点一样存向量即可(当然点不是向量)。 - 线
- 直线与射线
直线上一点和直线的方向向量。 - 线段
只需要记录左右端点即可。
- 直线与射线
- 多边形
开数组按一定顺序记录多边形的每个顶点即可。 - 曲线
一些特殊曲线,如函数图像等一般记录其解析式。对于圆,直接记录其圆心和半径即可
凸包与半平面交
凸包
常见求凸包的方法有两种:水平序和极角序
水平序是先求下凸折线,再求上凸折线,最后拼成凸包
极角序是选择一个左下角的点当作原点,所有的点按照 与原点连线后跟x轴正向的角度 排序(此处可以学一下atan2函数)
排序之后的操作都差不多,下面以水平序为例
凸包的思想也经常用于其它与单调性有关的算法中,比如斜率优化
将凸包分成上下两条凸折线
用一个栈记录折线上的点,假设栈顶的元素为b,前一个为a
假设当前点为c
如果 \(cross(a, b, c) \ge 0\) 则直接将c加入栈中
否则将b退栈,直到 \(cross(a,b,c) \ge 0\)
半平面交
有若干个 \(ax+by+c = 0\) 的直线, 每个直线有一侧是我们需要的一个半平面,求所有半平面的交集(一个凸多边形)
有 \(n^2\) 与 \(n\log n\) 两种做法
此处介绍 \(n^2\) 做法
维护一个凸包,表示半平面的交,
每次新来一条直线,暴力找到这条直线会与哪条凸包上的边相交(如果某条边两个端点在直线的异侧,肯定有交点)
然后求出新的交点,维护新的凸包
\(n\log n\) 的算法使用双端队列优化,可参考刘汝佳训练指南
点、直线/线段、圆、多边形之间关系
判断点是否在线段上
判断点 \(Q\) 在线段 \(P_1P_2\) 上:
- \((Q-P_1)\times (P_2-P_1)=0\)
- Q 在以 \(P1,P2\) 为对角顶点的矩形内。
判断两线段是否相交
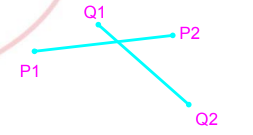
- 快速排斥试验
- 设以线段 P1P2 为对角线的矩形为R, 设以线段 Q1Q2 为对角线的矩形为T,如果R和
T不相交,显然两线段不会相交。
- 跨立实验
- 如果两线段相交,则两线段必然相互跨立对方。
- 若P1P2跨立Q1Q2 ,则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧.
- 即 \(( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0\)
- 上式可改写成 \(( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0\) 。
- 故判断P1P2跨立Q1Q2的依据是:\(( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) \ge 0\)
计算点到线段的最近点
分平行于 \(x\) 轴/ \(y\) 轴 、 不平行(线段斜率不为0/不存在)的情况讨论
计算点到圆的最近距离及交点坐标
分P为O、PO平行于 \(x\) 轴/ \(y\) 轴 、 PO不平行(线段斜率不为0/不存在)的情况讨论
计算线段/直线与圆的交点坐标
设圆心为O,圆半径为r,直线(或线段)L上的两点为P1,P2。
-
如果L是线段且P1,P2都包含在圆O内,则没有交点;否则进行下一步。
-
如果L平行于Y轴,
-
a) 计算圆心到L的距离dis;
-
b) 如果dis > r 则L和圆没有交点;
-
c) 利用勾股定理,可以求出两交点坐标,但要注意考虑L和圆的相切情况。
-
-
如果L平行于X轴,做法与L平行于Y轴的情况类似;
-
如果L既不平行X轴也不平行Y轴,可以求出L的斜率K,然后列出L的点 斜式方程,和圆方程联立即可求解出L和圆的两个交点;
-
如果L是线段,对于2,3,4中求出的交点还要分别判断是否属于该线段的范围内
直线求交
求两直线交点需要先判断是否平行或者共线
求交点时可以利用参数方程来做
将第一条直线上的点表示成 \((P.x+v.x * t_1, P.y + v.y * t_1)\) 的形式
将第二条直线上的点表示成 \((Q.x+w.x*t_2,Q.y+w.y * t_2)\) 的形式
两项分别相等可以解出 \(t_1\) 和 \(t_2\),就可以求出交点
求线段交点可以先求直线交点 再判断交点是否在线段上
判断点在多边形内
判断点在任意多边形内部:射线法,做一条线,判断与多边形相交几次,奇数次就表示在多边形内部,否则在外
- 对于多边形的水平边不作考虑;
- 对于多边形的顶点和L相交的情况,如果该顶点是其所属的边上纵坐标较大的顶点,则计数,否则忽略;
- 对于P在多边形边上的情形,直接可判断P属于多边形。
判断线段在多边形内
- 线段的两个端点都在多边形内 。
- 线段不和多边形的边内交。如果线段和多边形的某条边内交 ,则线段一定会有一部分在多边形外(内交:两线段相交且交点不在两线段的端点).
- 求出所有和线段相交的多边形的顶点。按照X为第一关键字,Y为第二关键字将坐标排序,这样相邻的两个点就是在线段上相邻的两交点,如果任意相邻两点的中点也在多边形内,则该线段一定在多边形内。

 二维计算几何基础
二维计算几何基础

