字符串板子
宁就是板子集结大师? 人很难受,然后devinwang在讲烤馍片,然后开始copy代码。
最小表示法
gugugu
字符串哈希
子串哈希 O(1)
\(hash=hash_{r}-hash_{l-1}base^{r-l+1}\)
证明:
\(hash(1,r)=\sum_{i=1}^r \sum a_ibase^{r-i}\)
\(hash(1,l-1)=\sum_{i=1}^{l-1} \sum a_ibase^{l-1-i}\)
\(hash(l,r)=\sum_{i=l}^r \sum a_ibase^{r-i}\)
\(hash(l,r)=\sum_{i=1}^r \sum a_ibase^{r-i}-\sum_{i=1}^{l-1} \sum a_ibase^{r-i}\)
\(hash(l,r)=hash(1,r)-\sum_{i=1}^{l-1} \sum a_ibase^{l-1-i}base^{r-l+1}\)
\(hash(l,r)=hash(1,r)-hash(1,l-1)base^{r-l+1}\)
void pre(){
p[0]=1;f[0]=0;
for(int i=1;i<=n;i++){
f[i]=(1ll*f[i-1]*bs+s[i]-'a')%mod;
p[i]=1ll*p[i-1]*bs%mod;
}
}
int calc(int l,int r){
return ((f[r]-1ll*f[l-1]*p[r-l+1]%mod)%mod+mod)%mod;
}
KMP
输出在 \(s1\) 中所有出现的 \(s2\) 的位置
定义一个字符串 \(s\) 的border 为一个非 \(s\) 的子串 \(t\) ,满足 \(t\) 既是 \(s\) 的前缀,又是 \(s\) 的后缀。
输出 \(s2\) 的每个前缀 \(s'\) 的最长border的长度。(实际上就是反悔操作)
char s1[N],s2[N];
int p[N],n,m;
void pre(){
int j=0;p[1]=0;
for(int i=2;i<=n;i++) {
while(j>0&&s2[j+1]!=s2[i]) j=p[j];
if(s2[j+1]==s2[i]) j++;
p[i]=j;
}
return;
}
void kmp(){
int j=0;
for(int i=1;i<=n;i++) {
while(j>0&&s2[j+1]!=s1[i]) j=p[j];
if(s2[j+1]==s1[i]) j++;
if(j==m){
printf("%d\n",i-m+1);
j=p[j];
}
}
return;
}
int main(){
scanf("%s",s1+1);scanf("%s",s2+1);
m=strlen(s2+1),n=strlen(s1+1);
pre();kmp();
for(int i=1;i<=m;i++)
printf("%d ",p[i]);
return 0;
}
字典树
这就不写了吧草,这是一个01 trie的应用。
void ins(ll x, int val){
int p = 1;
for(int i = 60; i >= 0; i--){
sum[p] = (sum[p] + val) % mod;
int c = ((x >> i) & 1);
if(!ch[p][c]) ch[p][c] = ++sz;
p = ch[p][c];
}
if(p) sum[p] = (sum[p] + val) % mod;
return;
}
int query(ll x){
int p = 1, ret = 0;
for(int i = 60; i >= 0; i--){
int c = ((x >> i) & 1);
if((X >> i) & 1) p = ch[p][c ^ 1];
else ret = (ret + sum[ch[p][c ^ 1]]) % mod, p = ch[p][c];
if(!p) break;
}
if(p) ret = (ret + sum[p]) % mod;
return ret;
}
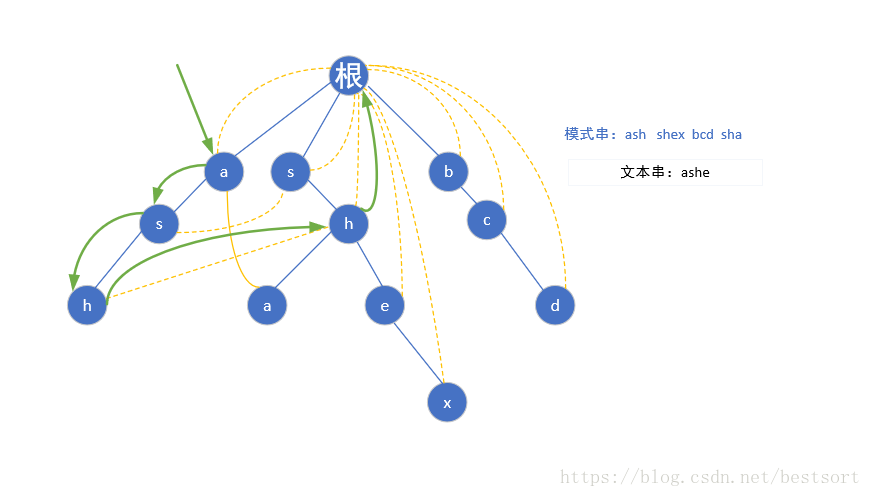
AC自动机
和著名的某张图。注意e不是结束节点
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n, cnt=0, tr[N][30], tot[N], fail[N];
char ch[N], t[N];
void insert(char* s){
int len = strlen(s+1);
int p = 0;
for(int i = 1; i <= len; i++){
int c=s[i] - 'a';
if(!tr[p][c]) tr[p][c] = ++cnt;
p=tr[p][c];
}
tot[p]++;
}
void getfail(){
queue<int>q;
for(int c = 0; c < 26; c++)
if(tr[0][c]) fail[tr[0][c]] = 0, q.push(tr[0][c]);
while(!q.empty()){
int p = q.front(); q.pop();
for(int c = 0; c < 26; c++){
if(tr[p][c]) fail[tr[p][c]] = tr[fail[p]][c], q.push(tr[p][c]);
else tr[p][c] = tr[fail[p]][c];
}
}
}
int query(char* s){
int p = 0, ret = 0, len = strlen(s+1);
for(int i = 1; i <= len; i++){
int c = s[i] - 'a';
p = tr[p][c];
for(int j = p; j && tot[j] != -1; j = fail[j])
ret += tot[j], tot[j] = -1;
}
return ret;
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%s",ch+1);
insert(ch);
}
fail[0] = 0; getfail();
scanf("%s",t + 1);
printf("%d\n", query(t));
return 0;
}
Manacher
update:现在习惯全用 # 并判边界
Oh how confused this konjac is! It is tring to write down some notes to help itself!
给出一个字符串 S ,求 S 中最长回文串的长度 。
-
朴素算法是以每一个点和间隔为中点往外扫。时间复杂度 \(O(n^2)\)
-
马拉车算法 时间复杂度 \(O(n)\)
首先,构造一个字符串 \(s2\) ,将字符串 \(s1\) 的尾以及间隔处插入 #,头部插入$
如果s1=aaa,则s2=$a#a#a#
这样做的效果是把所有回文串对应到了一个奇回文串上,将对接下来的操作有帮助。
设一个数组 \(p_i\) 表示第 \(i\) 个字符的回文半径。
例如 $#a#b#c#b#a#a#b#c#b#a# 其中第一个c的回文串就是#a#b#c#b#a#
回文半径就是6。
如何用 \(p_{1...i-1}\) 推出 \(p_i\) ?
设 \(mx\) 为当前最大回文串右边界, \(id\) 为当前最大回文串对称中心。
则 \(mx=id+p[id]\)
我们先求出以 \(i\)为中心的回文半径至少有多长。
- i<mx 时:
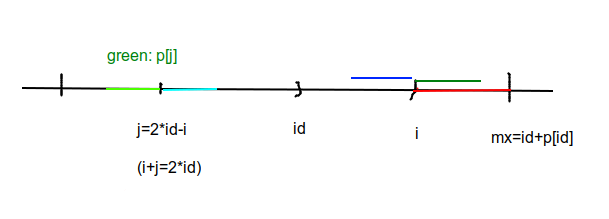
\(p_i\) 的值可以通过 \(p_j\) 转移而来,因为左右是关于id对称的。也就是说,深蓝=浅蓝,深绿=浅绿。需要注意的是,\(mx-i\) 可能会 \(<p_j\) 此时 \(p_i=mx-i\)
所以 \(p_i=min(p_{2*id-i},mx-i)\)
- i>mx 时,直接先设 \(p_i=1\)。
之后再往两遍扩展即可。求出 \(p_i\) 后要更新 \(mx\) 和 \(id\) 。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=11e6+10;
int n,p[N<<1];
char s1[N],s2[N<<1];
int manacher(){
int tot=0;
s2[tot++]='$',s2[tot++]='#';
for(int i=1;i<=n;i++)
s2[tot++]=s1[i],s2[tot++]='#';
tot--;
int mxlen=0,mx=0,id=0;
for(int i=1;i<=tot;i++){
if(i<mx) p[i]=min(p[id*2-i],mx-i);
else p[i]=1;
while(s2[i-p[i]]==s2[i+p[i]]) p[i]++;
if(mx<i+p[i]) mx=i+p[i],id=i;
mxlen=max(mxlen,p[i]-1);
}
return mxlen;
}
int main(){
scanf("%s",s1+1);
n=strlen(s1+1);
printf("%d\n",manacher());
return 0;
}
SA
看下那篇09年国集论文就是。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
const int N = 1e6 + 10;
char s[N];
int n, m, rk[N], sa[N], y[N], cnt[N], tmp[N], h[N];
void Sort() {
for(int i = 1; i <= m; i++) cnt[i] = 0;
for(int i = 1; i <= n; i++) cnt[rk[i]]++;
for(int i = 2; i <= m; i++) cnt[i] += cnt[i - 1];
for(int i = n; i >= 1; i--)
sa[cnt[rk[y[i]]]--] = y[i];
}
void get_sa() {
m = 127;
for(int i = 1; i <= n; i++)
rk[i] = s[i], y[i] = i;
Sort();
for(int w = 1; w <= n; w <<= 1) {
int len = 0;
for(int i = n - w + 1; i <= n; i++) y[++len] = i;
for(int i = 1; i <= n; i++)
if(sa[i] > w) y[++len] = sa[i] - w;
Sort();
swap(tmp, rk); m = 1; rk[sa[1]] = 1;
for(int i = 2; i <= n; i++) {
if(tmp[sa[i - 1]] != tmp[sa[i]] || tmp[sa[i - 1] + w] != tmp[sa[i] + w])
m++;
rk[sa[i]] = m;
}
}
}
void get_hi() {
int k = 0;
for(int i = 1; i <= n; i++) {
if(rk[i] == 1) continue;
int j = sa[rk[i] - 1]; if(k) k--;
while(i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
h[rk[i]] = k;
}
}
int main(){
scanf("%s", s + 1); n = strlen(s + 1);
get_sa();
int ans = 0;
for(int i = 1; i <= n; i++)
printf("%d ", sa[i]);
puts("");
return 0;
}
/*
aabaaaab
JSOI07
*/
SAM
写的乱七八糟,待填坑

 字符串板子
字符串板子